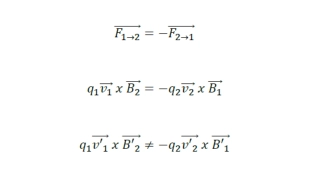Indian Contributions to General Relativity Post-Independence Era
Indian scholars have made significant contributions to the field of General Relativity post-independence, focusing on important problems like Big Bang singularity, gravitational collapse, black holes, gravitational waves, and quantum aspects. Notable achievements include AKR's Raychaudhury Equation, Hoyle-Narlikar theory, Senovilla's singularity-free solutions, and research on gravitational collapse and naked singularities. These efforts have advanced cosmology and our understanding of the dynamics of the universe.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
GR Research: Indian Contributions Post Independence Era Within the limitations of my understanding and perception I would attempt to review the important contributions. Let me apologize at the outset to who think their contributions were important but I might have missed them.
Important Problems Big - Bang Singularity Gravitational Collapse Black Holes Gravitational waves GR and Beyond Quantum Aspects Exact Solutions
BIG - BANG: COSMOLOGY AKR: Raychaudhury Equation governing dynamics of the Universe. Perhaps the most important equation that inspired the famous Singularity theorems. Undoubtedly the most outstanding contribution to GR. JVN: Hoyle - Narlikar theory - new theory of gravitation. A brilliant attempt of incorporating Mach s Principle. Unfortunately supported observationally unfavoured Steady State Cosmology.
Cosmology Senovilla: Singularity Free Solutions - cylindrical LK Patel, RS Tikekar, ND, & AKR, ND - spherical AKR: Attempted to formulate criterion for singularity free models by asking space time averages of matter distribution should vanish. Following that Senovilla has recently proposed positivity of energy is respected globally only on the average;i.e. With Violation allowed locally he claims to have succeeded in what AKR had conjectured. A criterion for non-occurrence of Big Bang Singularity.
Gravitational Collapse Datt (1938), Oppenheimer Snyder (1939) homogeneous collapse AKR: Unaware of the earlier work rediscovered D-OS collapse matching it with exterior empty space which was not done by D-OS. Singularity theorems and Penrose s conjecture Of no naked singularity always covered by horizon.
Gravitational Collapse Attempts to prove or disprove Penrose s conjecture, constructing models. Christodoulou in 1983 raised the first doubt that inhomogeneous collapse may lead to NS Can a null ray come out from singularity before formation of apparent horizon? Could you take back a null ray to end at the singularity? PSJ: It is the latter that has been mastered. A large number of examples of NS have been worked out by him and his collaborators, and also by large number of university workers.
Naked Singularity Joshi and Dwivedi showed that there exists enough choice in the initial data for BH & NS. Shear plays determining role, (PSJ, Rituparna, Roy, ND) GRBs birth cries of BHs (Roy, PSJ, ND) Question: Could we bring out a null ray emanating from NS? Field is diverging there, photon should get trapped, they shouldn t be able to come out or infinitely red-shifted!
Black Holes Schwarzschild singularity became BH Singularity Theorems Eddington-Finkelstein-Kruskal coordinates illuminated the darkest object, BH! They became astrophysical objects, stability? Vishu in 1970 established stability of Schwarzschild BH and pioneered the quasi normal mode analysis BH music Vishu Harmonic.
Black Hole Energetics Kerr Rotating BH Ergosphere Penrose Process -- Energy extraction -- powering high energy objects, Quasars, AGNs A particle coming from infinity may split into two in the ergosphere where one of the fragments may attain negative energy and falls into the hole and then the other comes out with energy > incident particle. That s how rotational energy of BH could be extracted and may power quasars.
Magenetic Penrose process PP s Astrophysical Viability: Relative velocity between fragments > c/2 astrophysically not viable. MPP(ND, Wagh, Dhurandhar) Rotating BH sits in magnetic field and the energy required to put a particle on negative energy state can now come from electromagnetic field making no demand on relative velocity.
Magenetic Penrose process Thus was MPP revived, Efficiency > 100%. It was all established in discrete particle accretion. Would it stand the test of realistic hydrodynamic accretion? MPP in high magnetic field limit is similar to Blandford Znajek process in which magnetic field threading the horizon gets wound up due to rotation and generates a quadrupole electric potential difference between poles and equator and energy flux is driven out as it discharges. In both cases, magnetic field plays as a catalytic agent to mine rotational energy .
MPP The current investigations bear out MPP s promise of efficiency exceeding 100% (this was first time predicted for MPP in 1985 (Ramesh s talk) has been borne out in the realistic hydrodynamic accretion a viable powering engine for quasars! It is a different matter that now MPP is being called as BZ process. They are different in the sense --- in zero magnetic field limit there is no extraction for BZ while MPP goes over to PP. May what that be, MPP as such was first considered by us in 1985.
Electromagnetics in curved spacetime Several authors have studied electromagnetic field in black hole spacetimes. RK Verma, Prasanna, Vishu, ..., An excellent review by AR Prasanna has just appeared summarizing an extensive body of work. There have also been attempts to couple Riemann tensor with two Maxwell tensors and then study its semi-classical consequences. Prasanna, S. Mohanty and others.
Compact Objects ... Pulsars: Rotating Neutron Stars Indirect Evidence of GW Milli Second Pulsars : Srinivasan & Radhakrishnan -- first models Several others: Panchu, Haridass, Vikram Soni, ...
Gravitational Lensing GR -- Hard Core Astrophysics Initial Work: JVN, Kumar Chitre, Kandu, D Narasimha, ... Indian contributions were at the pioneering stages
Gravitational waves Gravitational Wave: To Be or Not to Be? Bondi cleared the air with his information function In 1987-88: Dhurandhar goes to Schutz as a postdoc. BS Sathyaprakash, and several students follow. Leading group in GW Data Analysis comes up. Parallely Bala Iyer Damour, Blanchet, mastering the techniques of post-Lorentzian approximations and study of GW waveform .
GW Sathya is today one of the world leaders in GW community and over two dozen students trained at the hands of Sanjeev and Bala are Sprinkled all around in gravity wave groups. Ligo India is the due recognition of this small but highly influencial group globally.
GR and Beyond Palatini derivation for arbitrary connection. In 1925 Einstein assumed vanishing of torsion to get GR equation, and several authors have worked on this since then. J Pons and ND have shown that Einstein condition is really a gauge condition and hence we can obtain GR equation for arbitrary connection. It is the equation of motion for connection that demands it to be symmetric.
Gravity and Thermodynamics In 1992, Ted Jacobson brought out remarkable association between Einstein equation for spacetime admitting horizon and thermodynamical law. Reminiscent of Black hole area and entropy Laws of black hole physics. Paddy enormously extended this programme to Lovelock gravity and put it on solid footing. Makes a strong case for gravity being an emergent force.
Surface terms in action In derivation of GR equation by varying action, we ultimately convert variation of Ricci tensor which contains gravitational dynamics into a surface term a total derivative and throw it away. GR equation results from essentially variation of volume element. This is strange. Surface terms though classically irrelevant but are very relevant for quantum considerations. Most remarkably Paddy derives alternatively GR equation by manipulating surface term, and also connects the two through an interesting relation. This relation between bulk and surface is responsible for Holography. Gravity is universal and hence it cannot be shielded from any region. If separating boundary is null, it must have the imprint of what is blocked out.
Barbero Immirzi Parameter Surface terms: Euler, Pontryagin and Nieh Yan R Kaul, Shyam Date & S Sengupta showed N-Y is topological and its coupling is Barbero-Immirzi parameter. Kaul formulated gauge theory of gravity and supergravity. Gauge is a tricky business for gravity. Ashtekar Variables (1986), B-I parameter needed to cast the formalism with real variables. Samuel gave the Lagrangian formulation
Quantum Aspects JVN & Paddy: Quantizing conformal dgeree of freedom showed Big-Bang avoidance Special case of symmetry, LQC motivated by LQG which has a formal field theoretic backup also essentially does this. Recently LQC has been addressing anisotropy but not inhomogeneity as yet. A quantum Raychaudhury Equation Required ?
Quantum Aspects Kaul: Computed entropy of quantum BHs Kaul& Sengupta: Torsional instantons in quantum gravity TP Singh: Role of gravity in collapse of wave function Madhavan: Anamoly free quantum dynamics LQC: Shyam Date, Amit Ghosh, Golam Hossain, Parampreet Singh,...
Higher Dimensions and Lovelock High energy effects perhaps point to higher dimensions. What should be gravitational Equation in higher dimension? Is there any property that has yet remained unexplored which may point the direction? Einstein gravity is kinematic in 3D;i.e. Ricci =0 implies Riemann =0. Could this be universalized?
Pure Lovelock Recently ND has made a case for pure Lovelock for higher dimensions. Define Nth order Riemann and Ricci, then in all odd, D=2N+1, Ricci = 0 implies Riemann =0. It singles out pure Lovelock which has only one Nth order term, no summation. For pure Lovelock bound orbits exist in all even, D=2N+2, while for Einstein they exist only for D=4.
Braneworld Gravity Randall Sundrum braneworld: Curvature of bulk is used to make extra dimension small and then junction condition project bulk Weyl on the 3-brane. Black Hole on the brane is described by R-N charged BH metric (Roy Maartens, P Papadopoulous, V Rezania & ND) Sayan Kar and collaborators, and others have investigated various aspects of braneworld gravity.
Exact solutions S Majumdar (1947) Cylindrical Einstein- Maxwell solution: Papapetrou-Majumdar Radiating Kerr BH: Take Kerr metric transform to Eddington time, and then make mass function of the retarded time. But it doesn t satisfy the equation of null dust. But the solution has all desirable properties. Vaidya&Patel obtained two solutions
Exact Solutions Vaidya-Tikekar assumed t=const. Surface is spheriodal and instead of sphere and then built a model for star with satisfactory physical properties. S Mukherjee, et al obtained the general solution in this setting N Banerjee & S Sen: BD goes to GR limit only for traceful matter distribution, T non-zero. Few representatives names: A Banerjee, S Banerji, LK Patel, Tikekar, MC Durgapal, N Banerjee, BC Paul, ...
Prospects GR is now fully matured and well engrained theory for high energy physics, cosmology and astrophysics. GW: Will give rise to new view of the Universe, GW astronomy. Numerical Relativity $\Lambda$, Quantum spacetime/gravity Higher Dimensions, non-commutativity, ??? Singularity: Big-Bang, BH.
What made Difference ICGC series started in Dec. 1987 Summer Schools helped in grounding GR in Physics mid 80 s GR groups emerging in Institutes Regular IAGRG meetings and Many more FTAG began in 2001, growing strong
