Conditional Probability and Bayes Theorem
Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati
1 views • 5 slides
Floating Point Representation of Numbers
Floating point representation is crucial in computer arithmetic operations. It involves expressing real numbers as a mantissa and an exponent to preserve significant digits and increase the range of values stored. This normalized floating point mode allows for efficient storage and manipulation of r
0 views • 12 slides
Lipids: Waxes, Fats, and Fixed Oils
Lipids are organic compounds like waxes, fats, and fixed oils found in plants and animals. Fixed oils are reserve food materials, while fats are solid at higher temperatures. These substances are esters of glycerol and fatty acids, with various components giving them unique properties and flavors. C
1 views • 20 slides
Fixed Asset Management Procedures and Contacts Overview
This document provides an overview of fixed asset management procedures, contacts, categories, and responsibilities within the State of Connecticut. It covers the definition of fixed assets, capital vs. controllable equipment, receiving new assets, inventory audits, asset management responsibilities
1 views • 15 slides
The Coase Theorem: Property Rights and Economic Efficiency
The Coase Theorem, developed by economist Ronald Coase, posits that under certain conditions, bargaining related to property rights will lead to an optimal outcome regardless of the initial distribution. It provides a framework for resolving conflicts by emphasizing negotiation and efficient market
0 views • 10 slides
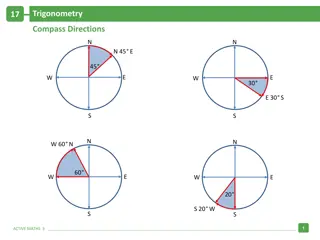
Trigonometry and Compass Directions Problem Solving
In this trigonometry problem, a ship travels from point A to point B and then to point C in specific directions. By applying the Pythagorean theorem, the distance from point C to A is calculated to be 7.2 km. The angle BCA is determined to be 34 degrees, and the direction of point C from A is found
0 views • 5 slides
The Pythagorean Theorem and Right-Angled Triangles
Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th
3 views • 25 slides
Introduction to Lipid Biosynthesis and Fixed Oils in Pharmacognosy Lecture
In this lecture by Asst. Prof. Dr. Ibrahim Salih, the focus is on lipid biosynthesis, specifically the three phases involved: glycerol formation, fatty acid biosynthesis, and triglyceride production. The classification of fixed oils into drying, semi-drying, and non-drying categories based on their
0 views • 13 slides
Engineering Mechanics: Lami's Theorem and Cylinder Reactions Problem
This course material covers Lami's Theorem in Engineering Mechanics taught by Ranbir Mukhya. It includes an outline of the theorem, problem scenarios involving cylinders with given weights and diameters, and the determination of reactions at various points. Detailed force diagrams and calculations a
3 views • 8 slides
Insights into the Mean Value Theorem and Its Applications
Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista
1 views • 14 slides
The Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
2 views • 31 slides
Conformal Window in SU(3) Gauge Theories: IR Fixed Points and Scaling Hypothesis
Study of temporal propagator behaviors near fixed points, effective masses in free fermion examples, and strategies to find zero of beta functions in SU(3) gauge theories. Investigation of coupling constants and lattice sizes to determine existence of Banks-Zaks fixed point.
0 views • 11 slides
Superposition Theorem in Electrical Circuits
Superposition theorem in electrical circuits states that the effects of multiple voltage and current sources in a network can be analyzed independently and then combined algebraically. This allows for calculating the voltage and current distribution in a network more efficiently. The theorem involve
0 views • 9 slides
Lami's Theorem in Physics
Lami's Theorem is an equation that explains how the magnitudes of forces acting on a point keep an object in equilibrium. This theorem relates the forces with corresponding angles and is derived by understanding the sum of forces acting on a point. By utilizing complementary angles and the sine rule
0 views • 8 slides
Floating Point Representation in Binary Systems
In computer systems, decimal numbers are represented in memory using scientific notation. This involves moving the decimal point and using mantissa and exponent to maintain precision and range. The transition to representing numbers in binary involves multiplying by 2 to the power instead of 10. Uti
2 views • 22 slides
Exploring the Pythagorean Theorem and Its Origins
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines
0 views • 21 slides
Rolle's Mean Value Theorem in Calculus
Rolle's Mean Value Theorem states that if a function is continuous in a closed interval, differentiable in the open interval, and the function values at the endpoints of the interval are equal, then there exists at least one point where the derivative of the function is zero. This theorem is verifie
1 views • 11 slides
Bayes Theorem in NLP: Examples and Applications
Introduction to Bayes Theorem in Natural Language Processing (NLP) with detailed examples and applications. Explains how Bayes Theorem is used to calculate probabilities in diagnostic tests and to analyze various scenarios such as disease prediction and feature identification. Covers the concept of
0 views • 13 slides
Ladner's Theorem in Computational Complexity Theory
Ladner's Theorem is a significant result in computational complexity theory that deals with NP-intermediate problems, which are languages in NP neither in P nor NP-complete. The theorem states that if P is not equal to NP, then there must exist an NP-intermediate language. The proof involves a delic
1 views • 48 slides
Problem Solving with Pythagoras Theorem in Geometry
Explore the application of Pythagoras Theorem in solving problems related to right-angled triangles, diagonals of shapes like rectangles and rhombuses, and the height of triangles. Learn how to use Pythagoras Theorem effectively by drawing diagrams, identifying known lengths, and using the theorem t
0 views • 8 slides
Brouwer's Fixed Point Theorem and Nash's Proof in Algorithmic Game Theory
Explore the foundational theorems of Brouwer and Nash in Algorithmic Game Theory. Dive into Brouwer's Fixed Point Theorem, showcasing the existence of fixed points in continuous functions. Delve into Nash's Proof, unveiling the Nash equilibrium in game theory. Discover visualizations and constructio
1 views • 23 slides
Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Fixed Income Securities: Bonds Overview
Learn about fixed income securities in week 2 of the Fundamentals of Investment course, focusing on bond characteristics, types, and risks. Bonds are vital debt instruments issued by organizations to raise funds, with features like fixed maturity dates and interest rates. Explore various bond types
1 views • 20 slides
Rolle's Theorem and The Mean Value Theorem in Calculus
Rolle's Theorem states that for a continuous and differentiable function on a closed interval with equal function values at the endpoints, there exists at least one point where the derivative is zero. The Mean Value Theorem asserts that for a continuous and differentiable function on an interval, th
0 views • 5 slides
Introduction to Analysis: Mean Value Theorem and Related Theorems
This resource delves into key concepts such as the Mean Value Theorem, Fermat's Theorem, Rolle's Theorem, Extreme Value Theorem, local maximums, and more. It presents important results and explores proofs in the context of analysis.
1 views • 71 slides
Freezing Point Depression and Molality for Solutions
Introduction to molality and freezing point depression in solutions. Molality is a way to measure solution concentration, calculated using moles of solute and kilograms of solvent. By calculating the moles of NaCl in a salt solution and the mass of the solvent (ice/water), the molality can be determ
2 views • 9 slides
Introduction to Applying Pythagorean Theorem in Right Triangles
In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,
1 views • 13 slides
Fixed-Income Securities for Investment
Fixed-income securities offer fixed returns up to a redemption date or indefinitely, comprising long-term debt securities and preferred stocks. These investments involve various risk factors, including default risk. Long-term debt securities, such as bonds, provide a safe asset but require careful c
2 views • 47 slides
Binomial Theorem: Expansion, Examples, and Applications
Binomial theorem is a powerful mathematical concept used to expand expressions involving binomials. This presentation explores the basics of binomial expansion, formulae for positive, negative, and fractional indices, along with examples demonstrating its application. By leveraging the binomial theo
1 views • 10 slides
Automated Theorem Proving in Lean
Dive into the world of automated theorem proving in Lean with a focus on formal verification, history, and the use of logic and computational methods. Explore how programs can assist in finding and verifying proofs, as well as the significance of interactive theorem provers. Discover the evolution o
1 views • 35 slides
Point-to-Point Protocol (PPP) and Serial Communications in WANs
This content explores the Point-to-Point Protocol (PPP), outlining its components, establishment of sessions, authentication protocols, and configuration. It also delves into WAN connection options, serial and parallel ports communication, and serial communication standards for LAN-to-WAN connection
0 views • 31 slides
Triangles Inequalities and The Hinge Theorem
Understanding the inequalities in triangles using the Hinge Theorem. The theorem explains how the length of the third side of a triangle relates to the included angles and congruent sides in different triangle configurations. Explore problems that involve applying the Hinge Theorem and its converse
0 views • 8 slides
Pythagoras’ Theorem
The Pythagoras Theorem explains the relationship between the sides of a right-angled triangle. Discover the history, visualization, and application of this fundamental mathematical concept through a detailed exploration. Uncover how to use Pythagoras Theorem to calculate the length of the hypotenuse
0 views • 14 slides
Fixed-Point Iteration in Mathematics: Understanding the Derivative Mean-Value Theorem
Concept of fixed-point iteration in mathematics through examples and explanations, including the derivative mean-value theorem. Learn how to locate roots using iterative methods and understand the importance of fixed points in mathematical functions.
0 views • 8 slides
Bisectors
Explore the concepts of perpendicular and angle bisectors through the Perpendicular Bisector Theorem, Converse of the Perpendicular Bisector Theorem, Angle Bisector Theorem, and Converse of the Angle Bisector Theorem. Learn how these theorems are applied in geometry with illustrative examples. Get i
1 views • 7 slides
Fixed Assets Management
Fixed assets are tangible properties owned or controlled by a business that depreciate over time. Managing fixed assets involves processes like purchasing, categorizing, and accounting for these assets. This involves creating purchase orders, referencing invoices, and adding items to the fixed asset
0 views • 17 slides
FIXED ASSETS
Fixed assets are essential tangible properties owned by an organization for long-term use. This includes equipment such as office furniture, computers, vehicles, and more. Proper management of fixed assets involves tracking, tagging, and ensuring accurate financial reporting. In a university setting
0 views • 9 slides
Optimizing Fixed Income Allocation in the Current Environment
Explore insights on optimizing your fixed income allocation in the current environment, including performance of government and corporate bonds during equity drawdowns, 10-year bond yields, corporate bond OAS data, portfolio construction correlations across markets, and enhancing fixed income effici
0 views • 10 slides
Understanding Stability of Fixed Points in Classical Mechanics and Electromagnetism
Explore the concept of fixed points in phase-space, their stability, and linearization for stability analysis in classical mechanics and electromagnetism. Learn how to identify stable and unstable fixed points using vector diagrams and eigenvalues. Gain insights into the motion near fixed points and
0 views • 14 slides
Fixed vs Flexible Exchange Rates: Advantages and Disadvantages
Learn about the differences between fixed and flexible exchange rates, including the advantages and disadvantages of each. Explore how fixed rates can offer stability and encourage investment while potentially causing conflicts with other macroeconomic objectives. On the other hand, flexible rates a
0 views • 9 slides