Bisectors
5.1 Perpendicular and Angle
Bisectors
Guiding Question:
Vocabulary/Theorems
•
Equidistant:
when a point is the same
distance from two or more objects
•
5-1-1: Perpendicular Bisector Theorem
:
If a point is on the perpendicular bisector
of a segment, then it is equidistant from
the endpoints of the segment.
–
XA=XB
A
B
X
Y
•
5-1-2 Converse of the Perpendicular Bisector
Theorem: If a point is equidistant from the
endpoints of a segment, then it is on the
perpendicular bisector of a segment.
XY AB
YA ~ YB
A
B
X
Y
•
5-1-3 Angle Bisector Theorem: if a point is
on the bisector of an angle, then it is
equidistant from the sides of the angle
•
5-1-4 Converse of the Angle Bisector
Theorem: If a point in the interior of an
angle is equidistant from the sides of the
angle, then it is on the bisector of the
angle.
A
P
B
C
˂APC ˂BPC
AC=BC
•
Example 1:
•
Example 2:
Find the measure
of MN
Find the
measure of BC
M
N
L
P
2.6
B
C
D
A
12
38
38
Perpendicular Bisector
Angle Bisector
•
Example 3
•
Example 4
B
A
D
C
G
F
E
H
Find the measure of BC
Find the m<EFH, given that
m<EFG=50
7.2
•
Homework DUE WEDNESDAY!
–
Page 304: 2-8 even, 12-16 even
Explore the concepts of perpendicular and angle bisectors through the Perpendicular Bisector Theorem, Converse of the Perpendicular Bisector Theorem, Angle Bisector Theorem, and Converse of the Angle Bisector Theorem. Learn how these theorems are applied in geometry with illustrative examples. Get insights into finding measurements of segments and angles using bisectors. Homework assignments included for practice.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
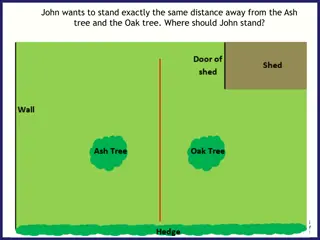
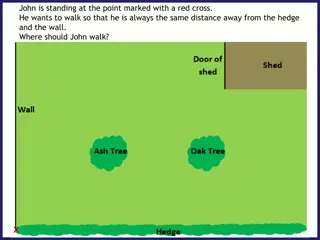
5.1 Perpendicular and Angle Bisectors Guiding Question:
Vocabulary/Theorems Equidistant: when a point is the same distance from two or more objects 5-1-1: Perpendicular Bisector Theorem: If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. XA=XB X A B Y
5-1-2 Converse of the Perpendicular Bisector Theorem: If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of a segment. XY AB YA ~ YB X A B Y
5-1-3 Angle Bisector Theorem: if a point is on the bisector of an angle, then it is equidistant from the sides of the angle A AC=BC C B P 5-1-4 Converse of the Angle Bisector Theorem: If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle. APC BPC
Perpendicular Bisector N Find the measure of MN Example 1: 2.6 M L P Example 2: Find the measure of BC B 38 A D 12 38 C
Angle Bisector Example 3 B Find the measure of BC C 7.2 D A Example 4 G Find the m<EFH, given that m<EFG=50 H E F
Homework DUE WEDNESDAY! Page 304: 2-8 even, 12-16 even
