Understanding Tangents and Circles in Geometry
Explore the relationships among inscribed angles, radii, and chords in circles to understand the properties of tangents and their intersections with circles. Learn about the theorems related to tangent lines, segments, and exterior points, and discover the properties of arcs and central angles within circles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Chapter 12.1 Common Core G.C.2 Identify and describe relationships among inscribed angels, radii, and chords the radius of a circle is perpendicular to the tangent where the radius intersects the circle. Objective To use properties of a tangent to a circle.
Chapter 12.1 Notes Circles is the set of all pts in a plane that are equidistant from a given pt, called the center
Internally and Externally Tangents The Circles are internally and externally tangent. The Lines are internally and externally tangent.
Thm If a line is tangent to a circle, it is to the radius drawn to the point of tangency If then Thm In a plane, if a line is to a radius of a circle at its endpts. on the circle, then the line is tangent to the circle. If then
Thm If 2 segments from the same exterior pt are tangent to a circle, then they are . If then
Chapter 12.2 Notes Common Core G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Objectives To use congruent chords, arcs, and central angles. To use perpendicular bisectors to chords.
Chapter 12.2 Notes Central Angle an angle made with the center of the circle. Minor Arc is a central angle less than 180 Semicircle is a central angle that is exactly 180 Major Arc is a central angle more than 180
Arc Addition Postulate m ABC = m AB + m BC Thm AB BC AB BC Thm DE EF, DG GF
Thm JK is a diameter of the circle Thm AB CD EF EG
Chapter 12.3 Notes Common Core G.C.2, G.C.3, G.C.4 Identify and describe relationships among inscribed angles, radii, and chords. Prove properties of angles for a quadrilateral inscribed in a circle. Objectives To find the measure of an inscribed angle. To find the measure of an angle formed by a tangent and a chord.
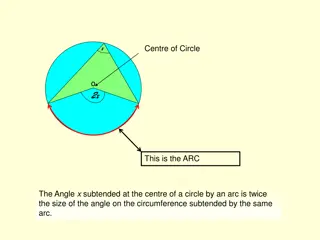
Chapter 12.3 Notes Inscribed Angles is an angle whose vertex is on a circle and whose sides contain chords of the circle. Inscribed angle is half the measure of the intercepted arc.
Thm If 2 inscribed angles of a circle intercept the same arc, then the angles are congruent. Thm If a rt hypotenuse is a diameter of the circle and vise versa. is inscribed in a circle, then the
Thm A Quadrilateral can be inscribed in a circle if and only if its opposite angles are supplementary The Quad. is inscribed in the circle and the circle is circumscribed about the Quad.
Thm If a tangent and an chord intersect at a pt. on a circle, then the measure of each angle formed is the measure of its intercepted arc.
Chapter 12.4 Common Core G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Objectives To find measures of angles formed by chords, secants, and tangents. To find the lengths of segments associated with circles.
Chapter 12.4 Thm If 2 chords intersect in the interior of a circle, then the measure of each angle is the sum of the measures of the arcs intercepted by the angle and its vertical angles.
Thm If a tangent and a secant, 2 tangents, or 2 secants intersect in the exterior of a circle, then the measure of the angle formed is the difference of the measures of the intercepted arcs.
Thm If 2 chords intersect in the interior of a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord. Thm If 2 secant segments share the same endpt outside a circle, then the product of the length of one secant segment and the length of its external segment equals the product of the length of the other secant segment and the length of its external segment
Thm If a secant segment and a tangent segment share an endpt. Outside a circle, then the product of the length of the secant segment and the length of its external segment equals the square of the length of the tangent segment.
Chapter 12.5 Notes Common Core G.GPE.1 Derive the equation of a circle given center and radius using the Pythagorean Theorem. Objectives To write the equation of a circle. To find the center and radius of a circle.
Chapter 12.5 Notes Standard equation of a circle (x h)2+ (y k)2= r2 Center (h,k) Radius is r
Chapter 12.6 Notes Common Core G.GMD.4 Identify three- dimensional objects generated by rotations of two-dimensional objects. Objectives To draw and describe a locus.
Chapter 12.6 Notes Locus is the set of all points in a plane that satisfy a given condition or a set of given conditions. Finding a Locus 1) Draw any figures that are given in the statement of the problem. 2) Locate several pts. that satisfy the given condition 3) Continue drawing pts. Until you can recognize the pattern. 4) Draw the locus and describe it in words.