Understanding Isosceles Triangles in Circles
Exploring the properties and characteristics of isosceles triangles within circles, focusing on identifying, understanding angles, and special properties within these geometric shapes. Key concepts covered include equal lengths, equal angles, and angle calculations within isosceles triangles forming in circles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
The Circle Isosceles Triangles in Circles Right angle in a Semi-Circle Tangent Line to a Circle Diameter Symmetry in a Circle Circumference of a Circle Length of an ARC of a Circle Area of a Circle Area of a SECTOR of a Circle Summary of Circle Chapter 2
Isosceles triangles in Circles Aim of Today s Lesson To identify isosceles triangles within a circle. 3
Isosceles triangles in Circles When two radii are drawn to the ends of a chord, An isosceles triangle is formed. A B xo xo C 4
Isosceles triangles in Circles Special Properties of Isosceles Triangles Two equal lengths Two equal angles Angles in any triangle sum to 180o 5
Isosceles triangles in Circles o. Q. Find the angle x Solution Angle at C is equal to: B 360 280 80 o o o = o C x Since the triangle is isosceles we have 2 x + A 280o o o o = 80 180 o o x = 2 100 o o x = 50 6
Isosceles triangles in Circles 7
Semi-circle angle Aim of Today s Lesson To find the angle in a semi-circle made by a triangle with hypotenuse equal to the diameter and the two smaller lengths meeting at the circumference. 8
Semi-circle angle Tool-kit required 1. Protractor 2. Pencil 3. Ruler 9
Semi-circle angle 1. Using your pencil trace round the protractor so that you have semi-circle. 2. Mark the centre of the semi-circle. You should have something like this. 10
Semi-circle angle x x x x Mark three points x 1. Outside the circle 2. On the circumference 3. Inside the circle x x x x 11
Semi-circle angle x For each of the points x Form a triangle by drawing a line from each end of the diameter to the point. Measure the angle at the various points. Log your results in a table. Circumference Outside x Inside 12
Semi-circle angle x x x Outside < 90 Inside > 90 Circumference = 90 o o o 13
Tangent line Aim of Today s Lesson To understand what a tangent line is and its special property with the radius at the point of contact. 14
Tangent line A tangent line is a line that touches a circle at only one point. Which of the lines are tangent to the circle? 15
Tangent line The radius of the circle that touches the tangent line is called the point of contact radius. Special Property The point of contact radius is always perpendicular (right-angled) to the tangent line. 16
Tangent line Q. Solution Right-angled at A since AC is the radius at the point of contact with the Tangent. By Pythagoras Theorem we have + a b + 8 a a a Find the length of the tangent line between A and B. B 10 C A 8 c 10 10 100 36 2 2 2 = = = = 2 2 2 8 2 2 2 64 6 36 2 = a = = 17
Tangent line 18
Diameter symmetry Aim of Today s Lesson To understand some special properties when a diameter bisects a chord. 19
Diameter symmetry C 1. A line drawn through the centre of a circle through the midpoint a chord will ALWAYS cut the chord at right-angles 2. A line drawn through the centre of a circle at right-angles to a chord will ALWAYS bisect that chord. O A B 3. A line bisecting a chord at right angles will ALWAYS pass through the centre of a circle. D 20
Diameter symmetry Q. Find the length of the chord A and B. Solution B Radius of the circle is 4 + 6 = 10. Since yellow line bisect AB and passes through centre O, triangle is right-angle. 10 O By Pythagoras Theorem we have + = a b c + = 6 10 a 4 6 2 2 2 Since AB is bisected The length of AB is 2 2 2 A a a 10 100 36 64 6 2 2 2 = = = 64 2 = length 2 8 16 = = a 8 = AB 21
Circumference of a circle Aim of Today s Lesson To be able to use the formula for calculating the circumference of a circle 23
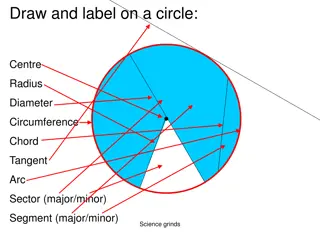
Circumference of a circle Main parts of the circle radius O Diameter 2 D = r Circumference = C D 24
Circumference of a circle Q. Find the circumference of the circle ? Solution = = = 4cm C C C D 8 25.12 cm 25
Circumference of a circle Q. The circumference of the circle is 60cm ? Find the length of the diameter and radius. Solution = = 60 =60 D C D D 2 r = D 19 2r 19 2 9.5 = cm r = = r cm D 19 cm 26
Circumference of a circle 27
length of the arc of a circle Aim of Today s Lesson To find and be able to use the formula for calculating the length of an arc. 28
Arc length of a circle Q. What is an arc ? Answer A An arc is a fraction of the circumference. minor arc B major arc 29
Arc length of a circle Find the circumference of the circle ? Q. Solution = = = 10cm C C C D 20 62.8 cm 30
Arc length of a circle Q. Find the length of the minor arc XY below ? x connection Arc length D Arc angle 360o = y 6 cm o 45 45 360 o arc length ( 12) = o o 360 arc length 4.71 cm = 31
Arc length of a circle Q. Find the length of the minor arc AB below ? Arc length D Arc angle 360o = connection A 9 cm 60 360 o o 60 arc length ( 18) = o B arc length 9.42 cm = 32
Arc length of a circle Q. Find the length of the major arc PQ below ? Arc length D Arc angle 360o = connection P 10 m 260 360 o o o 260 100 arc length ( 20) = o Q arc length 45.38 cm = 33
length of the arc of a circle 34
The Area of a circle Aim of Today s Lesson To come up with and be able to use the formula for calculating the area of a circle 35
The Area of a circle If we break the circle into equal sectors And lay them out side by side We get very close to a rectangle. 1 8 2 7 3 6 5 8 6 4 4 2 3 7 1 5 36
The Area of a circle If we cut the sectors Thinner and thinner then we get closer and closer to a rectangle. Hence we can represent the area of a circle by a rectangle. 8 6 4 23 7 1 5 thinner and thinner sectors r r 37
The Area of a circle r r Area of a rectangle Area of a rectangle l b = r r r 2 = = But the area inside this rectangle is also the area of the circle Area of a circle r 2 = 38
The Area of a circle Q. Find the area of the circle ? Solution A = = A A = 4cm r 2 50.26 4 2 cm 2 39
The Area of a circle Q. The diameter of the circle is 60cm. Find area of the circle? Solution A = D = r 2 60 2 2827.43 r 30 cm = = 2 A 30 2 = A cm 2 = 41
The Area of a circle 2. Q. The area of a circle is 12.64 cm Find its radius? Solution A = = r 2 12.64 r 2 12.64 r 4 cm 2 = = 4 r 2 cm = = 43
Sector area of a circle Aim of Today s Lesson To find and be able to use the formula for calculating the sector of an circle. 44
Area of Sector in a circle A minor sector B major sector 45
Area of Sector in a circle Find the area of the circle ? Q. Solution A = = A A = 10cm r 2 314 10 cm 2 2 46
Area of Sector in a circle Find the area of the minor sector XY below ? x connection Area Sector r2 Sector angle 360o = y 6 cm o 45 45 360 o Area of Sector ( 6 ) 2 = o o 360 Area Sector 14.14 cm 2 = 47
Area of Sector in a circle Q. Find the area of the minor sector AB below ? connection Area Sector r2 Sector angle 360o A = 9 cm 60 360 o o 60 Area Sector ( 9 ) 2 = o B Area Sector 42.41 cm 2 = 48
Area of Sector in a circle Q. Find the area of the major sector PQ below ? connection Sector Area r2 Sector angle 360o = P 10 m 260 360 o o o 260 100 Sector Area ( 10 ) 2 = o Q Area Sector 226.89 cm 2 = 49