Illustrated Methods of Multiplication and Division
Remember, any multiplication can be
reversed in 2 ways, using division:
Long multiplication
Long division
Ways to multiply (1) – lattice method
If you only know the
lattice method, long
division will not
make sense
Ways to multiply (2a) – long multiplication
Ways to multiply (2b) – long multiplication
Can we reverse the process?
Division
“We need an easy way of splitting it into single digit multiples of 457”
Short division (simple example, part1)
Swop the numbers and write a division sign:
How many 3’s go into 7? “2, remainder 1”
2 is in the
thousands
column.
We have “made” 2000×3=6000 so far.
Now, how many 3’s go into the
remaining 1854?
Short division (simple example, part 2)
How many 3’s go into 5? “1, remainder 2”
26 means 2600.
We have “made” 2600×3=7800 so far.
Now, how many 3’s go into the
remaining 54?
How many 3’s go into 18? “6, remainder 0”
261 means 2610.
We have “made” 2610×3=7830 so far.
Now, how many 3’s go into the
remaining 24?
Short division (simple example, part 3)
How many 3’s go into 24? “8, remainder 0”
You can use short division
with a longer divisor
(e.g. 457) but
long division
is
easier
.
We do the same thing,
but write out each
subtraction to make it
clearer
Long division (1 digit example)
2000×3=6000 (less than 7854, OK)
but 3000×3=9000 would be
too big
This is just to show
how
long division works
.
You do not
need
long
division for such an easy
question.
We repeat the process
until there is
no
remainder left!
Long division (1 digit example)
600×3=1800 (less than 1854, OK)
but 700×3=2100 would be
too big
Carry on…
Long division (1 digit example)
10×3=30 (less than 54, OK)
but 20×3=60 would be
too big
Carry on…
Long division (1 digit example)
8×3=24 as required.
Remainder 0 so we have finished.
Long division with a long divisor (a)
It’s just like long multiplication, but subtracting instead of adding!
Dividing:
Multiplying:
Long division with a long divisor (b)
Long division of decimals
We can make the division easier by multiplying each side by a power of 10
until we have at least one integer
EQUIVALENT
FRACTIONS.
Remember the
“decimal places” rule.
The content explains various methods of multiplication and division, including long multiplication, lattice method, and short division, with detailed examples and visual aids. It covers concepts like reversing multiplication through division, using single-digit multiples, and step-by-step division techniques. The illustrations make it easier to understand and apply these mathematical operations effectively.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
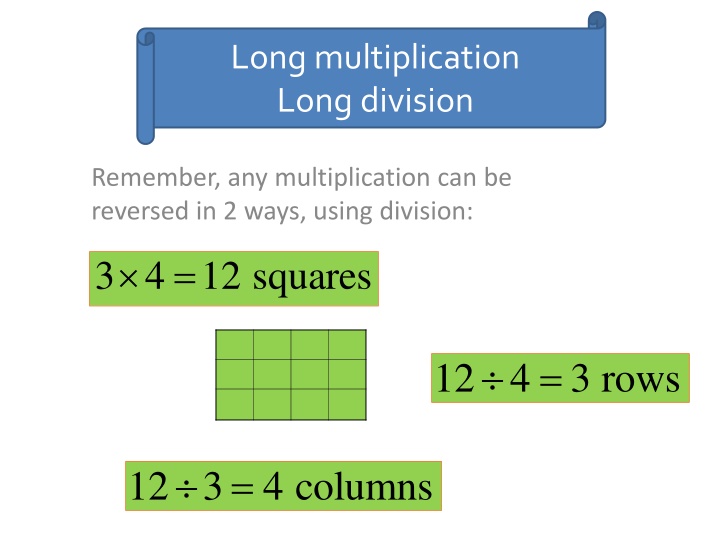
Long multiplication Long division Remember, any multiplication can be reversed in 2 ways, using division: 3 4 12 squares = 12 4 = 3 rows 12 3 = 4 columns
Ways to multiply (1) lattice method 2.34 3.29 = 7.6986 If you only know the lattice method, long division will not make sense
Ways to multiply (2a) long multiplication ( 457 111 457 1 10 100 = + ) + = 50727 457 111 457 4570 45700 + 50727 1 457 10 457 100 457
Ways to multiply (2b) long multiplication ( 457 111 457 100 10 1 = ) + + = 50727 457 111 45700 4570 457 50727 100 457 10 457 1 457 Can we reverse the process?
Division How to do 50727 457 ? We need an easy way of splitting it into single digit multiples of 457 ( ) = 45700 4570 457 + = + = 100 10 1 + + 50727 457 111 457 = Hence 50727 457 111 We will see how in a moment first, let s start with something simpler.
Short division (simple example, part1) Find 7854 3 Swop the numbers and write a division sign: 3 7 854 How many 3 s go into 7? 2, remainder 1 2 3 7 854 2 is in the thousands column. We have made 2000 3=6000 so far. Now, how many 3 s go into the remaining 1854? 1
Short division (simple example, part 2) How many 3 s go into 18? 6, remainder 0 2 6 3 7 854 26 means 2600. We have made 2600 3=7800 so far. Now, how many 3 s go into the remaining 54? 1 How many 3 s go into 5? 1, remainder 2 2 61 3 7 85 4 261 means 2610. We have made 2610 3=7830 so far. Now, how many 3 s go into the remaining 24? 1 2
Short division (simple example, part 3) How many 3 s go into 24? 8, remainder 0 2 61 8 3 7 85 4 = 7854 3 2618 1 2 You can use short division with a longer divisor (e.g. 457) but long division is easier. We do the same thing, but write out each subtraction to make it clearer
Long division (1 digit example) 2 3 7854 6000 - 1854 2000 3=6000 (less than 7854, OK) but 3000 3=9000 would be too big This is just to show how long division works. You do not need long division for such an easy question. We repeat the process until there is no remainder left!
Long division (1 digit example) 26 3 7854 6000 - 1854 1800 - 54 600 3=1800 (less than 1854, OK) but 700 3=2100 would be too big Carry on
Long division (1 digit example) 261 3 7854 6000 - 1854 1800 - 54 30 - 24 10 3=30 (less than 54, OK) but 20 3=60 would be too big Carry on
Long division (1 digit example) 2618 3 7854 6000 - 1854 1800 - 54 30 - 24 24 - 0 = 7854 3 2618 2000 3 each pair is the remainder at this stage and our attempt to match it 600 3 10 3 8 3=24 as required. 8 3 Remainder 0 so we have finished.
Long division with a long divisor (a) How to do 50727 457 ? 111 457 50727 45700 - 5027 4570 - 457 457 - 0 100 457 10 457 1 457
Its just like long multiplication, but subtracting instead of adding! Dividing: Multiplying: 111 457 111 45700 4570 457 50727 457 50727 45700 - 5027 4570 - 457 457 - 0 100 457 10 457 1 457
Long division with a long divisor (b) How to do 7347 31 ? 237 31 7347 6200 - 1147 930 - 217 217 - 0 200 31 1 31=31 2 31=62 3 31=93 4 31=124 5 31=155 6 31=186 7 31=217 8 31=248 9 31=279 30 31 7 31
Long division of decimals We can make the division easier by multiplying each side by a power of 10 until we have at least one integer = 0.08056 0.053 80.56 53 EQUIVALENT FRACTIONS. 1.52 53 80.56 53 - 27.56 26.5 - 1.06 1.06 - 0 1 53=53 2 53=106 3 53=159 4 53=212 5 53=265 6 53=318 7 53=385 8 53=424 9 53=477 1 53 0.5 53 0.02 53 Remember the decimal places rule.
