Polynomial Long Division Review and Practice
Polynomial Long Division Review
A)
B)
SYNTHETIC DIVISION:
STEP #1
:Be sure the polynomial is in stardanrd form with
no gaps
STEP #2
:
Solve the Binomial Divisor = Zero (this is just the
opposite of the constant in the divisor)
STEP #3
:
Write the ZERO-value, then all the
COEFFICIENTS of Polynomial.
2
5
-13
10
-8
STEP #4
:
Last Answer is your REMAINDER
Write the coefficient “answers” in descending order starting
with a Degree ONE LESS THAN Original Degree and include
NONZERO REMAINDER OVER DIVISOR at end
2
5
-13
10
-8
5
10
-3
-6
4
8
0 = Remainder
5
-3
4
SAME ANSWER AS LONG DIVISION!!!!
SYNTHETIC DIVISION:
Practice
[1]
[2]
This content provides a detailed review on polynomial long division including step-by-step instructions, examples, and synthetic division practice problems. It covers topics such as descending polynomial order, solving binomial divisors, writing coefficients, determining remainders, and obtaining final answers. The included images further illustrate the processes involved in polynomial long division and synthetic division.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
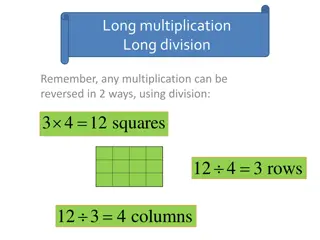
Polynomial Long Division Review + + 3 2 1 A) y y y ( 6 )( ) 2 + + 3 2 x x x x 5 ( 13 10 ) 8 ( ) 2 B) 18 + y 0 2 + 3 6 y y x + 5 3 4 2 x 2 + + + + 3 2 y y y y 2 6 + + 3 2 x x x x 2 5 13 10 8
SYNTHETIC DIVISION: STEP #1:Be sure the polynomial is in stardanrd form with no gaps Descending Polynomial + + 3 2 x x x x 5 ( 13 10 ) 8 ( ) 2 + + 3 2 Order x x x : 5 13 10 8 STEP #2: Solve the Binomial Divisor = Zero (this is just the opposite of the constant in the divisor) ; 0 2 = = x = = x 2 STEP #3: Write the ZERO-value, then all the COEFFICIENTS of Polynomial. 2 5 -13 10 -8
5 -13 10 -8 10 2 -6 8 5 -3 0 = Remainder 4 STEP #4: Last Answer is your REMAINDER Write the coefficient answers in descending order starting with a Degree ONE LESS THAN Original Degree and include NONZERO REMAINDER OVER DIVISOR at end 5 x x + + 2 3 4 5 -3 4 + + = = 3 2 x x x x 5 ( 13 10 ) 8 ( ) 2 x + + 2 x 5 3 4 SAME ANSWER AS LONG DIVISION!!!!
SYNTHETIC DIVISION: Practice ( ) 12 5 2 + + + + x x x x [1] + + 3 2 ( ) 4 [2] + + + + 4 3 2 x x x x ( 5 13 10 ) ( ) 1
