Understanding Add Factors and Forecasting in Regression Analysis
Regression analysis involves estimating parameters and fitting lines to data, with errors represented by residuals. Errors in forecasting can be caused by structural breaks or one-off events like droughts, leading to growth shifts. Add factors represent the difference between a statistical forecast and the actual forecast, accounting for unobserved variables and judgment calls. Mixing judgment with model information can affect the forecasting accuracy.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
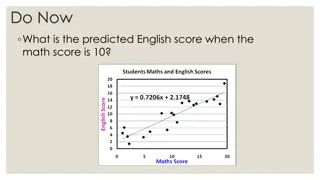
Regressions: The background of add-factors The output of a regression includes Estimated parameters A fitted line Residual The difference between the actual value and the fitted line
Errors: A simple example The regression looks something like: ??= ? + ???+ ?? We know from introductory statistics that the (fitted value) is simply ??= ? + ??? ??= ?? ?? ??~?(0,?2)
Forecast inference from errors A well-specified model means that ??=iid with ? ?? = 0 Occasionally this story does not pan out Structural break Can cause growth shift in ?? One-off events such as droughts If not captured in the intercept could cause level shift in ??, but still constant
In-sample Errors ?? ?? ?? ? = ? ? = ? ? = 0
Add Factors and Forecasting The add factor is analogous to the error term In history, unobserved variables or random events cause ?t to differ from the regressions fitted value ?? During the forecast period the actual number we forecast may differ from the fitted value of our equation because of outside of the model information (judgement) We call this difference the add factor the amount by which our forecast differs from the purely statistical conditional forecast built into the model
Add Factors, Judgement and Forecasting The add factor is defined as the difference between the conditional forecast from the model (conditional on the state of all other variables) and the actual forecast ??t ?? ?? The add factor measures the extent to which outside of the model information (Judgement) has caused our forecast to deviate from the purely statistical one
Mixing Judgement and Model Information ?? ?? ?? ? = ? ? = ? ? = 0
Add-factors, Judgement and Forecasting During the last observation there is a large error (difference between fitted value and actual) Depending on our judgement about the nature of that error we can use the add factor to generate different forecasts. Assume four alternative judgements 1. 2. The error is a one-off random error The error reflects a permanent unmodelled shift in the level of the dependent variable (say a factory closed) The error represents a permanent shift in the growth rate of the dependent variable (say new technology has rendered further investment in the sector unprofitable) Temporary deviation that slowly returns to normal (recovery from flood) 3. 4.
Add-factors, Judgement and Forecasting One off event ??+? 1. Assume that error at t=k was one-off, Set addfactor for t> k = 0. Forecast equals Fitted Value ?? ?? ? = ? ? = ? ? = 0
Add-factors, Judgement and Forecasting Permanent shift in level of activity ??+? ?? 2. Assume that error is a permanent shift (plant closed), set addfactor for t> k = the error in period k. (shift in constant) ?? ? = ? ? = ? ? = 0
Add-factors, Judgement and Forecasting Permanent slower growth ??+? ?? 3. Assume a permanent shift in growth rate (no new investment), set addfactor gets increasingly negative. (shift in beta) ?? ? = ? ? = ? ? = 0
Add-factors, Judgement and Forecasting Temporary negative effect ??+? 4. Assume a temporary shift that gradually fades away to zero (flood from which economy gradually recovers), addfactor slowly returns to zero. ?? ?? ? = ? ? = ? ? = 0
Add-factors, Judgement and Forecasting ??+? 1. Assume that error at t=k was one-off, Set addfactor for t> k = 0. Forecast equals Fitted Value ?? 2. Assume that error is a permanent shift (plant closed), set add factor for t> k = the error in period k. (shift in constant) ?? 3. Assume a permanent shift in growth rate (no new investment), set add factor gets increasingly negative. (shift in beta) 4. Assume a temporary shift that gradually fades away to zero (flood from which economy gradually recovers), addfactor slowly returns to zero. ? = ? ? = ? ? = 0
Add-factors and Forecasting: Judgement Size Front-end provides easy access to size of add-factor in growth and level terms Note: MS+AF=USER In 2018 user judgment added 0.3% pts to growth 2.3%=2%+0.3%