Triangle Congruence Properties
Starter
What’s the same? What’s different?
42°
42°
42°
32°
6cm
6cm
6cm
9cm
4cm
4cm
4cm
8cm
Definitions
Congruent shapes
have all sides and angles equal.
Similar shapes
have all angles equal but one is an
enlargement of the other.
Are these triangles congruent?
For triangles to be congruent, three
properties must be the same:
SSS
Congruence
4cm
4cm
6cm
6cm
3.5cm
3.5cm
Are these triangles congruent?
For triangles to be congruent, three
properties must be the same:
SAS
Congruence
4cm
4cm
3.5cm
3.5cm
78°
78°
Are these triangles congruent?
For triangles to be congruent, three
properties must be the same:
ASA
Congruence
4cm
4cm
78°
78°
47°
47°
Are these triangles congruent?
For triangles to be congruent, three
properties must be the same:
RHS
Congruence
4cm
4cm
5cm
5cm
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Are these triangles congruent?
Diagram
NOT
accurately drawn
Triangle
PQR
is isosceles with
PQ
=
PR
.
X
is a point on
PQ
.
Y
is a point on
PR
.
PX
=
PY
.
Prove that triangle
PQY
is
congruent to triangle
PRX
(Total 3 marks)
PX = PY (as in question)
PR = PQ (isosceles triangle)
Angles RPQ = QPR (same angle)
SAS proves triangles are congruent.
Answers
Work in pairs using the answers to
decide how many marks you would award
yourself for each question.
Plenary
Create your own question on proving
congruence or similarity.
Make sure you have provided enough
information on your diagram.
Delve into the principles of congruent triangles by exploring the properties of side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), and right-angle-hypotenuse-side (RHS) congruence. Visual explanations help clarify how these properties determine if triangles are congruent.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
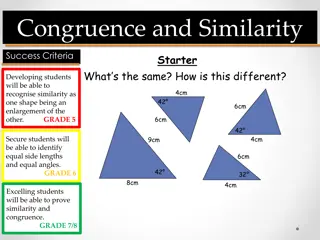
Starter What s the same? What s different? 4cm 42 6cm 6cm 42 4cm 9cm 6cm 42 32 8cm 4cm
Definitions Congruent shapes have all sides and angles equal. Similar shapes have all angles equal but one is an enlargement of the other.
Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: SSS 6cm 4cm 6cm 3.5cm 4cm 3.5cm
Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: SAS 4cm 3.5cm 78 78 4cm 3.5cm
Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: ASA 4cm 47 78 47 78 4cm
Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: RHS 5cm 5cm 4cm 4cm
P Diagram NOT accurately drawn Triangle PQR is isosceles with PQ = PR. X is a point on PQ. Y is a point on PR. PX = PY. Prove that triangle PQY is congruent to triangle PRX (Total 3 marks) Y X R Q PX = PY (as in question) PR = PQ (isosceles triangle) Angles RPQ = QPR (same angle) SAS proves triangles are congruent.
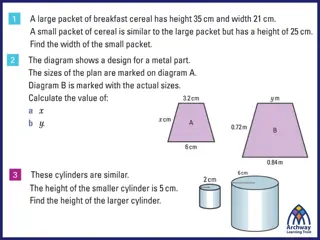
Answers Work in pairs using the answers to decide how many marks you would award yourself for each question.
Plenary Create your own question on proving congruence or similarity. Make sure you have provided enough information on your diagram.
