Parallel Vectorized Algebraic AES in Matlab for Rapid Prototyping

Implementing a Parallel Vectorized Algebraic AES in Matlab for efficient prototyping of encrypted sensor algorithms and database analytics, sponsored by the Assistant Secretary of Defense. This work focuses on the Internet-of-Things challenges, architectures, defense challenges, and current defense approaches in the context of rapidly evolving technologies and increasing interconnected devices.

• Matlab
• Encryption
• Sensor Algorithms
• Database Analytics
• Internet-of-Things

younisso Follow

Uploaded on Dec 14, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Parallel Vectorized Algebraic AES in Matlab for Rapid Prototyping of Encrypted Sensor Algorithms and Database Analytics Jeremy Kepner, Vijay Gadepally Pete Michaleas, Elizabeth Michel This work is sponsored by the Assistant Secretary of Defense for Research and Engineering under Air Force Contract #FA8721-05-C-0002. Opinions, interpretations, recommendations and conclusions are those of the authors and are not necessarily endorsed by the United States Government. UNCLASSIFIED

2. Outline Internet-of-Things Challenge Approach Implementation Results Summary Slide - 2

3. Internet-of-Things Challenge Kids Adults Elderly Humans (deciders) Rapidly increasing - Devices (1012) - Diversity (1010) - Defenses (108) Things Gap Humans 10 Years Ago 5 Years Ago Today In 5 Years Things (providers) Building Security Building Environment Building Usage Commuter Vehicles Work Vehicles Transport Vehicles Student Smartphones Classroom Tablets Fitness Wearables Slide - 3

4. Internet-of-Things Architecture Kids Adults Elderly Humans (deciders) Web Databases Ingest & Enrichment Enrichment Ingest Ingest & Analytics B A C Raw Data D E Scheduler Computing Things (providers) Building Security Building Environment Building Usage Commuter Vehicles Work Vehicles Transport Vehicles Student Smartphones Classroom Tablets Fitness Wearables Slide - 4

5. Internet-of-Things Defense Challenge Kids Adults Elderly Humans (deciders) External Denial Of Service Credential Stealing Cross VM Side Channels Remote Code Injection Web Databases Ingest & Enrichment Enrichment Ingest Ingest & Analytics B A C Raw Data Data Integrity Insider Threat Data Loss / Exfiltration D E Data Integrity Attack Scheduler Hypervisor Privilege Escalation Internal Network Resource Attacks Computing Things (providers) Supply Chain Building Security Building Environment Building Usage Commuter Vehicles Work Vehicles Transport Vehicles Student Smartphones Classroom Tablets Fitness Wearables Slide - 5

6. Current Defense Approaches - Encrypted Links and Storage - Kids Adults Elderly Humans (deciders) Encrypted link Web Databases Ingest & Enrichment Enrichment Ingest Ingest & Analytics B A C Raw Data D E Encrypted storage Encrypted storage Scheduler Computing Encrypted link Encrypted link Things (providers) Building Security Building Environment Building Usage Commuter Vehicles Work Vehicles Transport Vehicles Student Smartphones Classroom Tablets Fitness Wearables Slide - 6

7. Future Vision - Secure Algorithms & Analytics - Kids Adults Elderly Humans (deciders) Compute on Encrypted Data Web Compute on Encrypted Data Databases Ingest & Enrichment Enrichment Ingest Ingest & Analytics B A Compute on Encrypted Data C Raw Data D E Scheduler Computing Things (providers) Building Security Building Environment Building Usage Commuter Vehicles Work Vehicles Transport Vehicles Student Smartphones Classroom Tablets Fitness Wearables Slide - 7

8. Outline Internet-of-Things Challenge Approach Implementation Results Summary Slide - 8

9. Many Techniques Sensor Algorithms Filter Correlate Detect Summarize Encrypted Computation Homomorphic Fully Homomorphic Multi-Party Computation Compute on Masked Data Database Analytics Select Join Graph Cluster Encrypted Query Deterministic Order Preserving Onion Privacy Preserving Secure algorithms and analytics requires co-design with encrypted computation and encrypted query Slide - 9

10. Current Design Approach: Separate Processes & Tools Sensor Algorithms Signal-to-Noise PD vs PFA Linear Algebra Matlab Encrypted Computation Adversary Model Leakage Galois Fields Python Database Analytics Ingest Rate Query Latency Set Theory SQL Encrypted Query Adversary Model Leakage Galois Fields SQL Currently these areas have few common processes or tools Different design criteria, mathematics, and programming PD = Probability of Detection PFA= Probability of False Alarm Slide - 10

11. Our Vision: Unified Mathematics Sensor Algorithms Signal-to-Noise PD vs PFA Associative Arrays Any Language Encrypted Computation Adversary Model Leakage Associative Arrays Any Language Database Analytics Ingest Rate Query Latency Associative Arrays Any Language Encrypted Query Adversary Model Leakage Associative Arrays Any Language Associative arrays generalize the mathematics of these areas Enables co-design to occur in any programming language PD = Probability of Detection PFA= Probability of False Alarm Slide - 11

12. Prior Work Associative array mathematics unifies sensor algorithms and database analytics Perspectives on Defense Systems Analysis Mathematics of Big Data Spreadsheets, Databases, Matrices, and Graphs The What, the Why, and the Who, but Mostly the How of Broad Defense Systems Analysis William P. Delaney Jeremy Kepner and Hayden Jansen Computing on Masked Data has demonstrated encrypted computation and query using external encryption libraries* Next step: integrate encryption mathematics (Galois Fields) directly in associative array environment MIT LINCO LN LABO RATO RY SERIES MIT LINCOLN LABORATORY BOOK SERIES SIAM SOFTWARE ENVIRONMENTS TOOLS Slide - 12 *Computing on Masked Data: a High Performance Method for Improving Big Data Veracity, J. Kepner, V. Gadepally, P. Michaleas, N. Schear, M. Varia, A. Yerukhimovich, R Cunningham, IEEE HPEC 2014

13. Outline Internet-of-Things Challenge Approach Implementation Results Summary Slide - 13

14. Implementation Goals Easy-to-understand Easy to blend algorithms, analytics, and encryption mathematics Approach: use high level Galois Field mathematics found in Mathworks Communication Toolbox Good performance on many short messages Standard encryption focuses on one long message Approach: vectorize operations to encrypt/decrypt many messages using different keys at one time Good overall performance Algorithm and analytic development requires ability to test on significant data Approach: parallel implementation Demonstrate via AES CBC mode implementation Slide - 14

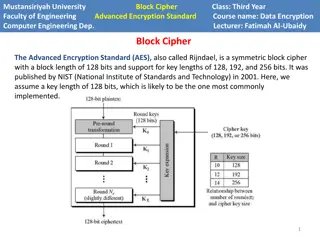
15. Advanced Encryption Standard (AES) Specification established by U.S. National Institute of Standards and Technology (NIST) in 2001 Based on the Rijndael developed by Joan Daemen and Vincent Rijmen Rijndael is a family of ciphers with different key sizes, block sizes, and modes Block: 128 bit Keys: 128 bit, 192 bit, 256 bit Modes: Electronic Codebook (ECB), Cipher Block Chaining (CBC), The Design of Rijndael: AES - The Advanced Encryption Standard, J. Daemen & V. Rijmen, Springer-Verlag, 2002 Slide - 15

16. Galois Fields 101 Represents 8 bit binary data as the coefficients of a polynomial 00000001 = 1 00000011 = x + 1 00000111 = x2 + x + 1 00001111 = x3 + x2 + x + 1 00011111 = x4 + x3 + x2 + x + 1 00111111 = x5 + x4 + x3 + x2 + x + 1 01111111 = x6 + x5 + x4 + x3 + x2 + x + 1 11111111 = x7 + x6 + x5 + x4 + x3 + x2 + x + 1 100011011 = x8 + x4 + x3 + x + 1 (AES Polynomial) All addition and multiplication in AES is done using polynomial arithmetic modulo the AES polynomial Historically, this is very tricky to implement and verify Now comes built into the Matlab Communication Toolbox Slide - 16

17. AES CBC Mathematics P, C : GF8bN M V : GF8bN 16 K : GF8bR N 16 s : GF8b256 M : GF8b4 4 i = [1:16] for each block of i columns C(:,i) = P(:,i) + V + K(1,:,:) for each round r C(:,i) = s( C(:,i) + 1) C(:,i1) = C(:,i2) C(:,1:4) = (MC(:,1:4)T)T C(:,13:16) = (MC(:,13:16)T)T C(:,i) = C(:,i) + K(r,:,:) V = C(:,i) i = i + 16 Matrix of plaintexts/ciphertexts in 8bit Galois Field Matrix of initialization vectors in 8bit Galois Field Tensor of key schedules in 8bit Galois Field s-box in 8bit Galois Field Mix matrix in 8bit Galois Field Set of 16 columns Add initialization vector and round key Majority of computation Apply s-box Shift columns Multiply by M Add round key Copy back to initialization vector Increment columns Slide - 17 http://www.moserware.com/2009/09/stick-figure-guide-to-advanced.html

18. Matlab AES Encrypt Implementation function ct = AESCBCencrypt(key,IV,pt) Nblock = ceil(size(pt,2)/16); % Number of 16 byte blocks for plaintext. pt(:,size(pt,2)+1:Nblock*16) = 0; % Pad plaintext to end of the last block. ct = uint8(pt); ct(:) = 0; % Allocate ciphertext. Nround = 10; % Standard for 128 bit. ob_gf8 = repmat(AESfield(uint8(IV)), size(pt,1), 1); % Set up IV. sbox = genSbox(); % Compute sbox from first principles. row = [2 3 1 1]; % Define mix matrix. mixmat_gf8 = gallery('circul', row); key_schedule = genKeys(key, Nround, sbox); % Generate the key schedule. idx = 1:16; for iblock=1:Nblock pt_gf8 = AESfield(pt(:,idx)) + ob_gf8; % XOR plaintext with the IV. ctrnd00_gf8 = pt_gf8 + repmat(key_schedule(1,:), size(pt_gf8,1),1); % Add plaintext and key. for iround=1:Nround ctrnd01_gf8 = AESfield(sbox(uint32(ctrnd00_gf8)+1)); ctrnd01_gf8(:,[2 3 4 6 7 8 10 11 12 14 15 16]) = ctrnd01_gf8(:,[6 11 16 10 15 4 14 3 8 2 7 12]); if (iround < Nround) % MixColumns ctrnd01_gf8(:, 1:4 ) = (mixmat_gf8 * ctrnd01_gf8(:, 1:4 ).'). ; ctrnd01_gf8(:, 5:8 ) = (mixmat_gf8 * ctrnd01_gf8(:, 5:8 ).'). ; ctrnd01_gf8(:, 9:12) = (mixmat_gf8 * ctrnd01_gf8(:, 9:12).'). ; ctrnd01_gf8(:,13:16) = (mixmat_gf8 * ctrnd01_gf8(:,13:16).'). ; end ctrnd01_gf8 = ctrnd01_gf8 + repmat(key_schedule(iround+1,:),size(pt_gf8,1),1); % AddRoundKey ctrnd00_gf8 = ctrnd01_gf8; % Copy 01 variable to 00 variable for CBC mode. end ob_gf8 = ctrnd01_gf8; % Last ciphertext becomes the IV for the next block. ct(:,idx) = reshape(uint8(uint32(ctrnd01_gf8)), size(pt,1), []); % Save current block of ciphertext. idx = idx + 16; % Increment to the next block. end Very compact implementation % SubBytes % ShiftRows Majority of computation Slide - 18

19. Outline Internet-of-Things Challenge Approach Implementation Results Summary Slide - 19

20. Code Metrics +13K C SSL Matlab/C SSL [Gadepally 2015] Matlab [Matejka 2011] Matlab [Bucholz 2001] Comm Toolbox 0 200 400 Code Volume (source lines of code) 600 800 1000 1200 Matlab AES implementation is smaller than C AES implementation Matlab is designed for rapid algorithm prototyping C is designed for high performance deployed code Using Communication Toolbox reduces code volume another 3x [Matejka 2011] http://radio.feld.cvut.cz/personal/matejka/wiki/doku.php?id=root:en:projects [Bucholz 2001] http://buchholz.hs-bremen.de/aes/aes.htm [Gadepally 2015] Improving the Veracity of Homeland Security Big Data Through Computing on Masked Data, IEEE HST 2015 Slide - 20

21. Performance vs Data Size Matlab Communication Toolbox implementation designed for high performance on many small messages (Nx16) Slide - 21

22. Comparative Performance 10x 4.1 MB/s C SSL [Gadepally 2015] 100x 2.8 KB/s Matlab [Bucholz 2001] [Matejka 2011] Other AES Matlab implementations designed purely for illustration or performance Slide - 22

23. Encrypt Parallel Performance 32 16 8 Speedup 4 2 1 1 2 4 8 16 32 Number of Cores Easy to encrypt different messages with different cores Compute intensive (little memory bandwidth contention) Slide - 23

24. Summary and Future Work Matlab Communication Toolbox AES implementation demonstrated all design goals Easy-to-understand: highly compact implementation directly maps on to matrix linear algebra widely used in sensor processing Good performance on small messages: 100x better than prior implementations Good overall performance: parallel implementation is capable of accelerating by another 20x on a single compute node Enables common environment for the development of secure sensor algorithms and secure database analytics Future Work More complex modes require more than the 32bit Galois Field supported by the Communication Toolbox 50x higher Galois Field matrix multiply performance should be possible as demonstrated by Magma Computational Algebra system* *Personal Communication, Drew Sutherland Slide - 24