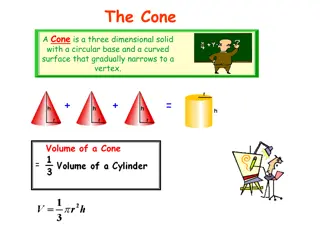
Geometric series
20 February 2025
LO: Calculate the sum of the first
n
terms in a
geometric series
Geometric series
A
geometric series
is the addition of successive terms of
a geometric sequence.
1, 2, 4, 8, 16, … ,1024 is a sequence
For example:
Sum of a finite geometric series
u
1
S
n
=
u
1
r
u
1
r
2
u
1
r
n-1
u
1
r
n-2
u
1
r
n-3
+
+
+
+
+ …… +
If
u
1
is the first term,
r
is the common ratio and
n
is the
number of terms in the series,
the last term will be
The sum of the first
n
terms can now be written as:
the second term will be:
the third term will be
the penultimate term will be
the antepenultimate term will be
u
1
r
n
rS
n
=
u
1
r
u
1
r
2
u
1
r
n-1
u
1
r
n-2
+
+
+
+ …… +
u
1
r
3
+
Multiplying by
r
Move the lower row 1 place to the right
Subtracting the expressions gives
u
1
r
n-3
+
u
1
S
n
- rS
n
=
- u
1
r
n
u
1
S
n
- rS
n
=
- u
1
r
n
The sum of a geometric series
The sum of a geometric series
u
1
S
n
– rS
n
=
– u
1
r
n
u
1
S
n
(1
– r
) =
(1
– r
n
)
u
1
S
n
=
(1
– r
n
)
(1
– r
)
u
1
S
n
=
(
r
n
–
1
)
(
r –
1)
This formula gives a negative denominator if
r
> 1
We are going to look for a formula that give us a positive
value, we can subtract the first row from the second one
Removing the common factor
Making
S
n
the subject
u
1
S
n
=
u
1
r
u
1
r
2
u
1
r
n-1
u
1
r
n-2
u
1
r
n-3
+
+
+
+
+ …… +
u
1
r
n
rS
n
=
u
1
r
u
1
r
2
u
1
r
n-1
u
1
r
n-2
+
+
+
+ …… +
u
1
r
n-3
+
-u
1
rS
n
-S
n
=
+
u
1
r
n
u
1
S
n
(
r
–
1) =
(
r
n
–
1
)
u
1
r
n
rS
n
–S
n
=
– u
1
Find the sum of the first 12 terms of the geometric series
2 + 6 + 18 + 54 + …
Because
r
> 1 we can use:
This series is geometric with
u
1
= 2,
r
= 3and
n
= 12.
=
531 440
u
1
S
n
=
(1
– r
n
)
(1
– r
)
u
1
S
n
=
(
r
n
–
1
)
(
r –
1)
S
n
=
(
r
n
–
1
)
(
r –
1)
u
1
S
n
=
(3
12
–
1
)
(
3
–
1)
2
The sum of a geometric series
Find the sum of the first 10 terms of the geometric series
4 - 2 + 1 +
…
Because
r
< 1 we can use:
This series is geometric with
u
1
= 4,
r
= -0.5 and
n
= 10.
=
2.664
u
1
S
n
=
(1
– r
n
)
(1
– r
)
u
1
S
n
=
(
r
n
–
1
)
(
r –
1)
u
1
S
n
=
(1
– r
n
)
(1
– r
)
4
S
n
=
(1
–
(
–
0.5)
10
)
(1
–
(
–
0.5))
The sum of a geometric series
Find a formula for the first n terms of
9
- 3 + 1 -
…
The series is geometric with
u
1
= 9 and
r
= -
u
1
S
n
=
(1
– r
n
)
(1
– r
)
u
1
S
n
=
(
r
n
–
1
)
(
r –
1)
u
1
S
n
=
(1
– r
n
)
(1
– r
)
9
S
n
=
(1
–
(
–
)
)
(1
–
(
–
)
)
n
9
(1
–
(
–
)
)
n
(1
–
(
–
)
)
S
n
=
=
n
Using this formula:
The sum of a geometric series
A geometric sequence has first term 5 and common ratio 2.
The sum of the first n terms of the sequence is 635.
Find n.
The sequence is geometric with
u
1
= 5 and
r
= 2.
u
1
S
n
=
(1
– r
n
)
(1
– r
)
u
1
S
n
=
(
r
n
–
1
)
(
r –
1)
S
n
=
(
r
n
–
1
)
(
r –
1)
u
1
635
=
(2
n
–
1
)
(
2
–
1)
5
(2
n
–
1
)
5
635
=
The sum of a geometric series
We need to find n such that 5
(2
n
–
1
)
= 635
Using a GDC
We are going to use a Graphing display calculator to solve the
problem
Texas Instruments
A geometric sequence has first term 5 and common ratio 2.
The sum of the first n terms of the sequence is 635.
Find
n
.
We need to find
n
such that 5
(2
n
–
1
)
= 635
Using
the GDC
: TI-84 Plus
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
We need to find
n
such that
5
(2
n
–
1
)
= 635
T
y
p
e
i
n
Y
1
=
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
E
N
T
E
R
Using
the GDC
: TI-84 Plus
We need to find
n
such that
5
(2
n
–
1
)
= 635
^
x
–
1
)
2
(
5
P
r
e
s
s
2
n
d
W
I
N
D
O
W
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
Using
the GDC
: TI-84 Plus
We need to find
n
such that
5
(2
n
–
1
)
= 635
T
y
p
e
i
n
Y
1
=
E
N
T
E
R
^
x
–
1
)
2
(
5
State the number you want to start with
T
h
e
T
b
l
i
s
t
h
e
c
h
a
n
g
e
i
n
t
h
e
t
a
b
l
e
,
I
s
e
t
1
P
r
e
s
s
2
n
d
W
I
N
D
O
W
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
I
w
a
n
t
t
o
s
t
a
r
t
i
n
1
.
E
X
E
W
e
h
a
v
e
t
w
o
o
p
t
i
o
n
s
f
o
r
t
h
e
i
n
d
e
p
e
n
d
e
n
t
a
n
d
d
e
p
e
n
d
e
n
t
v
a
r
i
a
b
l
e
:
A
u
t
o
a
n
d
A
s
k
P
r
e
s
s
2
n
d
G
R
A
P
H
Using
the GDC
: TI-84 Plus
I
l
e
a
v
e
b
o
t
h
i
n
A
u
t
o
We need to find
n
such that
5
(2
n
–
1
)
= 635
T
y
p
e
i
n
Y
1
=
E
N
T
E
R
^
x
–
1
)
2
(
5
Scroll down until you find 635 for Y
State the number you want to start with
T
h
e
T
b
l
i
s
t
h
e
c
h
a
n
g
e
i
n
t
h
e
t
a
b
l
e
,
I
s
e
t
1
P
r
e
s
s
2
n
d
W
I
N
D
O
W
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
I
w
a
n
t
t
o
s
t
a
r
t
i
n
1
.
E
X
E
P
r
e
s
s
2
n
d
G
R
A
P
H
W
e
h
a
v
e
t
w
o
o
p
t
i
o
n
s
f
o
r
t
h
e
i
n
d
e
p
e
n
d
e
n
t
a
n
d
d
e
p
e
n
d
e
n
t
v
a
r
i
a
b
l
e
:
A
u
t
o
a
n
d
A
s
k
Using
the GDC
: TI-84 Plus
I
l
e
a
v
e
b
o
t
h
i
n
A
u
t
o
We need to find
n
such that
5
(2
n
–
1
)
= 635
T
y
p
e
i
n
Y
1
=
E
N
T
E
R
^
x
–
1
)
2
(
5
Scroll down until you find 635 for Y
State the number you want to start with
T
h
e
T
b
l
i
s
t
h
e
c
h
a
n
g
e
i
n
t
h
e
t
a
b
l
e
,
I
s
e
t
1
P
r
e
s
s
2
n
d
W
I
N
D
O
W
T
u
r
n
o
n
t
h
e
c
a
l
c
u
l
a
t
o
r
P
r
e
s
s
Y
=
I
w
a
n
t
t
o
s
t
a
r
t
i
n
1
.
E
X
E
P
r
e
s
s
2
n
d
G
R
A
P
H
W
e
h
a
v
e
t
w
o
o
p
t
i
o
n
s
f
o
r
t
h
e
i
n
d
e
p
e
n
d
e
n
t
a
n
d
d
e
p
e
n
d
e
n
t
v
a
r
i
a
b
l
e
:
A
u
t
o
a
n
d
A
s
k
Using
the GDC
: TI-84 Plus
I
l
e
a
v
e
b
o
t
h
i
n
A
u
t
o
We need to find
n
such that
5
(2
n
–
1
)
= 635
T
y
p
e
i
n
Y
1
=
E
N
T
E
R
^
x
–
1
)
2
(
5
So,
S
7
= 635
n
= 7
Thank you for using resources from
https://www.mathssupport.org
If you have a special request, drop us an email
info@mathssupport.org
For more resources visit our website
A geometric series involves the sum of successive terms in a geometric sequence. By understanding the formula and principles behind geometric series, you can efficiently calculate the sum of the first n terms. Explore examples and formulas to find solutions for different series, whether the common ratio is greater than or less than 1. Learn how to apply the formulas to find the sum of geometric series effectively.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
20 February 2025 Geometric series LO: Calculate the sum of the first n terms in a geometric series www.mathssupport.org www.mathssupport.org
The sum of a geometric series A geometric series is the addition of successive terms of a geometric sequence. For example: 1, 2, 4, 8, 16, ,1024 is a sequence 1 + 2 + 4 + 8 + 16 + + 1024 is a series. Sum of a finite geometric series If u1 is the first term, r is the common ratio and n is the number of terms in the series, the last term will be The sum of the first n terms can now be written as: the second term will be: the third term will be the penultimate term will be the antepenultimate term will be while: u1rn-3 u1rn-2 u1 rn-3 + + u1rn-2 u1 rn-1 + + + + + + + + + + + u1r2 u1r3 u1r u1r2 Sn = rSn =u1r u1 u1 rn-1 u1 rn Sn - rSn = u1 - u1 rn Multiplying by r Move the lower row 1 place to the right Subtracting the expressions gives u1 Sn - rSn = - u1 rn www.mathssupport.org www.mathssupport.org
The sum of a geometric series Sn rSn = Sn(1 r) = u1 u1 u1 rn (1 rn) Removing the common factor Making Sn the subject (1 rn) u1 (1 r) Sn= This formula gives a negative denominator if r > 1 We are going to look for a formula that give us a positive value, we can subtract the first row from the second one u1 Sn = rSn = + u1rn-3 u1rn-2 u1rn-2 + + + + + + + + + + u1 rn-3 u1r2 u1r2 u1r u1r u1 rn-1 u1 rn-1 + u1 rn + u1 rn rSn-Sn= -u1 (rn 1) Sn(r 1) = u1 rSn Sn= u1rn u1 (rn 1) u1 (r 1) Sn= www.mathssupport.org www.mathssupport.org
The sum of a geometric series (rn 1) (1 rn) u1 (r 1) u1 (1 r) Sn= Sn= Find the sum of the first 12 terms of the geometric series 2 + 6 + 18 + 54 + This series is geometric with u1 = 2, r = 3and n = 12. Because r > 1 we can use: (rn 1) (r 1) (312 1) (3 1) u1 Sn= 2 Sn= = 531 440 www.mathssupport.org www.mathssupport.org
The sum of a geometric series (rn 1) (1 rn) u1 (r 1) u1 (1 r) Sn= Sn= Find the sum of the first 10 terms of the geometric series 4 - 2 + 1 + This series is geometric with u1 = 4, r = -0.5 and n = 10. Because r < 1 we can use: (1 rn) u1 (1 r) Sn= (1 ( 0.5)10) 4 (1 ( 0.5)) Sn= = 2.664 www.mathssupport.org www.mathssupport.org
The sum of a geometric series (rn 1) (1 rn) u1 (r 1) u1 (1 r) Sn= Sn= Find a formula for the first n terms of 9 - 3 + 1 - 1 3 1 3 The series is geometric with u1 = 9 and r = - Using this formula: (1 rn) u1 (1 r) (1 ( ) ) (1 ( )) Sn= 9(1 ( ) ) 4 3 1 3 n 1 3 n 9 = Sn= 1 3 (1 ( ) ) 1 3 n 27 4 Sn= www.mathssupport.org www.mathssupport.org
The sum of a geometric series (rn 1) (1 rn) u1 (r 1) u1 (1 r) Sn= Sn= A geometric sequence has first term 5 and common ratio 2. The sum of the first n terms of the sequence is 635. Find n. The sequence is geometric with u1 = 5 and r = 2. (rn 1) (r 1) (2n 1) (2 1) u1 Sn= 5 635= 635= (2n 1) 5 We need to find n such that 5(2n 1) = 635 www.mathssupport.org www.mathssupport.org
Using a GDC A geometric sequence has first term 5 and common ratio 2. The sum of the first n terms of the sequence is 635. Find n. We need to find n such that 5(2n 1) = 635 We are going to use a Graphing display calculator to solve the problem Texas Instruments www.mathssupport.org www.mathssupport.org
Usingthe GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Press Y = www.mathssupport.org www.mathssupport.org
Using the GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Press Y = ^ ^ x 1 ) 2 5 ( Type in Y1 = ENTER www.mathssupport.org www.mathssupport.org
Using the GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Type in Y1 = Press Y = ^ ^ x 1 ) 2 5 ( ENTER Press 2nd WINDOW www.mathssupport.org www.mathssupport.org
Using the GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Type in Y1 = Press Y = ^ ^ x 1 ) 2 5 ( ENTER Press 2nd WINDOW State the number you want to start with I want to start in 1. EXE The Tbl is the change in the table, I set 1 We have two options for the independent and dependent variable: Auto and Ask I leave both in Auto Press 2nd GRAPH www.mathssupport.org www.mathssupport.org
Using the GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Type in Y1 = Press Y = ^ ^ x 1 ) 2 5 ( ENTER Press 2nd WINDOW State the number you want to start with I want to start in 1. EXE The Tbl is the change in the table, I set 1 We have two options for the independent and dependent variable: Auto and Ask I leave both in Auto Press 2nd GRAPH Scroll down until you find 635 for Y www.mathssupport.org www.mathssupport.org
Using the GDC: TI-84 Plus We need to find n such that 5(2n 1) = 635 Turn on the calculator Type in Y1 = Press Y = ^ ^ x 1 ) 2 5 ( ENTER Press 2nd WINDOW State the number you want to start with I want to start in 1. EXE The Tbl is the change in the table, I set 1 We have two options for the independent and dependent variable: Auto and Ask I leave both in Auto Press 2nd GRAPH Scroll down until you find 635 for Y So, S7 = 635 n = 7 www.mathssupport.org www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org www.mathssupport.org www.mathssupport.org
