Solving Bearings and Geometric Problems
This content discusses solving problems involving bearings, geometric shapes, and properties of triangles and lines. It covers determining bearings between points, finding angles in isosceles triangles, and understanding parallel lines and angles. The content also includes information on angles in quadrilaterals and the properties of angles in different geometric configurations.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
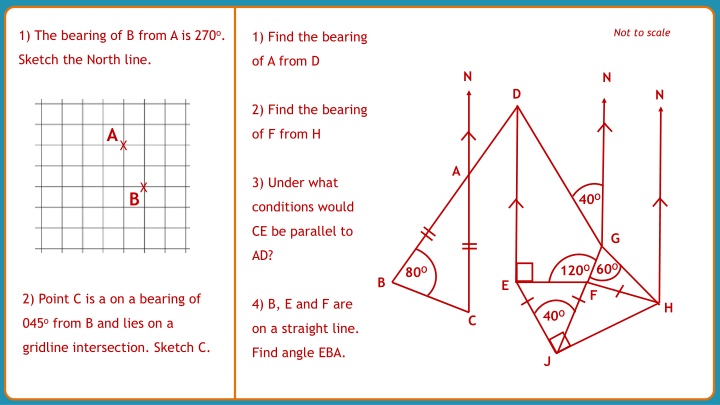
Not to scale 1) The bearing of B from A is 270o. 1) Find the bearing Sketch the North line. of A from D N N D N 2) Find the bearing A of F from H X A 3) Under what X B 40O conditions would CE be parallel to G AD? 60O 120O 80O B E F 2) Point C is a on a bearing of 4) B, E and F are H 40O C 045o from B and lies on a on a straight line. gridline intersection. Sketch C. Find angle EBA. J
1) The bearing of A from B is 3) The bearing of A from B is 5) The bearing of A from B is 180o. Sketch the North line. 180o. Sketch the North line. 180o. Sketch the North line. A B X X B X X X B A X A 2) Point C is a on a 4) Point C is a on a 6) Point C is a on a bearing of 045o from B bearing of 045o from B bearing of 045o from B and lies on a gridline and lies on a gridline and lies on a gridline intersection. Sketch C. intersection. Sketch C. intersection. Sketch C.
1) The bearing of A from B is 3) The bearing of A from B is 5) The bearing of A from B is 180o. Sketch A and B. 180o. Sketch A and B. 180o. Sketch A and B. N N N 2) Point C is a on a 4) Point C is a on a 6) Point C is a on a bearing of 045o from B bearing of 045o from B bearing of 045o from B and lies on a gridline and lies on a gridline and lies on a gridline intersection. Sketch C. intersection. Sketch C. intersection. Sketch C.
1) The bearing of A from B is 3) The bearing of A from B is 5) The bearing of A from B is 180o. Sketch a North line and B. 180o. Sketch a different North 180o. Sketch a North line and B. line and B from question 1. A A A X X X 2) Point C is a on a bearing of 4) Point C is a on a bearing of 6) Point C is a on a bearing of 045o from B and lies on a 045o from B and lies on a gridline 045o from B. Sketch C as such gridline intersection. Sketch C. intersection. Sketch C as such that ABC is an isosceles that AC>AB>BC. triangle. (With compass/ruler)
1) The bearing of A from B is 1) The bearing of A from B is 1) The bearing of A from B is 180o. Sketch a North line and B. 180o. Sketch A and B. 180o. Sketch the North line. A X A X X B N 2) Point C is a on a 2) Point C is a on a 2) Point C is a on a bearing of 045o from B bearing of 045o from B bearing of 045o from B and lies on a gridline and lies on a gridline and lies on a gridline intersection. Sketch C. intersection. Sketch C. intersection. Sketch C.
Not to scale Properties of isosceles triangles N N Sum of interior angles in a triangle D N Alternate angles in parallel lines North lines being parallel Bearings measured clockwise (& 3 figures) A Right-angles denoted by squares 40O Sum of interior angles in a quadrilateral Subtracting overlapping angles sums G Sum of angles in a full turn 120O60O 80O B E Co-interior/allied angle sums on parallel lines F H 40O Properties of parallelograms C Filtering out irrelevant angles J
