Geometric Formulas for Area of Various Shapes
Explore formulas for finding the area of different geometric shapes such as triangles, parallelograms, rhombuses, kites, and more. Learn how to calculate areas efficiently and apply them to solve problems with units. Utilize diagrams and examples to grasp the concepts effectively.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Volume of Solids Area of Any Triangle Area of Parallelogram Area of Kite & Rhombus Area of Trapezium Composite Area Volume & Surface Area Surface Area of a Cylinder Volume of a Cylinder Composite Volume Exam Type Questions
Simple Areas Definition : Area is how much space a shape takes up A few types of special Areas Any Type of Triangle Parallelogram Rhombus and kite Trapezium 2
Any Triangle Area Learning Intention Success Criteria 1. To know the formula for the 1. To develop a formula for the area of ANY triangle. area of ANY triangle. 2. Apply formula correctly. (showing working) 2. Use the formula to solve problems. 3. Answer containing appropriate units 3
Any Triangle Area h = vertical height Sometimes called the altitude h b 1 2 Area b h = 4
Any Triangle Area Example 2 : Find the area of the triangle. Altitude h outside triangle this time. 1 2 Area b h = 1 2 20 10cm Area 4 10 = Area cm 2 = 4cm 5
Any Triangle Area Pythagoras Theorem first ! Hint : Use Example 3 : Find the area of the isosceles triangle. www.mathsrevision.com a b b c 2 2 2 1 2 + + = = Area b h = 4 5 2 2 2 5cm 1 2 12 b b 5 9 4 2 2 2 Area 8 3 = = = 4cm 2 Area cm 2 = 8cm b b 9 = = 3 6
Parallelogram Area Important NOTE h h = vertical height b Parallelogram Area =b h 7
Rhombus and Kite Area Learning Intention Success Criteria 1. To know the formula for the 1. To develop a single formula for the area of ANY rhombus and Kite. area of ANY rhombus and kite. 2. Apply formulae correctly. (showing working) 2. Use the formula to solve problems. 3. Answer containing appropriate units
This part of the rhombus Area of a Rhombus is half of the small rectangle. d D Rectangle Area = (D d) 1 2 Rhombus Area= (D d) 9
Area of a Kite Exactly the same process as the rhombus d D Rectangle Area = (D d) 1 2 Kite Area= (D d) 10
Rhombus and Kite Area Example 2 : Find the area of the V shape kite. 1 2 = D d Kite Area ( ) 4cm 1 2 Area = (7 4) 7cm 2 Area = 14cm 11
Trapezium Area Learning Intention Success Criteria 1. To know the formula for the area 1. To develop a formula for the area of a trapezium. of a trapezium. 2. Apply formula correctly. (showing working) 2. Use the formula to solve problems. 3. Answer containing appropriate units 12
Trapezium Area Two triangles WXY and WYZ a cm X Y 1 1 Area 2 = 2b h Area 1 = 2a h 1 h cm 2 1 1 + Total Area = 2 2 a h b h Z W 1 2 b cm Trapezium Area = (a+b) h 13
Trapezium Area Example 1 : Find the area of the trapezium. 5cm 1 2 + Trapezium Area = ( ) a b h 4cm 1 2 + Trapezium Area = (5 6) 4 2 Trapezium Area = 22cm 6cm 14
Composite Areas Learning Intention Success Criteria 1. To show how we can apply basic area formulae to solve more complicated shapes. 1. To know the term composite. 2. To apply basic formulae to solve composite shapes. 3. Answer containing appropriate units 15
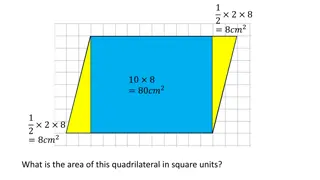
Composite Areas We can use our knowledge of the basic areas to work out more complicated shapes. Example 1 : Find the area of the arrow. l b = = 2 Rectangle Area = 3 4 12 cm 5cm 6cm 3cm 1 2 1 2 b h = 6 5 15 = 2 Triangle Area = cm 4cm 2 Total Area = 15 + 12 = 27cm 16
Composite Areas Example 2 : Find the area of the shaded area. Trapezium Area - Triangle Area 8cm 1 2 1 2 a b + Trapezium Area = ( ) h 11cm = (10 8) 11 99 + = 2 cm 4cm 1 2 1 4 11 = 2 = 22 cm Triangle Area = 2bh 10cm = 2 Shaded Area = 99 - 22 77cm 17
Summary Areas Rhombus and kite Any Type of Triangle 1 2 1 2 = D d Area ( ) Area b h = Trapezium Parallelogram = 1 2 Area = (a+b)h Area b h
Volume of Solids Prisms Learning Intention Success Criteria 1. To know the volume formula 1. To understand the prism formula for calculating volume. for any prism. 2. Work out volumes for various prisms. 3. Answer to contain appropriate units and working.
Volume of Solids Definition : A prism is a solid shape with uniform cross-section Hexagonal Prism Cylinder (circular Prism) Triangular Prism Pentagonal Prism Volume = Area of Cross section x length
Definition : A prism is a solid shape with uniform cross-section Q. Find the volume the triangular prism. Triangular Prism Volume = Area x length 3 = 20 x 10 = 200 cm 10cm 2 20cm
Volume of Solids Definition : A prism is a solid shape with uniform cross-section www.mathsrevision.com Q. Find the volume the hexagonal prism. 2 43.2cm Volume = Area x length 20cm Hexagonal Prism 3 = 43.2 x 20 = 864 cm
Net and Surface Area Triangular Prism Bottom 4cm 4cm FT BT Back 10cm 4cm Front 4cm 5 faces 3 congruent rectangles 2 congruent triangles 10cm This is a NET for the triangular prism.
Example Find the surface area of the right angle prism Working 1bh 2 Triangle Area = 2 = 2 x3 =6cm Rectangle 1 Area = l x b = 3 x10 =30cm Rectangle 2 Area = l x b = 4 x 10 =40cm Rectangle 3 Area = l x b = 5 x 10 =50cm 2 5cm 3cm 2 10cm 4cm 2 2 triangles the same 1 rectangle 3cm by 10cm 1 rectangle 4cm by 10cm 1 rectangle 5cm by 10cm Total Area = 6+6+30+40+50 = 132cm 2
Net and Surface Area The Cuboid 3cm Bottom Back LS 4cm RS 4cm Top 3cm 3cm 5cm Front 4cm 6 faces Top and bottom congruent Front and back congruent Left and right congruent 5cm This is a NET for the cuboid
Example Find the surface area of the cuboid Working Front Area = l x b 2 = 5 x 4 =20cm Top Area = l x b 2 = 5 x 3 =15cm 4cm Side Area = l x b 2 = 3 x 4 =12cm 3cm Total Area 5cm Front and back are the same Top and bottom are the same Right and left are the same = 20+20+15+15+12+12 = 94cm 2
Surface Area of a Cylinder Learning Intention Success Criteria 1. To explain how to calculate the surface area of a cylinder by using basic area. 1. To know split up a cylinder. 2. Calculate the surface area of a cylinder.
Surface Area of a Cylinder The surface area of a cylinder is made up of 2 basic shapes can you name them. Cylinder (circular Prism) 2 r Curved Area =2 rh Top Area = r2 Bottom Area = r2 h Roll out curve side Total Surface Area = 2 r2 + 2 rh
Surface Area of a Cylinder Example : Find the surface area of the cylinder below: 3cm Surface Area = 2 r2 + 2 rh 10cm = 2 (3)2 +2 x 3 x 10 = 18 + 60 = 78 cm Cylinder (circular Prism)
Surface Area of a Cylinder Diameter = 2r Example : A net of a cylinder is given below. Find the diameter of the tin and the total surface area. 2 r = 25 25 9cm 2r = 25cm Surface Area = 2 r2 + 2 rh = 2 (25/2 )2 + 2 (25/2 )x9 = 625/2 + 25x9 = 324.5 cm
Volume of a Cylinder The volume of a cylinder can be thought as being a pile of circles laid on top of each other. Volume = Area x height = r2 = r2h h x h Cylinder (circular Prism)
Volume of a Cylinder Example : Find the volume of the cylinder below. 5cm V = r2h 10cm = (5)2x10 = 250 cm Cylinder (circular Prism)
Other Simple Volumes Composite volume is simply volumes that are made up from basic volumes. r r h D h Cylinder (circular Prism) r Cylinder = r2h 4 3 Volume = r 3 1 3 Volume Cone = r h 2
Volume of Solids Prisms Learning Intention Success Criteria 1. To know what a composite 1. To calculate volumes for composite shapes using knowledge from previous sections. volume is. 2. Work out composite volumes using previous knowledge of basic prisms. 3. Answer to contain appropriate units and working.
Other Simple Volumes Composite volume is simply volumes that are made up from basic volumes. r r h D h Cylinder (circular Prism) r Cylinder = r2h 4 3 Volume = r 3 1 3 Volume Cone = r h 2
Volume of a Solid Composite volume is simply volumes that are made up from basic volumes. Q. Find the volume the composite shape. Volume = Cylinder + half a sphere 1 2 2 3 4 3 1 2 4 3 V= r h + ( r ) 2 3 = (2) 6 + ( (2) ) 2 3 16 3 88 3 r = 24 + (8) = 24 + = h = 6m 2m
Volume of a Solid Composite Volumes are simply volumes that are made up from basic volumes. Q. This child s toy is made from 2 identical cones. Calculate the total volume. Volume = 2 x cone 1 V = 2 r h 3 2 = (10) 3 2 r = 10cm h = 60cm 30 2 = 6283cm 3
