Geometric Constructions and Perpendicular Bisectors
Explore geometric constructions involving equidistance, perpendicular bisectors, and circle drawing using compasses. Learn how to find the midpoint between two points, determine the path to stay equidistant from two objects, and construct perpendicular bisectors accurately. Enhance your understanding of geometry with practical examples and step-by-step visual guides.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
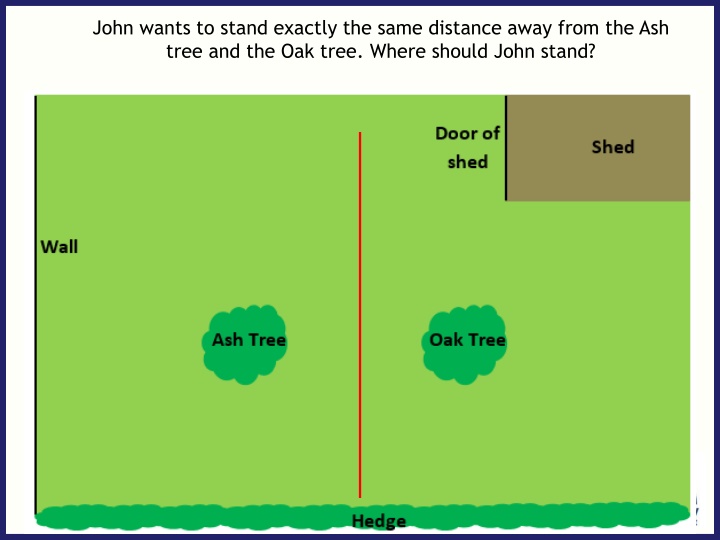
John wants to stand exactly the same distance away from the Ash tree and the Oak tree. Where should John stand?
The ship wants to keep as far away from the rocks as possible at all times. What path should the ship take? How can we represent the path that the ship should take accurately?
The ship wants to keep as far away from the rocks as possible at all times. What path should the ship take? We need to make sure the path that we draw is equidistant from the two rocks
The ship wants to keep as far away from the rocks as possible at all times. What path should the ship take? To do this we can use a construction. This is known as a perpendicular bisector. Can you think why?
The Perpendicular Bisector Perpendicular: At right angles (900) Bisector: Split into equal parts
Anchor compasses on one end of the line segment. Set the width of the compasses so that the radius is greater than half of the length of the line segment Draw a circle Do not alter the width of the compasses
Anchor compasses on the other end of the line segment. Draw a circle.
Join the two intersection points with a straight edge . This is the perpendicular bisector
Title: The Perpendicular Bisector Q1. Construct the perpendicular bisector of the following line segments Draw in your books Q2. Construct the perpendicular bisector of the line AB for each polygon.
Extension Draw a triangle and construct the perpendicular bisector of each side You should find that the bisectors intersect at a single point, either inside or outside the circle! Now using the point of intersection as centre, draw the smallest possible circle that does not enter the triangle You should find that the circle touches all three corners of the triangle This works with anytriangle
Using a compass and ruler only can you construct a 90 and 45 degree angle with a perpendicular bisector 45o angle Right-angle Draw a perpendicular bisector Bisect a 90o angle from a perpendicular bisector
