Exploring Triangles: Types, Properties, and Examples
Welcome back
Welcome back
everyone!!
everyone!!
1
T
T
r
r
i
i
a
a
n
n
g
g
l
l
e
e
s
s
a
a
n
n
d
d
t
t
y
y
p
p
e
e
s
s
o
o
f
f
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
s
s
2
W
W
h
h
a
a
t
t
i
i
s
s
a
a
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
?
?
A
B
C
A closed figure formed by joining three
l
i
n
e
s
e
g
m
e
n
t
s
i
s
c
a
l
l
e
d
a
t
r
i
a
n
g
l
e
.
3
Every triangle has 3 sides, 3 vertices and 3
angles.
A
B
C
A, B and C
are vertices.
Here, AB, BC and CA
are the three sides.
and
ABC
,
ACB are the angles.
BAC and
4
T
T
y
y
p
p
e
e
s
s
o
o
f
f
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
s
s
5
6
E
E
q
q
u
u
i
i
l
l
a
a
t
t
e
e
r
r
a
a
l
l
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
Triangles having all sides equal are called
equilateral triangle.
A
B
C
7
E
E
x
x
a
a
m
m
p
p
l
l
e
e
:
:
A
B
C
6 cm
6 cm
6 cm
Here, sides
AB = BC = CA = 6cm
8
Triangles having 2 sides equal are called isosceles
triangle.
I
I
s
s
o
o
s
s
c
c
e
e
l
l
e
e
s
s
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
A
B
C
9
E
E
x
x
a
a
m
m
p
p
l
l
e
e
:
:
A
B
C
7 cm
7 cm
4 cm
Here, sides
AB = AC = 7cm
and BC = 4cm
10
S
S
c
c
a
a
l
l
e
e
n
n
e
e
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
T
r
i
a
n
g
l
e
s
h
a
v
i
n
g
N
O
s
i
d
e
s
e
q
u
a
l
a
r
e
c
a
l
l
e
d
s
c
a
l
e
n
e
t
r
i
a
n
g
l
e
A
B
C
NO EQUAL
SIDES!
11
E
E
x
x
a
a
m
m
p
p
l
l
e
e
:
:
A
C
B
7 cm
5 cm
6 cm
12
A
A
c
c
u
u
t
t
e
e
a
a
n
n
g
g
l
l
e
e
d
d
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
Triangles whose all angles are acute are called
acute angled triangle.
13
R
R
i
i
g
g
h
h
t
t
a
a
n
n
g
g
l
l
e
e
d
d
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
Triangle whose 1 angle is right angle is called right
angled triangle.
90°
45°
45°
14
O
O
b
b
t
t
u
u
s
s
e
e
a
a
n
n
g
g
l
l
e
e
d
d
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
Triangle whose 1 angle is obtuse is called obtuse
angled triangle.
15
C
C
a
a
l
l
c
c
u
u
l
l
a
a
t
t
e
e
s
s
u
u
m
m
o
o
f
f
t
t
h
h
e
e
a
a
n
n
g
g
l
l
e
e
s
s
i
i
n
n
a
a
t
t
r
r
i
i
a
a
n
n
g
g
l
l
e
e
In any triangle,
S
u
m
o
f
t
h
e
T
h
r
e
e
A
n
g
l
e
s
=
1
8
0
°
If the sum of the three angles in a triangle is not equal to
180°, then those three angles can not be the angles of a
triangle.
62° + 75° + 43°
= 180°
16
A
n
s
w
e
r
=
7
3
°
17
18
19
20
21
22
23
24
Delve into the world of triangles through an insightful exploration of their types, properties, and examples. Learn about equilateral, isosceles, scalene, acute-angled, and right-angled triangles, along with their defining characteristics and visual representations. Enhance your understanding of geometry with clear explanations and vivid imagery.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Welcome back everyone!! 1
Triangles and types of triangles 2
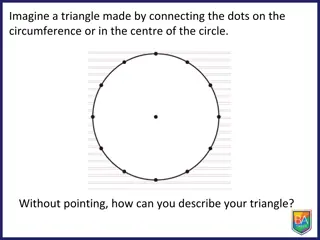
What is a triangle? A C B A closed figure formed by joining three line segments is called a triangle. 3
Every triangle has 3 sides, 3 vertices and 3 angles. A A, B and C are vertices. Here, AB, BC and CA are the three sides. B C ABC , BAC and ACB are the angles. and 4
TRIANGLES SIDES ANGLES Acute angled triangle Equilateral triangle Right angled triangle Isosceles triangle Obtuse angled triangle Scalene triangle 6
Equilateral triangle Triangles having all sides equal are called equilateral triangle. A C B 7
Example: A Here, sides AB = BC = CA = 6cm 6 cm 6 cm C B 6 cm 8
Isosceles triangle Triangles having 2 sides equal are called isosceles triangle. A B C 9
Example: A Here, sides AB = AC = 7cm and BC = 4cm 7 cm 7 cm B C 4 cm 10
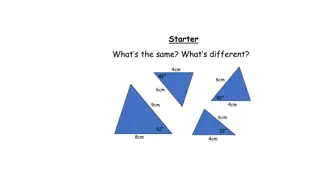
Scalene triangle Triangles having NO sides equal are called scalene triangle NO EQUAL SIDES! B A C 11
Example: B 7 cm 5 cm C A 6 cm 12
Acute angled triangle Triangles whose all angles are acute are called acute angled triangle. 13
Right angled triangle Triangle whose 1 angle is right angle is called right angled triangle. 45 90 45 14
Obtuse angled triangle Triangle whose 1 angle is obtuse is called obtuse angled triangle. 15
Calculate sum of the angles in a triangle In any triangle, Sum of the Three Angles = 180 If the sum of the three angles in a triangle is not equal to 180 , then those three angles can not be the angles of a triangle. 62 + 75 + 43 = 180 16
Answer = 73 17
