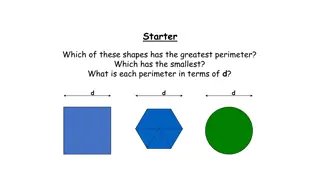
Exploring Triangles in Circles
Discover various types of triangles that can be formed by connecting dots on the circumference or in the center of a circle. Learn to classify triangles such as scalene, right-angled, isosceles, equilateral, and more based on their sides and angles. Explore methods to identify and calculate angles in different triangle configurations.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Imagine a triangle made by connecting the dots on the circumference or in the centre of the circle. Without pointing, how can you describe your triangle?
Here are some examples. How would you describe them to your partner without pointing?
How many different triangles made by connecting the dots on the circumference or in the centre of the circle can you draw? How do you know you have got them all?
Look at the types of triangle you have. How can you classify them?
Scalene triangle: Nothing special about this triangle
Right angled triangle: 1 angle of 90 Right angled isosceles triangle: 1 angle of 90 2 other equal angles
Equilateral triangle: All sides equal All angles are equal all 60 Isosceles triangle: 2 equal sides 2 equal angles
Isosceles triangle: Two equal sides, two equal angles Same legs (sides) Same feet (angles)
How do you know that this is an isosceles triangle without measuring it?
How can I find the angle at the centre in this isosceles triangle?
One student drew these lines. What calculation would they do to find the angle, x?
Another student drew these lines. What calculation would they do to find the angle, x?
Heres another way. What calculation would they do to find the angle, x?
How can I find the other angles in this isosceles triangle? 30 x x
How can I find the angles in this isosceles triangle? (Try adding some lines to help)
On your whiteboards: Find the missing angles Explain how you found the answer x 20 60 x x x
In your books: Find the missing angles
On your whiteboards: Draw an isosceles triangle with all acute angles and another
On your whiteboards: Draw an isosceles triangle with an obtuse angle and another
