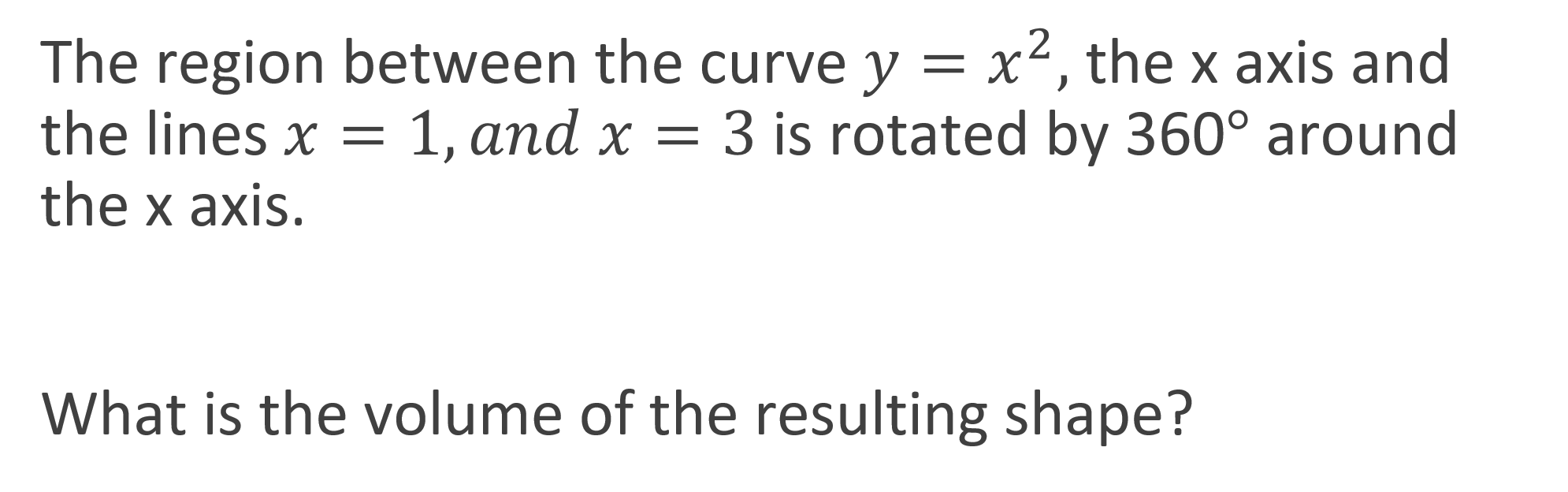Example One
examples and exercises involving rotational solids created by rotating regions around axes. Calculate volumes and areas of shapes defined by curves, lines, and axes in calculus.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Example One The region between the curve ? = ?2, the x axis and the lines ? = 1,??? ? = 3 is rotated by 360 around the x axis. What is the volume of the resulting shape? Graph
Example Two: The region R is bound by the curve with equation ? = ?2 1, the x axis and the lines ? = 0 and ? = 2. a) Calculate the area of the region R. The region R is rotated 360 about the x axis. b) Find the exact volume of the solid formed.
Revolving around the ?-axis ? To revolve instead around the ?-axis, we simply swap the roles of the ? and ? axes! If the curve is revolved around ?-axis: ? = ? ?2 ?? ? ? ?? ? ? The diagram shows the curve with equation ? = ? 1. The region ? is bounded by the curve, the ?-axis and the lines ? = 1 and ? = 3. The region is rotated through 360 about the ?-axis. Find the volume of the solid generated. ? = ?2+ 1 3 ?2+ 12 ?? ? ? = ? ? 1 = =1016? 15 ? = ? 1 3 ? 1 ?
Test Your Understanding 32? + 1. The region ? is bounded by the curve, the A curve has equation ? = ?-axis and the lines ? = 2 and ? = 4. The region is rotated through 360 about the ?-axis. Find the volume of the solid generated. ?3= 2? + 1 ? =1 2?3 1 41 2 2?3 1 ? 2 ? = ? ?? 2 2 = =7715? 14
The region R is formed by the y axis, the lines y = 0 and y = 9 and the curve with equation ? = ? + 22 a) Find the area of the region R. The region R is rotated 360 about the y axis. b) Find the volume of the solid formed.
Example ? The region ? is bounded by the curve with equation ? = ?3+ 2, the line ? = 5 2? and ? and ?-axes. (a) Verify that the coordinates of ? are 1,3 . A solid is created by rotating the region 360 about the ?-axis. (b) Find the volume of this solid. ? = ?3+ 2 ? ? = 5 2? ? ? ? ? a 13+ 2 = 3, 5 2 1 = 3 Find the two volumes separately: ? ? = ?3+ 2 1 ?3+ 22 ?? = =36? ?1= ? ? 7 0 5 2? intersects the ?-axis at 2.5 ?2=1 ? b ? = 5 2? ?1 3? 32 1.5 =9? ?2 It s a cone! ? 2 ? 2.5 1 ????????=36? +9? 2=135? 7 14
Volumes by Subtraction ? The diagram shows the region ? bounded by the curves with equations ? = ? and ? = 8? and the line ? = 1. The region is rotated through 360 about the ?-axis. Find the exact volume of the solid generated. 1 1 ? = ? = ? 8? ? Do volume under top curve and subtract volume under bottom curve. ? 1 Point of intersection: 1 8?= ? =1 3 2= 1 ? 8? 4 ? 1 ?2 ?? = =15? ?1= ? 1 32 4 2 1 1 ?? = =3? ?2= ? 1 8? 64=27? 64 4 ??=15? 32 3? 64
Test Your Understanding ? 3?, The area between the lines with equations ? = ? and ? = where ? 0 is rotated 360 about the ?-axis. Determine the volume of the solid generated. 3? ? = ? = ? ? 1 3 ?3= ? ? = ? ?3 ? = 0 ? ? 1 ? + 1 = 0 Intersect at ? = 1,0,1 ? 2 ? 1 ?? = =3? 1 3 ?1= ? ? 5 0 ?2=1 ??=3? 1 =? 3=4? 15 3? 12 5 ? 3