Computer Modeling in Physical Systems and Design Work

GEOMETRIC MODELS S.JOSEPHINE THERESA, DEPT OF CS, SJC, TRICHY-2

CONTENT A SIMPLE MODELING GEOMETRIC MODELING SYMBOLS AND INSTANCES

INTRODUCTION Most popular and effective use of digtial computer is physical system General term Modeling Computer models can be built of both physical objects and physical processes

Examples Electric Circuit Building National and world Economies Weather All these examples use computer models to help them in their design work

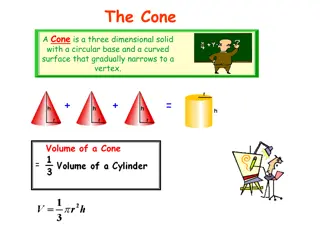
Computer model is used as a basis for simulation It is very important field of computing Number of programming languages have been designed to help simulation by making it easier to build models It is mainly used in Computer aided design Solid objects are modeled by computer

Continuation. Integrated circuits are modeled it can be checked automatically against design rule CG is associated with modeling It is very convenient way to observe the behaviour of computer models Simulate weather patterns, we can plot pressure and temperature values on a displayed map instead of printing them in a tabular form

A simple data structure representing a circuit model type x1 y1 x2 y2 x y type X y components Wire segments

Each component is defined by an element Data containing its type and coordinate position on the diagram and each line segment of a wire is defined by coordinates of its two endpoints Relational information- Connection between components- is defined by procedures We can write a procedure whether a wire and a component are connected by comparing coordinates

We can write another procedure to apply a similar connectivity test to any two wires Then applying these two procedures iteratively to the contents of the data structure we can determine which components are connected together.

A SIMPLE MODELING Many computer models consist of a mixture of data structure and procedures In few cases models of a solid objects we find a lot of data and very few procedures Circuit model is no exception to the rule It consist of a simple data structure supplemented by some procedures The data structure defines each of the components and connecting wires in the circuit diagram It does not contain any relational information

Inclusion of component definition in the model X1 Y1 X2 y2 1 2 3 X1 Y1 X2 Y2 table Component lines

Line segments are generated using the stored endpoints as parameters The display of the components is slightly more complicated This algorithm will scan the list of lines and components and display each at its apporpriate position

ALGORITHM Procedure showcomponents Var I,j; integer; xt,yt;real;c:coponent Begin For i=1 to n components do begin Xt=components[i].x Yt=components[i].y C=componenttable[component[i],comptyp]; With c do begin For j=1 to n lines do begin MoveTo(Lines[j].x1+xt,Linesj].y1yt); LineTo(Lines[j].x2+xt,Linesj].y2yt) End end end end Procedure show wires var I :integer Begin For i=1 to n wires do begin MoveTo(Wires[i].x1, wires[1],y1); LineTo(Wires[i].x2,wires[i],y2) End end;

GEOMETRIC MODELING It is in the form of circuit diagram The line segments representing each component and each connection in the circuit are fully defined by the coordinates stored in the data structure Models which have this property are called geometric models We can also construct physical model Non geometric modeling is usually applied to physical processes rather than objects

Procedure to determine the coordinates of a sequence of lines connecting two components Procedure LinkPoints(x1,y1,x2,y2:integer); Begin MoveTO((x1,y1); LineTO((x1+x2)/2,y1); LineTo((x1+x2)/2,y2); LineTo(x2,y2) end

A pair of components connected by lines generated with the LinkPoints Procedure b a

Displaying a Geometric Model A model that defines the geometric form of an object There are 3 different displayed representations of the same three dimensional object Display model objects depends on hardware and software for their display Methods are based on common features such as

Basic elements of data that typically appear as individual graphic entities on the screen Structure - Certain relationships between the basic data elements - Many different kinds of relationship can be expressed in models - Like lists, arrays, sets, rings and other kinds of structuring mechanisms

Transformation - Define the position and orientation of each part of the modeled object - When there is no repetitive use of the same component we use transformation to position the different parts of the modeled object

SYMBOLS AND INSTANCES The use of graphical symbols is very common in charts and graphs When we draw charts on a display we must be able to define symbols and multiple instances of each symbol in the chart itself Define the symbol in a different coordinate system called master coordinate system Functions are needed for the specification of instance transformations

There are three new instance transformation functions allow us to define the scaling, rotation, and translation to be applied to the symbol Scale(sx,sy) scale the symbol by factors sx and sy in the x and y directions relative to the origin Rotate(teta) Rotate the symbol through teta degrees clockwise about the origin Translate(tx,ty)- Translate the symbol through distance tx and ty measured in x y directions

Ori gin Scale(0.3,0.3) Translate(12,10) Master Coordinate Definition Rotate (45)

Steps in the transformation sequence world World coordinate System Apply viewing transformation clip Generate display code

master world Apply instance transformatio m Apply viewing transformatio n Master Coordinate data screen Generate display code clip

PICTURE STRUCTURE Geometric models and other forms of data has clear structure Structure use certain symbols, in connections drawn linking the symbols And overall organization of the displayed image

Techniques in picture Repetition - Inherent in many pictures - Repeated instances of symbols Connectivity - Pictures show the relationship between elements by means of lines and arrows connecting them

Construction - Use Transformation and symbols in constructing pictures Interaction - Dispplay file segments simplify the design of interactive programs and permit us to divide pictures .It is visible structure

DEFINING SYMBOLS BY PROCEDURES Repetitive structure in pictures use symbols to represent these structures Method of defining symbols and invoking instances of them that made use of sequences of primitive function calls