The Ultimate Guide to BMW Car Oil Change Service in Newton, HI
Embark on a journey of automotive excellence with our guide to BMW car oil change service in Newton, HI. Expert technicians, high-performance oils, and state-of-the-art facilities converge for unparalleled service. Transparent pricing, genuine BMW parts, and eco-friendly practices ensure a seamless
2 views • 22 slides
Get the Best Flu Vaccination in Newton
Get the Best Flu Vaccination in Newton at Island Medical Clinic, your trusted healthcare partner in Newton! They prioritize your well-being above all else. As a leading medical clinic in Newton, their dedicated team of healthcare professionals is committed to providing comprehensive and compassionat
0 views • 6 slides
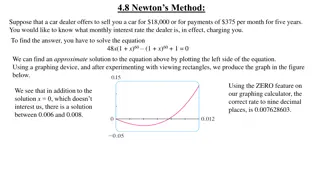
Understanding Newton's Method for Solving Equations
Newton's Method, also known as the Newton-Raphson method, is a powerful tool for approximating roots of equations. By iteratively improving initial guesses using tangent lines, this method converges towards accurate solutions. This method plays a crucial role in modern calculators and computers for
0 views • 12 slides
Understanding Mass, Motion, and Force According to Newton's Second Law
Explore the relationship between mass, motion, and force through Newton's Second Law. Learn how the mass of an object affects the force required to change its motion, illustrated with examples like hitting different balls with the same force and pulling a wagon empty vs. loaded. Dive deeper into the
0 views • 10 slides
Introduction to Arithmetic Operations on Polynomials
This unit focuses on developing an understanding of polynomials in mathematical expressions. You will learn about the parts of a polynomial, polynomial operations, and representing polynomials. The topics cover performing arithmetic operations on polynomials, identifying variables in expressions, le
1 views • 71 slides
Understanding Polynomial Functions and Operations
Polynomial functions are mathematical functions in the form of an expression involving variables and coefficients. They can be manipulated through operations like addition, subtraction, multiplication, and division. Learn about polynomial degrees, identifying polynomials, and performing various oper
0 views • 20 slides
Optimization Methods: Understanding Gradient Descent and Second Order Techniques
This content delves into the concepts of gradient descent and second-order methods in optimization. Gradient descent is a first-order method utilizing the first-order Taylor expansion, while second-order methods consider the first three terms of the multivariate Taylor series. Second-order methods l
0 views • 44 slides
Understanding Polynomial Degrees and Special Names
The degree of a polynomial is determined by its highest exponent, with specific names for each degree level. From the basic constant to the nth degree polynomial, this guide showcases the different degrees and their characteristics, helping you grasp the concept of polynomial functions easily.
0 views • 18 slides
Understanding Polynomials: Types, Degrees, and Zeroes
Polynomial expressions consist of terms with non-zero coefficients. They can have any number of terms and different degrees. Linear polynomials have a degree of one, quadratic polynomials have a degree of two, and cubic polynomials have a degree of three. Zeroes of a polynomial are the values of the
0 views • 17 slides
Understanding Newton's Third Law of Motion
Explore the concept of Newton's Third Law of Motion, which states that for every action there is an equal and opposite reaction. Discover examples illustrating this law in action and learn about inertia, unbalanced forces, and the relationship between force, mass, and acceleration according to Newto
0 views • 7 slides
Understanding Newton's Laws of Motion and Law of Universal Gravitation
Isaac Newton, a giant in scientific history, revolutionized physics with his three laws of motion and law of universal gravitation. His laws of inertia, force, and action and reaction explain the behavior of objects in motion, while the law of gravitation describes the force that governs celestial b
3 views • 10 slides
Understanding Polynomial Functions with Real Zeros
Learn how to identify and write polynomial functions that include real zeros, find zeros of given functions, explore the Fundamental Theorem of Algebra, and apply the Number of Zeros Theorem. Practice writing polynomial functions satisfying specific conditions.
0 views • 11 slides
Understanding Newton's Laws of Motion
Explore Newton's Laws of Motion including the concepts of force, inertia, acceleration, action and reaction forces, and the role of mass in determining motion. Newton's First Law states that objects at rest remain at rest unless acted upon by an unbalanced force. Newton's Second Law relates accelera
0 views • 16 slides
Understanding Newton's Laws of Motion
Explore Sir Isaac Newton's foundational principles of motion through engaging visuals and real-world examples. Discover how inertia, force, and acceleration shape the dynamics of objects in motion, as explained by Newton's First and Second Laws. Delve into the concept of inertia and the relationship
2 views • 13 slides
Empirical Successes of Newton's Theory of Gravity
Newton's theory of gravity has been empirically validated through observations such as the uniform rate of falling bodies, explanation of Kepler's laws of planetary motion, discovery of new planets, influence on tides, and more. These findings illustrate the depth of understanding achieved by Newton
0 views • 4 slides
Understanding Newton's Laws of Motion
Newton's laws of motion, including the principles of inertia and dynamics, explain how objects move and interact with forces. The first law states that objects in motion remain in motion unless acted upon by a force, while the second law explains how a net force is required to change an object's vel
0 views • 21 slides
Understanding Newton's Law of Universal Gravitation
Newton's Law of Universal Gravitation explores the concept of gravity, how it affects different bodies in space, and the relationship between mass, distance, and gravitational force. Newton's pioneering work in this area laid the foundation for understanding the forces that govern the movement of pl
0 views • 22 slides
Polynomial Long Division Review and Practice
This content provides a detailed review on polynomial long division including step-by-step instructions, examples, and synthetic division practice problems. It covers topics such as descending polynomial order, solving binomial divisors, writing coefficients, determining remainders, and obtaining fi
0 views • 4 slides
Polynomial Division Methods and Examples
Dividing polynomials involves using methods like long division or equating coefficients. By applying these techniques, you can determine whether a polynomial divides exactly or leaves a remainder. The process is similar to long division of numbers, where the dividend is divided by the divisor to obt
0 views • 10 slides
Polynomial Division and Remainder Theorems Explained
Learn how to use long division to find quotients and remainders in polynomial problems. Understand when to use long division or synthetic division. Discover how the remainder theorem works by finding remainders when dividing specific polynomials by different factors. Explore the factor theorem and i
0 views • 6 slides
The Life and Discoveries of Isaac Newton - A Journey from Birth to Legacy
A glimpse into the life of Isaac Newton, the famous scientist born in 1642 amidst turbulent times. From his premature birth to the discovery of gravity with an apple, Newton's story unfolds. Despite early hardships, his academic achievements and groundbreaking work in science marked his legacy. Expl
0 views • 9 slides
Understanding Physics Misconceptions and Newton's Laws
Cognitive scientists have shown that physics students often hold misconceptions about motion that hinder their learning. Overcoming these misconceptions involves self-reflection, critical thinking, and evaluation. Newton's laws of motion play a significant role in understanding the concepts. Questio
0 views • 56 slides
Strong List Coloring and the Polynomial Method in Graph Theory
Exploring the Polynomial Method in the context of Strong List Coloring, Group Connectivity, and Algebraic tools. This method involves proper coloring of graphs based on polynomial assignments, highlighting the significance of Strong Choosability and the Co-graphic case. The applications and proofs a
0 views • 34 slides
Understanding Polynomial Identity Testing in Algorithm Design
Explore the concept of polynomial identity testing as a powerful tool in algorithm design. Learn how to determine if a polynomial is identically zero by choosing random points and applying the Schwartz-Zippel Lemma. Discover the application of this technique in finding perfect matchings in bipartite
0 views • 26 slides
Understanding Isaac Newton's Mathematical Principles of Natural Philosophy
Dive into Isaac Newton's "Principia," where he explores the foundational principles of mechanics, motion, and geometry. Newton's work revolutionized our understanding of the physical world and laid the groundwork for modern physics.
0 views • 6 slides
Isaac Newton: Contributions to Mathematics and Physics
Isaac Newton, a renowned physicist and mathematician from England, was the greatest scientist of his era. Despite being described as 'idle' and 'inattentive' in school, he formulated the Three Laws of Motion and the law of Universal Gravitation. Newton's mathematical contributions include studying p
0 views • 16 slides
Approximating Knapsack Problem in Polynomial Time
In the recent discussion, we explored approximating the Knapsack problem in fully polynomial time. By utilizing a polynomial-time approximation scheme (PTAS), we aim to find a set of items within a weight capacity whose value is within a certain range of the optimal value. This approach involves lev
0 views • 22 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
0 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
Understanding Orbital Dynamics: From Newton's Laws to Kepler's Laws
Exploring the fascinating realm of orbital dynamics, this content delves into the application of Newton's laws to explain Kepler's laws and the intricacies of orbital mechanics. Deriving Kepler's laws from Newton's law of gravitation involves advanced mathematics, while also emphasizing the signific
0 views • 25 slides
Physics 1443 Section 003 Lecture #9 Summary and Homework Announcement
Dr. Jae Jaehoon Yu covered Newton's Laws of Motion, specifically focusing on Newton's third law, categories of forces, gravitational force, weight, and applications of Newton's laws in lecture #9. The lecture also discussed the force of friction and announced homework #5 due by 11 pm on Tuesday, Mar
0 views • 18 slides
Understanding Newton's Laws of Motion
Dynamics is governed by Newton's three fundamental laws of motion. These laws, formulated by Newton, describe the behavior of objects in motion and at rest. Key terms such as mass, weight, momentum, force, and inertia are crucial in understanding these laws. Rigid bodies, which consist of fixed part
0 views • 22 slides
Advanced Techniques in Secret Sharing Schemes
Explore the advancements in polynomial secret-sharing schemes and their applications in cryptography. Discover how polynomial schemes provide efficient solutions for sharing secrets among multiple parties while maintaining security. Learn about the construction of polynomial conditional disclosure p
0 views • 16 slides
Newton's Interpolating Polynomials in Mechanical Engineering
Explore Newton's interpolating polynomials in the context of Mechanical Engineering, specifically focusing on numerical methods and interpolation techniques. Dr. Mohamed El-Shazly, an Associate Professor of Mechanical Design and Tribology, guides students through the concepts and applications of New
0 views • 17 slides
Evolution of Scientific Thought: From Aristotle to Newton
Explore the historical perspectives of scientific giants like Aristotle, Galileo, Tycho Brahe, Kepler, and Isaac Newton, as they revolutionized our understanding of motion and the universe. Witness the shift from ancient beliefs to modern scientific principles, culminating in Newton's groundbreaking
0 views • 23 slides
Understanding Rational Functions Through Divided Differences and Newton Polynomial
Explore the mathematical approach of using divided differences and Newton Polynomial to determine an equation for a rational function passing through given points. The process involves creating a system of linear equations and utilizing Newton Polynomial to establish relationships between points. Va
0 views • 20 slides
Polynomials Operations: Adding, Subtracting, Multiplying - Unit 7 Days 1 and 2
Dive into the world of polynomial operations in this engaging unit covering adding, subtracting, and multiplying polynomials. Explore methods to combine like terms, distribute negative signs, and apply polynomial operations to solve problems. Practice sorting gumballs with like terms and creating nu
0 views • 23 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Understanding the Extension Theorem in Polynomial Mathematics
Explore the proof of the Extension Theorem, specializing in resultant calculations of polynomials and their extensions. Learn about Sylvester matrices, resultants, and how to make conjectures based on polynomial interactions. Take a deep dive into specializations and their implications in polynomial
0 views • 14 slides
Understanding Zeroes of Polynomials - Grade 9 Chapter 2
Zeroes of a polynomial are the values of the variable that make the polynomial equal to zero. This concept is explored in Grade 9 Chapter 2, where students learn how to find the zeroes of a polynomial by equating it to zero. Through examples like p(x) = x - 4, students understand how to determine th
0 views • 10 slides