Understanding Conditional Probability and Bayes Theorem
Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati
1 views • 5 slides
Understanding Boolean Algebra: Duality Theorem, De-Morgan's Law, and Don't Care Conditions
Boolean algebra concepts such as the Duality Theorem, De-Morgan's Law, and Don't Care Conditions are essential for digital circuit design. The Duality Theorem states the relationship between a Boolean function and its dual function by interchanging AND with OR operators. De-Morgan's Law helps find t
0 views • 10 slides
Understanding Transmission Media and Twisted Pair Cables in Communication
Transmission media plays a crucial role in communication by transmitting data through electromagnetic signals. It is classified as guided media (using cables) and unguided media (waves through air, water, or vacuum). Twisted pair cables are a common type of guided media, consisting of insulated cond
5 views • 32 slides
Understanding Linear Discrimination for Classification
Linear discrimination is a method for classifying data where examples from one class are separable from others. It involves using linear models or high-order functions like quadratic to map inputs to class separable spaces. This approach can be further categorized as class-based or boundary-based, e
3 views • 37 slides
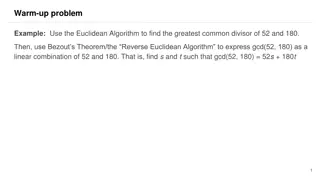
Understanding Linear Congruences and the Euclidean Algorithm in Number Theory
Exploring concepts of linear congruences using examples like finding times congruent to 2 o'clock and applying the Euclidean Algorithm to determine the greatest common divisor of 52 and 180. Learn about Bezout's Theorem for expressing GCD as a linear combination of the given numbers.
0 views • 26 slides
Understanding Linear Reservoir Baseflow Method
The linear reservoir baseflow method utilizes linear reservoirs to simulate the movement of water infiltrated into the soil. This method models water movement from the land surface to the stream network by integrating a linear relationship between storage and discharge. Users can select from one, tw
0 views • 11 slides
Understanding Linear Transformations and Matrices in Mathematics
Linear transformations play a crucial role in the study of vector spaces and matrices. They involve mapping vectors from one space to another while maintaining certain properties. This summary covers the introduction to linear transformations, the kernel and range of a transformation, matrices for l
0 views • 85 slides
Understanding the Coase Theorem: Property Rights and Economic Efficiency
The Coase Theorem, developed by economist Ronald Coase, posits that under certain conditions, bargaining related to property rights will lead to an optimal outcome regardless of the initial distribution. It provides a framework for resolving conflicts by emphasizing negotiation and efficient market
0 views • 10 slides
Understanding the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus states that if a function is continuous on an interval and has an antiderivative on that interval, then the integral of the function over the interval is equal to the difference of the antiderivative evaluated at the endpoints. This concept is further explored thr
0 views • 14 slides
Understanding Linear Programming: An Introduction to Optimization
Linear programming, introduced by mathematician George B. Dantzig in 1947, is a mathematical technique for optimizing resource allocation in a systematic manner. It involves formulating linear relationships among variables to achieve desired results like cost minimization or profit maximization. Lin
1 views • 60 slides
Understanding Myhill-Nerode Theorem in Automata Theory
Myhill-Nerode theorem states that three statements are equivalent regarding the properties of a regular language: 1) L is the union of some equivalence classes of a right-invariant equivalence relation of finite index, 2) Equivalence relation RL is defined in a specific way, and 3) RL has finite ind
1 views • 20 slides
Understanding the Pythagorean Theorem and Right-Angled Triangles
Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th
1 views • 25 slides
Engineering Mechanics: Lami's Theorem and Cylinder Reactions Problem
This course material covers Lami's Theorem in Engineering Mechanics taught by Ranbir Mukhya. It includes an outline of the theorem, problem scenarios involving cylinders with given weights and diameters, and the determination of reactions at various points. Detailed force diagrams and calculations a
0 views • 8 slides
Insights into the Mean Value Theorem and Its Applications
Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista
0 views • 14 slides
Understanding Ion-Pair Chromatography (IPC): Theory and Applications
Ion-Pair Chromatography (IPC) involves adding ionic surfactants to a reversed-phase Chromatography system to affect retention and selectivity of ionic compounds. Developed by Dr. Gordon Schill, IPC is crucial for resolving hydrophilic samples and controlling selectivity in separations. The theory in
7 views • 18 slides
Understanding the Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
0 views • 31 slides
Comprehensive Overview of Numerical Linear Algebra Methods for Solving Linear Systems
Explore numerical linear algebra techniques for solving linear systems of equations, including direct and iterative methods. Delve into topics like Gaussian elimination, LU factorization, band solvers, sparse solvers, iterative techniques, and more. Gain insights into basic iterative methods, error
6 views • 12 slides
Closest Pair and Convex Hull: Brute Force Approach
Closest Pair Problem in 2D involves finding the two closest points in a set by computing the distance between every pair of distinct points. The Convex Hull Problem determines the smallest convex polygon covering a set of points. Dr. Sasmita Kumari Nayak explains these concepts using a brute-force a
0 views • 15 slides
Understanding Superposition Theorem in Electrical Circuits
Superposition theorem in electrical circuits states that the effects of multiple voltage and current sources in a network can be analyzed independently and then combined algebraically. This allows for calculating the voltage and current distribution in a network more efficiently. The theorem involve
0 views • 9 slides
Understanding Lami's Theorem in Physics
Lami's Theorem is an equation that explains how the magnitudes of forces acting on a point keep an object in equilibrium. This theorem relates the forces with corresponding angles and is derived by understanding the sum of forces acting on a point. By utilizing complementary angles and the sine rule
0 views • 8 slides
Exploring the Pythagorean Theorem and Its Origins
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines
0 views • 21 slides
Understanding Multiple Right-Hand Sides in Linear Algebra
Exploring the concept of Multiple Right-Hand Sides (MRHS) in linear algebra, we delve into normal linear operations, algebraic attack conversions, and known plaintext-ciphertext pair attacks. Discover the significance of MRHS and its applications in solving systems of polynomial equations.
0 views • 18 slides
Understanding Linear Dependent and Independent Vectors
In linear algebra, when exploring systems of linear equations and vector sets, it is crucial to distinguish between linear dependent and independent vectors. Linear dependence occurs when one vector can be expressed as a combination of others, leading to various solutions or lack thereof in the give
0 views • 20 slides
Understanding Bayes Theorem in NLP: Examples and Applications
Introduction to Bayes Theorem in Natural Language Processing (NLP) with detailed examples and applications. Explains how Bayes Theorem is used to calculate probabilities in diagnostic tests and to analyze various scenarios such as disease prediction and feature identification. Covers the concept of
0 views • 13 slides
Understanding Linear Combinations and Common Divisors Theorem
Exploring the relationship between linear combinations and common divisors through the theorem connecting the greatest common divisor (GCD) and the smallest positive integer linear combination (SPC) of two integers a and b. The theorem states that the GCD is less than or equal to the SPC, with proof
0 views • 45 slides
Understanding Triangle Classification: Sides and Angles
Explore how to classify triangles based on their sides and angles, using the Triangle Sum Theorem and linear pair theorem to find missing angle measures. Learn to distinguish between different types of triangles such as right, isosceles, equilateral, and obtuse, and solve problems involving properti
0 views • 13 slides
Problem Solving with Pythagoras Theorem in Geometry
Explore the application of Pythagoras Theorem in solving problems related to right-angled triangles, diagonals of shapes like rectangles and rhombuses, and the height of triangles. Learn how to use Pythagoras Theorem effectively by drawing diagrams, identifying known lengths, and using the theorem t
0 views • 8 slides
Converting Left Linear Grammar to Right Linear Grammar
Learn about linear grammars, left linear grammars, and right linear grammars. Discover why left linear grammars are considered complex and how right linear grammars offer a simpler solution. Explore the process of converting a left linear grammar to a right linear grammar using a specific algorithm.
0 views • 44 slides
Understanding Linear Optimization in MS&E 214
Linear optimization involves maximizing or minimizing a linear function subject to constraints. This week's focus in MS&E 214 is on linear programming, basic feasible solutions, duality theory, and extreme point solutions. The concept of linear programs, such as the example of maximizing x + 3y subj
0 views • 36 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding Rolle's Theorem and The Mean Value Theorem in Calculus
Rolle's Theorem states that for a continuous and differentiable function on a closed interval with equal function values at the endpoints, there exists at least one point where the derivative is zero. The Mean Value Theorem asserts that for a continuous and differentiable function on an interval, th
0 views • 5 slides
Introduction to Analysis: Mean Value Theorem and Related Theorems
This resource delves into key concepts such as the Mean Value Theorem, Fermat's Theorem, Rolle's Theorem, Extreme Value Theorem, local maximums, and more. It presents important results and explores proofs in the context of analysis.
0 views • 71 slides
Adapting Linear Hashing for Flash Memory Constrained Embedded Devices
This research explores the adaptation of linear hashing for improved data handling on flash memory-constrained embedded devices. Motivated by the increasing data collection by IoT devices, the study focuses on implementing database structures like a linear hash table for efficient data processing. T
0 views • 67 slides
Introduction to Applying Pythagorean Theorem in Right Triangles
In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,
0 views • 13 slides
Understanding Linear Functions in Mathematics
Linear functions play a crucial role in mathematics, focusing on elements like rate of change and initial value. Through examples involving daily car rental costs and profit from selling birdhouses, this content explores the concept of linear functions and how they are applied in real-life scenarios
0 views • 13 slides
Understanding Binomial Theorem: Expansion, Examples, and Applications
Binomial theorem is a powerful mathematical concept used to expand expressions involving binomials. This presentation explores the basics of binomial expansion, formulae for positive, negative, and fractional indices, along with examples demonstrating its application. By leveraging the binomial theo
0 views • 10 slides
Understanding Automated Theorem Proving in Lean
Dive into the world of automated theorem proving in Lean with a focus on formal verification, history, and the use of logic and computational methods. Explore how programs can assist in finding and verifying proofs, as well as the significance of interactive theorem provers. Discover the evolution o
0 views • 35 slides
Understanding Linear and Nonlinear Functions in Mathematics
Explore the concepts of linear and nonlinear functions in mathematics through identifying linear and nonlinear functions from graphs, understanding the characteristics of linear functions, and identifying linear functions from tables. Learn about the constant rate of change, slope, and how to determ
0 views • 49 slides
Understanding Linear Error Control Coding and Syndrome Detection in Binary Linear Codes
Delve into the world of linear error control coding, guided by Prof. Janos Levendovszky, as we explore the development of linear codes, message vectors, error groups, and the process of selecting group leaders with detailed examples. Discover how syndrome detection and decoding tables play a crucial
0 views • 27 slides
Triangles Inequalities and The Hinge Theorem
Understanding the inequalities in triangles using the Hinge Theorem. The theorem explains how the length of the third side of a triangle relates to the included angles and congruent sides in different triangle configurations. Explore problems that involve applying the Hinge Theorem and its converse
0 views • 8 slides