Integral Calculus: Two Major Approaches & Antiderivatives
In this chapter, we delve into the fundamental concepts of integral calculus, focusing on two major approaches to mathematically generate integrals and assigning physical meanings to them. We explore antiderivatives, differentiation, integration, and the process of taking integration as the inverse
9 views • 59 slides
Review of Definite Integrals using the Residue Theorem
Singular integrals involving logarithmic and non-integrable singularities are discussed, emphasizing integrability in the principal value sense. Cauchy Principal Value integrals and examples of their evaluations for singularities like 1/x are explored, highlighting the necessity of passing through t
2 views • 48 slides
Accumulation Problems and Definite Integrals in Applied Calculus
Explore the interpretation of definite integrals in accumulation problems, where rates of change are accumulated over time. Learn how to solve accumulation problems using definite integrals and avoid common mistakes by understanding when to use initial conditions. Discover the relation between deriv
0 views • 9 slides
The Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
6 views • 31 slides
Integration: Geometrical Interpretation, Properties, and Methods
Integration is the inverse process of differentiation, where we find a function whose differential is given. This process involves basic formulae, methods like integration by parts, and geometrical interpretation. Properties of indefinite integrals and techniques such as integration by substitutions
8 views • 28 slides
Numerical Integration in Density Functional Theory (DFT)
The application of numerical integration techniques in Density Functional Theory (DFT) is crucial for solving the Eigenvalue Problem and evaluating energy functionals. This involves partitioning integrals, approximating integrals at atomic centers, defining partition functions, and ensuring cell fun
3 views • 15 slides
Geometric Probabilities: From Fractions to Integrals
Delve into the realm of geometric probabilities with insights on how to transition from fractions to definite integrals, utilizing technology for enhanced learning experiences. Understand the significance of probability calculations in quantifying likelihood, incorporating geometric representations
1 views • 26 slides
Coulomb Interaction in Many-Particle Hamiltonian
Explore the treatment of Coulomb interaction in a many-particle Hamiltonian, where careful integration is crucial due to divergence issues. Learn about solving the Coulomb Hamiltonian with Slater integrals and expanding the operator on spherical harmonics for analytical solutions. Discover the signi
2 views • 15 slides
Coulomb Repulsion and Slater Integrals
Dive into the intricate world of Coulomb repulsion and Slater integrals, essential concepts in quantum physics. Explore the challenges posed by the diverging Coulomb integral and the complex calculations required to evaluate these interactions. Discover how Slater integrals play a crucial role in cr
4 views • 14 slides
Applications of Definite Integrals in Finding Areas
Explore the practical applications of definite integrals through the concept of finding areas. These images illustrate how definite integrals are used to calculate areas bounded by curves and lines, offering a visual representation of the integral calculus in action.
1 views • 9 slides
Area, Riemann Sums, and Definite Integrals
Antiderivatives are utilized to find area under curves, where Riemann Sums are employed for approximations. The process involves dividing intervals into rectangles for both approximate and exact area calculations. Definite integrals provide specific, finite values representing total displacement, wi
0 views • 8 slides
Properties of Definite Integrals in Mathematics II Second Semester
Delve into the world of definite integrals in Mathematics II Second Semester, understanding rules, properties, and applications through examples. Learn to find bounds, evaluate integrals, calculate areas under curves, and graph functions for a comprehensive understanding of this mathematical concept
3 views • 15 slides
The Fundamental Theorem of Calculus
Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin
2 views • 15 slides
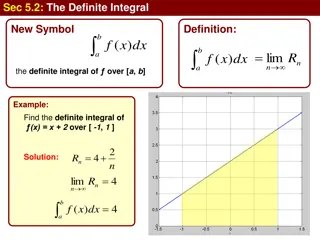
Definite Integrals in Calculus
Explore the concept of definite integrals in calculus, including their new symbol definition, area interpretation, and examples of evaluating integrals in terms of areas. Learn about the limits of integration, the procedure of integration, and how definite integrals can represent areas under curves.
4 views • 34 slides
Definite Integrals Using Graphing Display Calculator for Evaluation
Learn how to use a Graphing Display Calculator (GDC) to evaluate definite integrals step-by-step. Follow the instructions provided in the images to input the function and calculate the result with the GDC. This interactive process helps in understanding how technology can assist in mathematical comp
1 views • 17 slides
Definite Integrals in Mathematics
Explore the concept of definite integrals in mathematics, covering properties, solving methods, and applications in finding areas bounded by curves. Prior knowledge of functions, limits, derivatives, and indefinite integrals is essential to grasp this topic effectively. Dive into the unique value of
1 views • 32 slides
Integration and Antiderivatives
Exploring the concepts of definite and indefinite integrals, Riemann sums, and antiderivatives in calculus. Learn about interpreting the definite integral, Riemann sums as rectangles approximating integrals, and finding general antiderivatives. Discover various formulas for finding antiderivatives o
4 views • 16 slides
Analytical Integration of Functions: A Comprehensive Guide
Functions and their integrals are explored in this guide, covering definitions, simple integration cases, examples, and well-known integrals. Learn about differential equations, inspection integration, and trigonometric functions. Master the techniques with detailed explanations and examples.
5 views • 20 slides
Methods of Integration and Trigonometric Substitution
Explore methods of integration including integration by parts and trigonometric substitution. Learn how to apply these techniques to solve integrals involving logarithmic, trigonometric, and rational functions. Discover step-by-step processes and identities to simplify and evaluate various types of
6 views • 7 slides
An Lp Theory for Outer Measures and Applications to Singular Integrals II
This content delves into the theory of outer measures, focusing on its application to singular integrals. It covers topics such as Carleson boxes, outer measures on the upper half-plane, sizes of functions on tents, outer essential supremum spaces, Lp spaces, embedding theorems, and weak L1-Sinfty e
2 views • 34 slides
Asymptotic Evaluation Techniques in Integral Calculus
Learn about asymptotic evaluation of integrals through techniques like integration by parts and the stationary-phase method. Understand how to handle integrals involving real functions, and grasp the significance of concepts like the Riemann-Lebesgue lemma and small o notation. Delve into the physic
3 views • 21 slides
Advanced Quantum Chemistry: Solving Secular Determinants and Integrals
Lecture 3 delves into secular determinants, overlap, resonance, and Coulomb integrals, introducing the Hückel approximation method for molecular orbital calculations in inorganic and solid-state chemistry. The lecture explains the approximations made, simplifying the calculation of integrals and en
1 views • 20 slides
Integration in the Complex Plane: Definitions and Equivalences
Learn about line integrals in the complex plane, equivalence between complex and real line integrals, and review of line integral evaluation. Understand how to evaluate line integrals using parameterization and examples.
1 views • 53 slides
Monte Carlo Integration in Computer Graphics: Overview and Applications
Explore Monte Carlo Integration in computer graphics, from motivation to algorithms, advantages, and disadvantages. Learn about its application in rendering complex shading effects and how it provides robust solutions for irregular domains and high-dimensional integrals. Understand the basics of pro
0 views • 51 slides
Matrix Models and Superintegrability: Deformations and Integrals
Explore the concepts of superintegrability, W-operators, and matrix integrals in mathematical physics through deformations and generalizations. Learn about matrix models, Hermitian Gaussian model, W-representations, and more. Discover the significance of deformation of integration space, combining W
3 views • 11 slides
Tutorial for Multiloop Calculations: Master Integrals & Automated Solutions
Learn about multiloop calculations in theoretical physics with a tutorial by Marvin Schnubel. Discover the step-by-step process of reducing to master integrals, creating diagrams, IBP reduction, and solving integrals with automated tools. Find out how to generate expressions and handle complex compu
2 views • 9 slides
Study of Scalar Box Diagram via Loop-Tree Duality Theorem
Explore the analysis of the scalar box diagram using the Loop-Tree Duality theorem to understand the origins of singularities. The work delves into N-particle scalar one-loop integrals, massless scalar box integrals, dual representations, and parametrization of momenta to compute integrals efficient
4 views • 14 slides
Reducing Feynman Integrals Using Blade in Collider Physics Workshop
Exploring the reduction of Feynman integrals using advanced techniques like Blade in the context of collider physics. This presentation covers perturbative calculations, IBP reduction, algorithms, examples, and the significance of reducing integrals for precise predictions in high-energy physics.
0 views • 29 slides
Fundamental Theorem of Calculus Part 2: Evaluation Theorem Explained
The Fundamental Theorem of Calculus, Part 2, also known as the Evaluation Theorem, allows us to evaluate definite integrals by finding antiderivatives. This theorem connects differential calculus and definite integrals, providing a powerful tool in calculus. Learn how to apply this fundamental conce
4 views • 10 slides
Advanced Techniques in Loop Corrections and Integral Reduction
Explore cutting-edge algorithms and methodologies for computing loop corrections, dimensional regularization, graph generation, integral reduction, and more in high-energy physics calculations. Learn about integration-by-parts identities, reduction of loop integrals to master integrals, and advanced
1 views • 21 slides
Proving Theorems on Definite Integrals at SGGSJ Government College, Paonta Sahib
Explore mathematical theorems on definite integrals at SGGSJ Government College, Paonta Sahib, with detailed proofs and explanations. Understand concepts such as definite integral properties and their applications in solving mathematical problems.
2 views • 12 slides
Engineering Mathematics: Application of Derivatives and Integrals
Explore the application of derivatives and antiderivatives in engineering mathematics. Learn about indefinite integrals, areas, distances, and more with examples and explanations provided by Asst. Lecturer Wisam Hayder at Diyala University College of Engineering.
0 views • 31 slides
Definite Integrals in Mathematics
Explore the concept of definite integrals in mathematics, including properties, solving methods, and application in finding areas bounded by curves. Prior knowledge in functions, limits, derivatives, and continuous functions is essential for understanding definite integrals.
2 views • 32 slides
Understanding Surface Integrals in Vector Fields
Learn about vector surface integrals in the context of electric flux, including how to calculate flux passing through a surface, quantify electric flux, and handle non-uniform electric fields and non-flat surfaces. Explore the concept through a series of informative slides.
4 views • 23 slides
Understanding Double Integrals in Mathematics
Learn about double integrals, their application in calculating volumes of three-dimensional solids, and how they are used to evaluate regions in the xy-plane. Explore exercises and definitions related to double integrals, along with Fubini's theorem and the concept of iterated integrals.
0 views • 6 slides
Integral Antiderivatives and Properties Overview
Understand the fundamental theorems, standard integrals, and properties of antiderivatives. Explore how integrals can define new functions and learn about the differentiation of functions defined by integrals.
2 views • 4 slides
Definite Integrals: Understanding Calculations and Applications in Mathematics
Explore the concept of definite integrals through topics like pre-requisite knowledge, area calculations, definite integral of a function, and applications in mathematics. Gain insights into the fundamentals of integrals and their practical uses in various scenarios.
0 views • 14 slides
Python Core Data Types Overview: Primitives, Integrals, and Floats
Explore Python's core data types including primitives, integrals (int, bool, float, complex), and floats. Learn about how these types are stored as objects, limitations, and special values. Understand the differences between integers versus floating-point numbers in Python.
2 views • 18 slides
Understanding Definite Integrals and Their Properties
Explore the concept of definite integrals, rules satisfied by them, and examples of evaluating integrals. Learn about the symbol notation, theorem related to antiderivatives, and properties such as zero width interval, constant multiple, sum, difference, and additivity. Practice solving integral pro
1 views • 13 slides
Understanding Multiple Integrals for T.Y.B.Sc. Students
Explore the concepts of multiple integrals in this chapter, extending from definite integrals to double and triple integrals of functions in two or three variables. Learn about volumes, masses of regions, using polar coordinates, and coordinate systems in three-dimensional space for simplifying trip
1 views • 36 slides