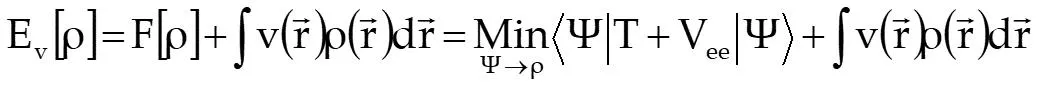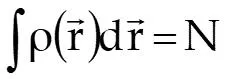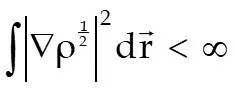Numerical Integration in Density Functional Theory (DFT)

The application of numerical integration techniques in Density Functional Theory (DFT) is crucial for solving the Eigenvalue Problem and evaluating energy functionals. This involves partitioning integrals, approximating integrals at atomic centers, defining partition functions, and ensuring cell functions meet specific conditions for accurate calculations in DFT.

• Numerical Integration
• Density Functional Theory
• DFT
• Energy Functionals
• Atomic Centers

caitlynru Follow

Uploaded on Sep 06, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Numerical Integration in DFT Patrick Tamukong The Kilina Group Chemistry & Biochemistry, NDSU

2. The Eigenvalue Problem in DFT In DFT, we seek = E Min E 0 v N where the energy functional is F ( ) ( ) r ( ) ( ) r r = + = + + E v r d r Min T V v r d v ee and the electron density is subject to the constraints ( ) r ( ) r 2 1 = 0 d r N d r 2 Due to the analytical complexity of exchange and correlation energy formulas, integrations are performed numerically 2

3. Partitioning of the Integral Express the integral as a sum over atomic centers = I A I A Function to be integrated ( ) ( F ) r d ( ) r F ( ) ( ) F r where A A A = = = = + + I I r d w r r d w r R r R A A A A A A A A Partition or weight function The partition or weight function fulfills the conditions ( ) r ( ) 1 r = 3 wA 0 w R r for any A A 3

4. Integral at Atomic Center Each integral at atomic centers is approximated as a sum of shell integrals over a series of concentric spheres centered at the nucleus of the atom ( ) A r A = 2 I 4 F r r d A A A 0 1 where ( ) A r ( ( ) s ) = F f r d s ( ) A A A = d s sin d d 4 A A A A A r Surface element in spherical coordinates integration over shell of radius The function to be integrated is ( ) ( ) ( ( ) s ) ( ) s ( ) s = + + f r w R r F R r 4 A A A A A A A

5. The Partition Function The partition function or nuclear weight at a given point is ( ) ( ) r p B ( ) ( ) ( ) A B function of atom A, composed of independent pair contributions ( ) r AB = ( ) r ( ) ( ) r p p r = = w r A A A z B is the unnormalized cell = p r s r where A AB ( ( ) r ) s AB The are hyperbolic coordinates defined as r r R r R r r ( ) A B = A R B AB R AB AB ( ) R ( ) 1 R B ( ) r 3 = R 1 r = 1 5 AB AB A AB

6. The Cell Function It must be close to unity near nucleus A and close to zero near other nuclei, thus the contribution between atoms A and B, , decreases monotonically as follows is subject to the conditions ( ) ( ) r s AB ( ) 1 ds ( ) ( ) 1 1 = = ds s 0 0 s 1 1 s 0 = 0 d d = 1 Gr fenstein, J.; Cremer, D. J. Chem. Phys.2007, 127, 164113. 6

7. Beckes Definition of The Cell Function According to Becke 1 1 ( ) ( ) = s p k 2 ( ) pk Where the polynormials are such that ( ) ( ) 3 1 = ( ) p p p = 3 p + k 1 k 1 2 2 Becke found k = 3 to be the optimum value for a sufficiently well-behaved . Since , it follows that ( ) p 1 2 ( ) - ( ) ( ( ) r ) = p p s AB 3 3 1 ( ) ( ) = + = s 1 s 3 Becke, A. D. J. Chem. Phys.1988, 88, 2547. 7

8. Properties of the Hyperbolic Coordinates Consider r r ( ) r = 1 1 A B AB R AB ( ( ) ) 2 = = + 2 B 2 A r r R r R R 2r cos Using the cosine rule A AB AB AB A A ( )( 2r ) ( ( ) ) + = r r r r R 2r cos R A B A B R AB A A AB ( ) r r r 2r cos R ( ) r = = A R B A A AB A r AB AB + + r r AB A B A B Tamukong, P. K. Extension andApplications of GVVPT2 to the Study of Transition Metals. Ph.D. Dissertation, University of North Dakota, Grand Forks, ND, 2014 (http://gradworks.umi.com/36/40/3640951.html). 8

9. Properties of the Hyperbolic Coordinates ( ) 0 r AB 1 Thus only within a sphere of radius r R A AB 2 ( ) r 1 iff that is 0 AB r R R A AB 2 At a fixed radius of a given sphere around atom A, and are even functions of the angle ( ) r AB B r A r A ( ) r r r 2r cos R 2r R From ( ) r = = A R B A A AB A r AB AB + + r r AB A B A B dr r R ( ) d 2r + 2 d r r R ( ) 2 ( ) d 2r + = sin B A AB ( ) = sin AB A = cos B A AB = cos AB A A A d r A d r r 2 A A d r 2 A d r r A B A A B B A B Tamukong, P. K. Extension andApplications of GVVPT2 to the Study of Transition Metals. Ph.D. Dissertation, University of North Dakota, Grand Forks, ND, 2014 (http://gradworks.umi.com/36/40/3640951.html). 9

10. Properties of the Hyperbolic Coordinates ( ) A 0 B r A= Thus has its maximum at and minimum at ( ) A AB A= Meanwhile has its maximum on the sphere 1 A= when s r R 0 A= and minimum when A A AB 2 10

11. Alternative Definition of Cell Function Stratmann et al. alternatively define the cell function as ( ) ( ) g 1 2 ( ) ga = 1 1 = s a Where is a piece-wise odd function defined as a, 1 a ( ) ( ) + ( ) 0 a 1 g z a a a a 3 5 7 1 ( ) = + z 35 35 21 5 a 16 a a a a Stratmann, R. E.; Scuseria, G. E.; Frisch, M. J. Chem. Phys. Lett. 1996, 257, 213. 11

12. Alternative Definition of Cell Function ( a a, ( ) ) za Within the limits , the function is subject to the constraints ( z z a a d ( ) za a = ( ) 1 a ( ) ) ( ) dz dza = = za a 1 za = = 0 a 0 d = a The function has zero second and third order derivatives at and leads to 1 ds 35 ( ) 0 = = s 2 d 32a = 0 The Stratmann et al. cell function satisfies 35 1 if a ( ) = = a 0.64814814 8 = s reliably 2 27 0 if a from the requirement that the derivatives of the Becke and Stratmann cell functions coincide at = 0 12

13. Selection of Significant Functions In performing integrations, advantage is taken of the fast decaying nature of Gaussian atomic orbitals such that for each grid point, only such functions that are numerically significant (according to a user-specified criterion, ) are considered ( ) i A gr gs A For grid point , a set of significant functions is chosen which satisfies ( ) A s A r R g g A radius of considered sphere 13

14. Selection of Significant Functions To maximize computational efficiency, blocks of grid points are used, e.g., a sphere of grid points with a set of significant basis functions g = G gr = g S s G g G ( ) A rg S G if A for some r R G g A ( ) r A L ( ) G Ar A ( ) r A L ( ) G Ar A 14

15. Thank You 15