Learn Past Continuous Tense - Grade 6 English Lesson
This Grade 6 English lesson focuses on understanding and correctly using the past continuous tense. It covers the rules for forming the past continuous tense, examples of its usage, and an assessment to test comprehension. Students will practice talking about actions happening at specific times in t
4 views • 6 slides
Discrete Math for Computer Science Course - ICS 6D, Spring 2016
Prof. Sandy Irani leads the ICS 6D Discrete Math for Computer Science course at UC Irvine. The course covers various topics in discrete mathematics, with lectures on Mondays, Wednesdays, and Fridays. Teaching assistants and readers support the course, which includes interactive activities on zyBook.
5 views • 32 slides
Understanding Interpolation and Pulse Shaping in Real-Time Digital Signal Processing
Discrete-to-continuous conversion, interpolation, pulse shaping techniques, and data conversion in real-time digital signal processing are discussed in this content. Topics include types of pulse shapes, sampling, continuous signal approximation, interpolation methods, and data conversion processes
4 views • 14 slides
Europe Continuous Bioprocessing Market
The Europe Continuous Bioprocessing Market is expected to grow at a CAGR of 19.1% from 2023 to 2030 to reach $206.1 million by 2030. Continuous manufacturing is an emerging trend spanning various industries. From automotive to paper, businesses are embracing continuous manufacturing to enhance effic
3 views • 2 slides
Discrete Mathematics
Explore the foundations of logic and proofs in discrete mathematics, focusing on compound propositions, bit operations, and applications of propositional logic. Learn about how computers use bits for information representation and manipulation, and delve into translating English sentences into logic
5 views • 15 slides
Understanding Types of Production Systems: Intermittent vs. Continuous
Types of production systems are categorized into Intermittent Production System and Continuous Production System. In Intermittent Production, goods are produced based on customer orders in a flexible and non-continuous manner, allowing for a variety of products. Examples include goldsmiths making or
10 views • 17 slides
Understanding Divisibility and Modular Arithmetic in Discrete Structures
This lecture discusses the concepts of divisibility and modular arithmetic in the context of discrete structures. It covers definitions, notation, and examples of divisibility by integers, including proving properties such as the divisibility of products and consecutive integers. Through practical e
1 views • 43 slides
Exploring Discretized Interpretation of Continuous Prompts
Delve into the analysis of discrete text prompts and their interpretation of continuous prompts in AI research. The work explores sentiment analysis using pre-trained language models along with recent breakthroughs in spatial reasoning. Discover the challenges in interpreting and optimizing text pro
0 views • 21 slides
Advancements in Discrete Auto Analyzers for Clinical Chemistry Operations
Discrete auto analyzers integrate specimen handling, reagent systems, optical components, and computers for streamlined functionality. The innovation in computer technology, particularly microprocessors, has revolutionized these analyzers, enabling precise data management, liquid handling, and optic
0 views • 17 slides
Microeconometric Modeling with Multinomial Logit Model
The topic discusses the Multinomial Logit Model in the context of discrete choice modeling, covering concepts, models, consumer preferences, utility maximization, and implications for discrete choice models. It explores how consumers maximize utility under budget constraints, the need for well-defin
1 views • 58 slides
Understanding Random Variables and Their Applications in Various Fields
Random variables play a crucial role in statistics, engineering, and business applications. They can be discrete or continuous, depending on the nature of the outcomes. Discrete random variables have countable values, while continuous random variables can take on any real number. This article explor
0 views • 6 slides
Understanding Discrete Optimization in Mathematical Modeling
Discrete Optimization is a field of applied mathematics that uses techniques from combinatorics, graph theory, linear programming, and algorithms to solve optimization problems over discrete structures. This involves creating mathematical models, defining objective functions, decision variables, and
0 views • 12 slides
Understanding Continuous Monitoring in Risk Management Framework (RMF)
Explore the continuous monitoring process in the Risk Management Framework (RMF) under the NISP RMF FISWG. Learn about the six steps in the RMF process, DSS-provided RMF guidance, and an overview of RMF continuous monitoring strategies and security control families. Discover how to outline DSS RMF p
1 views • 25 slides
Understanding Binomial and Poisson Data Analysis
Discrete data, including Binomial and Poisson data, plays a crucial role in statistical analysis. This content explores the nature of discrete data, the concepts of Binomial and Poisson data, assumptions for Binomial distribution, mean, standard deviation, examples, and considerations for charting a
2 views • 31 slides
Noise & Error Shaping in Discrete-Time DSMs EECT 7V88 - Fall 2021
Explore the intricacies of noise and error shaping in DSMs with Professor Y. Chiu's course on Discrete-Time DSMs for EECT 7V88 in Fall 2021. Delve into DAC architectures including Nyquist, binary-weighted, and more. Learn about Binary-Weighted CR DAC, CP Cu, capacitor arrays, gain errors, nonlineari
0 views • 30 slides
Understanding Logical Connectives in Discrete Mathematics
Explore the world of propositional logic and truth tables in discrete mathematics through a peer-instruction approach. Learn about basic logical connectives, new connectives, complex formulas, operator precedence, and the nuances of implication (implies) with engaging examples. Delve into scenarios
0 views • 14 slides
Understanding Boolean Logic and Contrapositive Forms in Discrete Math
Delve into the world of Boolean logic and contrapositive forms in discrete math through topics such as simplifications, DeMorgan's Laws, and conditional operators. Explore how to identify equivalent Boolean expressions and prove contrapositive statements using logical reasoning.
0 views • 22 slides
Understanding Sampling and Signal Processing Fundamentals
Sampling plays a crucial role in converting continuous-time signals into discrete-time signals for processing. This lecture covers periodic sampling, ideal sampling, Fourier transforms, Nyquist-Shannon sampling, and the processing of band-limited signals. It delves into the relationship between peri
1 views • 60 slides
Resolution in Discrete Math: Exercise on Rules of Inference
Using resolution in the context of discrete mathematics, this exercise demonstrates how the hypotheses related to rain, umbrellas, and getting wet are logically connected to show that Yvette does not get wet. The solution breaks down the assumptions and applies resolution to derive the final conclus
0 views • 4 slides
Understanding Direct Proofs in Discrete Mathematics
Explore the principles of direct proof in discrete mathematics through a Peer Instruction approach by Dr. Cynthia Bailey Lee and Dr. Shachar Lovett. Learn how to prove theorems of the form "if p, then q" using logical rules, algebra, and math laws. Utilize a clear template for direct proofs, practic
0 views • 17 slides
Guide to Direct Proofs in Discrete Math
Dive into the world of direct proofs in discrete math with this comprehensive guide. Learn how to prove implications, create truth tables, and follow a step-by-step direct proof template. Test your understanding with engaging quizzes and practical examples. Master the art of logical reasoning and fo
0 views • 18 slides
Oregon District Continuous Improvement Planning Process
Explore the key components of Oregon's district continuous improvement planning process, including objectives, executive memos, ODE commitments, and the essential elements that all Oregon districts must incorporate into their continuous improvement plans. Learn about the shifts in the overarching vi
0 views • 9 slides
Understanding Discrete Probability Distributions
Explore the definition of random variables, probability distributions, and three types of discrete distributions - Binomial, Hypergeometric, and Poisson. Learn about the mean, variance, and standard deviation of probability distributions, as well as the difference between discrete and continuous dis
3 views • 32 slides
Exploring Discrete Mathematics through Graph Theory
Delve into the world of discrete mathematics with a focus on graph theory. Learn about graphs, their properties, and essential theorems. Discover how graphs model relations in various applications like network routing, GPS guidance, and chemical reaction simulations. Explore graph terminology, theor
0 views • 26 slides
Understanding Combinatorics in Discrete Mathematics
Combinatorics, a key facet of discrete mathematics, explores the arrangement of objects and finds applications in various fields like discrete probability and algorithm analysis. The Rule of Sum, a fundamental principle, dictates how tasks can be accomplished when they cannot be done simultaneously.
0 views • 70 slides
Understanding Arithmetic Mean Calculation Methods
Arithmetic mean can be calculated in individual, discrete, and continuous series. In individual series, each item is listed separately, while in discrete and continuous series, items are grouped with frequencies. The mean can be computed using formulas tailored to each type of series, including meth
0 views • 4 slides
Understanding Laplace Transforms for Continuous Random Variables
The Laplace transform is introduced as a generating function for common continuous random variables, complementing the z-transform for discrete ones. By using the Laplace transform, complex evaluations become simplified, making it easy to analyze different types of transforms. The transform of a con
0 views • 17 slides
Introduction to Sequential Pattern Mining Overview
Discover the concept of sequential pattern mining, a popular data mining task introduced in 1994, with a focus on analyzing discrete sequences to find interesting patterns. Sequential pattern mining involves finding frequent subsequences in sets of discrete sequences, such as items purchased by cust
1 views • 24 slides
Understanding Valid and Invalid Arguments in Discrete Mathematics
Concepts of valid and invalid arguments in discrete mathematics are explored through examples. Learn how to determine the validity of arguments based on premises and conclusions. Practice using truth tables to evaluate argument forms. Enhance your logical reasoning skills in Discrete Mathematics.
0 views • 22 slides
Discrete Scenarios in Graphs
The scenarios where the height of a student depending on age, time taken in a race depending on distance, number of students taking a test depending on class size, and length of a walkway depending on number of bricks are analyzed to determine which would result in a discrete graph with isolated poi
1 views • 23 slides
Understanding Probability Density Functions for Continuous Random Variables
Probability density functions (PDFs) are introduced for continuous random variables to represent the likelihood of events in a continuous space. Unlike discrete probability mass functions, PDFs operate with integration instead of summation, ensuring total probability is 1. Consistency and differenti
1 views • 32 slides
Understanding Discrete Random Variables and Variance Relationships
Explore the concepts of independence in random variables, shifting variances, and facts about variance in the context of discrete random variables. Learn about key relationships such as Var(X + Y) = Var(X) + Var(Y) and discover common patterns in the Discrete Random Variable Zoo. Embrace the goal of
0 views • 27 slides
Overview of Different Types of Fermentation Processes
Explore the various types of fermentation processes including batch fermentation, fed-batch fermentation, continuous fermentation, solid-state fermentation, anaerobic fermentation, and aerobic fermentation. Each process has its own advantages and disadvantages, influencing factors such as sterilizat
0 views • 18 slides
Coexistence of Continuous Cross-Border Intraday Markets and Implicit Auctions
Intraday cross-border continuous markets combine continuous trading with optional intraday auctions, providing participants with opportunities to trade firm energy within price areas. The coexistence of continuous trading and implicit auctions offers advantages such as market price acquisitions and
0 views • 9 slides
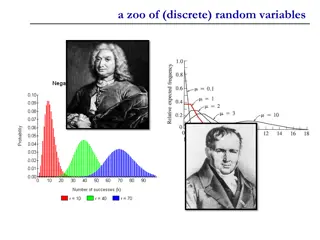
Understanding a Zoo of Discrete Random Variables
Discrete random variables play a crucial role in probability theory and statistics. This content explores three key types: Bernoulli random variable, binomial random variable, and error-correcting codes. From understanding the basics of Bernoulli trials to exploring the application of error correcti
0 views • 27 slides
Discrete Optimization Methods Overview
Discrete optimization methods, such as total enumeration and constraint relaxations, are valuable techniques for solving problems with discrete decision variables. Total enumeration involves exhaustively trying all possibilities to find optimal solutions, while constraint relaxations offer a more tr
0 views • 80 slides
Predicates and Quantifiers Exercise Solutions in Discrete Mathematics
Exercise solutions involving predicates and quantifiers related to printer status, job status, and queueing in a discrete mathematical context. The solutions address scenarios like lost jobs, busy printers, queued jobs, and out-of-service printers. References to textbooks in discrete mathematics are
0 views • 4 slides
Continuous Audit at Insurance Companies
Creating a rule-based model for anomaly detection, this research focuses on developing an architecture for continuous audit systems. By utilizing historical data, the scope includes detecting fraud, discrepancies, and internal control weaknesses, leading to a maturity model for automated continuous
0 views • 27 slides
Understanding Cyclic Groups and Discrete Logarithms
Exploring the concepts of cyclic groups and discrete logarithms in group theory. This presentation covers the definition of generators, examples of cyclic groups, important theorems related to prime orders and cyclic groups, uniform sampling in cyclic groups, and the discrete logarithm problem. Exam
0 views • 14 slides
Utilizing Present Continuous & Verb 'Can' in English Grammar Lessons
In this English grammar lesson, students learn to use the present continuous tense for activities happening at the moment or future plans. They also understand the usage of 'can' for expressing ability positively or negatively. The rules for forming present continuous verbs and examples are provided
0 views • 9 slides