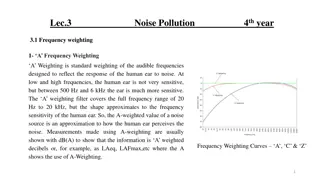
Noise & Error Shaping in Discrete-Time DSMs EECT 7V88 - Fall 2021
Explore the intricacies of noise and error shaping in DSMs with Professor Y. Chiu's course on Discrete-Time DSMs for EECT 7V88 in Fall 2021. Delve into DAC architectures including Nyquist, binary-weighted, and more. Learn about Binary-Weighted CR DAC, CP Cu, capacitor arrays, gain errors, nonlinearity, and more in this detailed study on DSMs. Discover the importance of stray-insensitive CR DACs, MSB transition codes, DNL errors, and code transitions to enhance your understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 DAC Architecture 1
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 DAC Architecture Nyquist DAC architectures Binary-weighted DAC Unit-element (thermometer-coded) DAC Segmented DAC Resistor-string, current-steering, charge-redistribution DACs Oversampling DAC Oversampling performed in digital domain (zero stuffing) Digital noise shaping ( modulator) 1-bit DAC can be used Analog reconstruction/smoothing filter 2
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Binary-Weighted DAC 3
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Binary-Weighted CR DAC CP Cu = unit capacitance Vo VX 8Cu 4Cu 2Cu Cu Cu VR b3 b2 b1 b0 Binary-weighted capacitor array most efficient architecture Bottom plate @ VR with bj = 1 and @ GND with bj = 0 4
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Binary-Weighted CR DAC CP Vo VX N = N j b 2 C N j u 8Cu 4Cu 2Cu Cu Cu j 1 = V V o R N = + + N j C C 2 C p u u j 1 VR N = N j b 2 C N j u b3 b2 b1 b0 j 1 = V R + N C 2 C p u b N 2 C N = j N j - = V V u o R + N j C 2 C 2 1 p u Cp gain error (nonlinearity if Cp is nonlinear) INL and DNL limited by capacitor array mismatch 5
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Stray-Insensitive CR DAC b N 2 C N = j N j - = V V u o R + + N 1 j C 2 C C 2 1 p u u + N 2 C 16Cu u A CP Vo VX A 8Cu 4Cu 2Cu Cu Large A needed to attenuate summing-node charge sharing VR b3 b2 b1 b0 6
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 MSB Transition Code 1000 Code 0111 + + j=1 C C C C ( ) ( ) = = V 0111 V V 1000 V 1 2 3 4 o R o R 4 4 j=1 C +C + C C +C + C p 0 j p 0 j ( ) + + = + Assume : C C C C C C, 4 1 2 3 u ( ) ( ) = DNL V 1000 V 0111 1LSB 1LSB o o C C = = C u C C u C Largest DNL error occurs at the midpoint where MSB transitions, determined by the mismatch between the MSB capacitor and the rest of the array. 7
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Midpoint DNL C < 0 C > 0 Ao Ao +DNL -DNL 0 0 Di Di 0111 1000 0111 1000 C > 0 results in positive DNL C < 0 results in negative DNL or even nonmonotonicity 8
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Output Glitches Cause: Signal and clock skew in circuits Especially severe at MSB transition where all bits are switching Vo 0111 111 Time 1000 000 Glitches cause waveform distortion, spurs and elevated noise floors High-speed DAC output is often followed by a de-glitching SHA 9
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 De-Glitching SHA b1 ... DAC SHA Vo bN SHA samples the output of the DAC after it settles and then hold it for T, removing the glitching energy. Vo Time SHA output must be smooth (exponential settling can be viewed as pulse shaping SHA BW does not have to be excessively large). 10
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Frequency Response |H(f)| SHA ZOH 0 f fs 2fs 3fs ( ) T 1 sin ( ) T = H j ( ) 2 j = H j e 2 SHA + 1 j ZOH T 2 3dB 11
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Binary-Weighted Current DAC b N = j N j - = R V IR o j 2 1 VX Vo b3 b2 b1 b0 A I/2 I/4 I/8 I/16 Current switching is simple and fast Vo depends on Rout of current sources without op-amp INL and DNL depend on matching, not inherently monotonic Large component spread (2N-1:1) 12
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 R-2R DAC b N = j N j - = V IR R o j 2 1 VX Vo b3 b2 b1 b0 A 2R 2R 2R 2R I/2 I/4 I/8 I/16 R R R 2R I A binary-weighted current DAC Component spread greatly reduced (2:1) 13
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Unit-Element DAC 14
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Resistor-String DAC Di VR b0 b0 b1 b1 3 2 1 Vo 0 Vo Simple, inherently monotonic good DNL performance Complexity speed for large N, typically N 8 bits 15
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Code-Dependent Ro VR Di b0 b0 b1 b1 Vo Vo Co t Signal-dependent RoCo causes HD Ro Ro of ladder varies with signal (code) On-resistance of switches depend on tap voltage 16
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 DNL R+ R1 R+ R2 R+ RN-1 R+ RN ... R= 0, VR R V1 V2 VN VN+1 j 1 j 1 j 2 ( ) ( ) + + R j 1 R j 2 R R R k k k = = = V V V V V 1 1 1 j R R j- 1 R N N N + + R NR NR R R k k k 1 1 1 + R R R NR V N j 1 j 1 = + V V V V R j j-1 R R N 1 V N + NR R k R V N R j 1 = = = DNL V V DNL 0, R R R j j j-1 DNL R 17
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 INL j 1 N j 1 j 1 ( ) ( ) ( ) + N j - 1 j 1 R R + R j 1 R R k k k k j 1 1 j = = + V V V V V 1 1 j R R R R N N 2 N N R + R NR R k k 1 1 ( )( ) + j 1 N- j 1 N N 2 j 1 = 2 2 V V , V R j R V R 3 2 R j 2 1 N 2 N 2 ( ) = + 1 2 2 max V , when j R V R 2 4N R j N 2 V N j-1 N R ( ) = = INL V V INL 0, max R R j j R INL 18
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 INL and DNL of BW DAC A BW DAC is typically constructed using unit elements, the same way as that of a UE DAC, for good component matching accuracy. N 2 R ( ) = INL 0, max R INL R ( ) = = 2 INL DNL 0, max N R DNL 19
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Current-Steering DAC Io I I I Binary-to-Thermometer Decoder b1 bN ... Fast, inherently monotonic good DNL performance Complexity increases for large N, requires B2T decoder 20
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Unit Current Cell Io ... bN Sj Sj ROW/COL Decoder ... b1 I 2N current cells typically decomposed into a (2N/2 2N/2) matrix Current source cascoded to improve accuracy (Ro effect) Coupled inverters improve synchronization of current switches 21
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Segmented DAC 22
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 BW vs. UE DACs Binary-weighted DAC Unit-element DAC Pros Min. # of switched elements Simple and fast Compact and efficient Pros Good DNL, small glitches Linear glitch energy Guaranteed monotonic Cons Large DNL and glitches Monotonicity not guaranteed Cons Needs B2T decoder Complex for N 8 INL/DNL INL(max) ( N/2) DNL(max) 2*INL INL/DNL INL(max) ( N/2) DNL(max) Combine BW and UE architectures Segmentation 23
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Segmented DAC VFS MSB DAC: M- bit UE DAC LSB DAC: L-bit BW DAC Resolution: N = M + L Vo MSB s 2M+L switching elements Good DNL Small glitches LSB s Same INL as BW or UE 0 2N-1 0 Di 24
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Comparison Example: N = 12, M = 8, L= 4, = 1% Architecture # of s.e. INL DNL Unit-element 2N = 4096 0.32 LSB s 0.01 LSB s Binary-weighted N = 12 0.32 LSB s 0.64 LSB s Segmented 2M+L = 260 0.32 LSB s 0.06 LSB s Max. DNL error occurs at the transitions of MSB segments 25
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Example: 8+2 Segmented Current DAC Ref: C.-H. Lin and K. Bult, A 10-b, 500-MSample/s CMOS DAC in 0.6mm2, IEEE Journal of Solid-State Circuits, vol. 33, pp. 1948-1958, issue 12, 1998. 26
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 MSB-DAC Biasing Scheme Common-centroid global biasing + divided 4 quadrants of current cells 27
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 MSB-DAC Biasing Scheme 28
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 Randomization and Dummies 29
Noise & Error Shaping in DSMs EECT 7V88 Discrete-Time DSM Professor Y. Chiu Fall 2021 References 1. M. J. M. Pelgrom, JSSC, pp. 1347-1352, issue 6, 1990. 2. D. K. Su and B. A. Wooley, JSSC, pp. 1224-1233, issue 12, 1993. 3. C.-H. Lin and K. Bult, JSSC, pp. 1948-1958, issue 12, 1998. 4. K. Khanoyan, F. Behbahani, A. A. Abidi, VLSI, 1999, pp. 73-76. 5. K. Falakshahi, C.-K. Yang, B. A. Wooley, JSSC, pp. 607-615, issue 5, 1999. 6. G. A. M. Van Der Plas et al., JSSC, pp. 1708-1718, issue 12, 1999. 7. A. R. Bugeja and B.-S. Song, JSSC, pp. 1719-1732, issue 12, 1999. 8. A. R. Bugeja and B.-S. Song, JSSC, pp. 1841-1852, issue 12, 2000. 9. A. van den Bosch et al., JSSC, pp. 315-324, issue 3, 2001. 30