Mathematics Course Selection Guide for Fall Semester
Academic advisors Olivia Biehle, Nathaniel Sulapas, and Jennifer McHam at the University of Texas provide guidance on selecting mathematics courses for the fall semester. The guide includes information on course sequences, considerations based on UTMA scores, AP credit recommendations, dual credit o
3 views • 20 slides
Understanding Dental Calculus Formation and Classification
Dental calculus, also known as tartar, is a mineralized bacterial plaque that forms on natural teeth and dental prostheses. It can be classified as supragingival or subgingival based on its relation to the gingival margin. This hard deposit is formed through the mineralization of dental plaque and c
5 views • 36 slides
AQA Level 2 Certificate in Further Maths
The AQA Level 2 Certificate in Further Maths is designed for high-achieving students to develop advanced skills in algebra, geometry, calculus, matrices, trigonometry, functions, and graphs. The course covers topics like number fractions, decimals, algebraic fractions, coordinate geometry, calculus,
7 views • 9 slides
Understanding Integral Calculus: Two Major Approaches & Antiderivatives
In this chapter, we delve into the fundamental concepts of integral calculus, focusing on two major approaches to mathematically generate integrals and assigning physical meanings to them. We explore antiderivatives, differentiation, integration, and the process of taking integration as the inverse
2 views • 59 slides
Understanding Numerical Methods for Approximating Analytic Equations
Introduction to approximating solutions to analytic equations, focusing on differential equations, integral equations, and integro-differential equations. Exploring ordinary and partial derivatives, differential and integral equations, and the involvement of unknown functions and their derivatives a
2 views • 15 slides
Understanding Related Rates and Differentials in Calculus
Derivatives involve very small changes in variables, leading to differentials. Related rates in calculus help us find how variables change in relation to each other. Learn how to solve related rates problems step by step with examples involving volumes, radii, and rates of change.
0 views • 11 slides
Understanding Classical Mechanics: Variational Principle and Applications
Classical Mechanics explores the Variational Principle in the calculus of variations, offering a method to determine maximum values of quantities dependent on functions. This principle, rooted in the wave function, aids in finding parameter values such as expectation values independently of the coor
0 views • 16 slides
Differential Equations of First Order & Higher Degree: Lecture 18
This lecture covers differential equations of first order but not of the first degree, general forms of such equations, methods for solving them, and examples of differential equations to be solved. The content includes detailed explanations, equations, solutions, and problem-solving techniques.
0 views • 9 slides
Understanding WBC Differential Count in Blood Analysis
WBC (white blood cell) count is essential in assessing a patient's health. A differential count helps determine the percentage of different types of white blood cells. This analysis can provide important insights into various health conditions like infections, allergies, and systemic illnesses. The
1 views • 9 slides
Understanding the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus states that if a function is continuous on an interval and has an antiderivative on that interval, then the integral of the function over the interval is equal to the difference of the antiderivative evaluated at the endpoints. This concept is further explored thr
0 views • 14 slides
Understanding Differential Leveling in Surveying
Differential leveling is a crucial aspect of surveying that involves determining the elevation of points with respect to a reference datum. This process includes various key elements such as benchmark, back sight, fore sight, and change points. By utilizing methods like the Height of Instrument and
1 views • 12 slides
Integrating Reverse Chain Rule and Substitution in Calculus
Explore the concepts of reverse chain rule and substitution in integration through worked examples and practice questions involving trigonometric functions. Enhance your skills with interactive narration and practical exercises. Dive into the world of calculus with a silent teacher guiding you throu
0 views • 5 slides
Understanding Points of Inflection in Calculus
Points of inflection in calculus refer to points where the curve changes from convex to concave or vice versa. These points are identified by observing changes in the curve's concavity, and they are not always stationary points. A stationary point can be a point of inflection, but not all points of
0 views • 14 slides
Understanding Accumulation Problems and Definite Integrals in Applied Calculus
Explore the interpretation of definite integrals in accumulation problems, where rates of change are accumulated over time. Learn how to solve accumulation problems using definite integrals and avoid common mistakes by understanding when to use initial conditions. Discover the relation between deriv
0 views • 9 slides
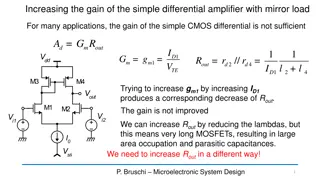
Techniques to Increase Gain in a Simple Differential Amplifier
Explore methods to boost the gain of a simple CMOS differential amplifier by replacing the current mirror with a cascode mirror, adding a common-gate stage, and employing a cascode differential amplifier. These techniques help improve Rout without extensive use of long MOSFETs, optimizing the amplif
2 views • 30 slides
Understanding Rates of Change and Calculus Concepts
Exploring the concept of rates of change through examples like finding the equation of a line passing through given points and understanding differentiation to calculate gradients and speeds. The relationship between gradients, curves, and tangents is highlighted to illustrate how calculus helps in
1 views • 21 slides
Calculus Examples and Practice
Explore various calculus problems involving finding gradients, equations of tangents and normals, and analyzing curves. Practice determining gradients at specific points, solving for coordinates, and differentiating equations to find tangent and normal lines. Understand the relationship between grad
1 views • 11 slides
Understanding Differential Equations: Types, Classification, and Solutions
Differential equations are mathematical equations that relate independent and dependent variables through differential coefficients. They can be classified as ordinary or partial, based on the types of derivatives involved. The order and degree of a differential equation, as well as its linearity an
3 views • 26 slides
Understanding Differential Equations in Economics Honours
Differential equations, introduced by Newton and Leibniz in the 17th century, play a key role in economics. These equations involve derivatives and represent implicit functional relationships between variables and their differentials, often related to time functions. The order and degree of a differ
1 views • 16 slides
Introduction to Differential Equations and Laplace Equations
Understanding differential equations of various orders, solving methods, linear and non-linear equations, ordinary and partial differential equations, definitions of solutions, and general vs. particular solutions in the context of Differential Equations and Laplace Equations.
1 views • 20 slides
Overview of Vector Calculus for ECE 3317 Course
This overview provides a brief explanation of vector calculus concepts essential for the ECE 3317 course on Applied Electromagnetic Waves. It covers del operator, gradient, divergence, curl, vector Laplacian, vector identities, and their applications in electromagnetic field theory.
0 views • 24 slides
Techniques of Integration in Calculus II
Explore various techniques of integration in Calculus II such as basic integration formulas, simplifying substitutions, completing the square, expanding powers with trigonometric identities, and eliminating square roots. Examples and solutions are provided to help understand these integration method
0 views • 8 slides
Understanding Formal Semantics of Programming Languages: From Lambda Calculus to Separation Logic
Explore the foundational concepts of formal semantics in programming languages, covering Lambda Calculus, Untyped and Simply-typed languages, Imperative languages, Operational and Hoare logics, as well as Separation logic. Delve into syntax, reduction rules, typing rules, and operational semantics i
7 views • 14 slides
Understanding Continuity and Differentiability in Calculus
This module covers the concepts of continuity and differentiability in calculus, including the definition of derivatives, differentiability criteria, the Chain Rule, and derivatives of implicit functions. The content discusses the relationship between continuity and differentiability, previous knowl
0 views • 12 slides
Understanding Differential Equations in Physical Phenomena
Differential equations play a crucial role in modeling physical phenomena involving rates of change like fluid motion, mechanical systems, and heat dissipation. This content explores examples of differential equations in motion and provides insights on sketching direction fields using tools like Map
0 views • 11 slides
Understanding Geometric Algebra and Calculus: A Deep Dive into Vector Derivatives and Maxwell Equations
Explore the world of geometric algebra and calculus through topics such as vector derivatives, Cauchy-Riemann equations, Maxwell equations, and spacetime physics. Unify diverse mathematical concepts to gain insights into analytic functions, differential operators, and directed integration.
0 views • 20 slides
Understanding Predicate Calculus: Symbols, Terms, and Variables
Predicate calculus extends propositional calculus by introducing symbols like truth values, constants, variables, and functions. It allows for precise manipulation of components within assertions, enabling the creation of general statements about classes of entities. Learn how predicates define rela
1 views • 14 slides
Exploring SymDiff: A Differential Program Verifier
SymDiff is a platform that leverages program verification to analyze program differences, focusing on differential verification to verify properties of program variances rather than the program itself. The architecture, language subset, and modeling imperative programs/heaps are key components discu
1 views • 18 slides
Understanding CMRR in Differential Amplifiers
Differential input amplifiers, including operational, instrumentation, and difference amplifiers, play a crucial role in amplifying differential signals while rejecting common-mode noise. The Common-Mode Rejection Ratio (CMRR) is a key parameter in these amplifiers, indicating their ability to suppr
0 views • 48 slides
Applications of Differential Equations in Engineering and Mathematics
Exploring the practical applications of differential equations, specifically focusing on Newton's Law of Cooling and Orthogonal Trajectories. The concept of exact differential equations and their solutions, along with real-life examples demonstrating temperature changes over time, are discussed. Und
0 views • 11 slides
Applications of Calculus in Optimization Problems
Calculus plays a crucial role in solving optimization problems to find maximum or minimum values in various real-life scenarios. This content provides examples of optimizing for maximum profit, area, distance, and volume using calculus concepts. From finding optimal dimensions for fencing to maximiz
0 views • 10 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding the Fundamental Theorem of Calculus
Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin
0 views • 15 slides
Understanding Differential Privacy in Statistical Analysis
Gain insight into the concept of differential privacy in statistical analysis through key terminologies, foundational ideas, and practical examples. Explore the balance between data privacy and statistical quality, and learn how differential privacy serves as a mathematical guarantee to protect indi
1 views • 28 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
Understanding Vector Calculus II Concepts with Examples by Prof. Somesh Kr. Malhotra
Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.
0 views • 29 slides
Solving Differential Equations: Methods and Techniques
Learn how to solve differential equations using methods like separation of variables and sketch families of solution curves. Understand the process of finding general and particular solutions to equations, and explore a variety of exercises and examples to enhance your understanding. Master the art
0 views • 16 slides
The Challenges of Protecting Privacy with Differential Privacy
The article discusses the motivation behind using differential privacy to protect sensitive data while enabling useful queries. It highlights the promise of differential privacy, challenges faced, attacks on existing systems like PINQ and Airavat, and introduces a defense system called The Fuzz. The
0 views • 24 slides
ME 130 Applied Engineering Analysis Class Fall 2018 at San Jose State University
San Jose State University's Department of Mechanical and Aerospace Engineering offers the ME 130 Applied Engineering Analysis course in Fall 2018 instructed by Dr. Tai-Ran Hsu. Prerequisite math courses include pre-calculus, calculus, and differential equations. Students are expected to have a solid
0 views • 14 slides
Introduction to Relational Calculus and Algebra in Database Management
Explore the fundamental concepts of relational calculus and algebra in the domain of database management. Understand the differences between declarative and imperative query languages and learn to retrieve information using practical examples and theoretical frameworks such as tuple relational calcu
0 views • 23 slides