Mathematics Course Selection Guide for Fall Semester
Academic advisors Olivia Biehle, Nathaniel Sulapas, and Jennifer McHam at the University of Texas provide guidance on selecting mathematics courses for the fall semester. The guide includes information on course sequences, considerations based on UTMA scores, AP credit recommendations, dual credit o
3 views • 20 slides
Understanding Dental Calculus Formation and Classification
Dental calculus, also known as tartar, is a mineralized bacterial plaque that forms on natural teeth and dental prostheses. It can be classified as supragingival or subgingival based on its relation to the gingival margin. This hard deposit is formed through the mineralization of dental plaque and c
5 views • 36 slides
AQA Level 2 Certificate in Further Maths
The AQA Level 2 Certificate in Further Maths is designed for high-achieving students to develop advanced skills in algebra, geometry, calculus, matrices, trigonometry, functions, and graphs. The course covers topics like number fractions, decimals, algebraic fractions, coordinate geometry, calculus,
7 views • 9 slides
Understanding Integral Calculus: Two Major Approaches & Antiderivatives
In this chapter, we delve into the fundamental concepts of integral calculus, focusing on two major approaches to mathematically generate integrals and assigning physical meanings to them. We explore antiderivatives, differentiation, integration, and the process of taking integration as the inverse
2 views • 59 slides
Understanding Related Rates and Differentials in Calculus
Derivatives involve very small changes in variables, leading to differentials. Related rates in calculus help us find how variables change in relation to each other. Learn how to solve related rates problems step by step with examples involving volumes, radii, and rates of change.
0 views • 11 slides
Calculus I Lecture #13: Volumes of Solids and Solids of Revolution
Exploring the concepts of finding volumes of solids using integrals, by slicing solid objects with parallel planes and calculating cross-sectional areas. Examples include calculating the volume of a pyramid and a curved wedge. The method of solids of revolution using the disk method is also discusse
0 views • 12 slides
Understanding Classical Mechanics: Variational Principle and Applications
Classical Mechanics explores the Variational Principle in the calculus of variations, offering a method to determine maximum values of quantities dependent on functions. This principle, rooted in the wave function, aids in finding parameter values such as expectation values independently of the coor
0 views • 16 slides
Understanding the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus states that if a function is continuous on an interval and has an antiderivative on that interval, then the integral of the function over the interval is equal to the difference of the antiderivative evaluated at the endpoints. This concept is further explored thr
0 views • 14 slides
Integrating Reverse Chain Rule and Substitution in Calculus
Explore the concepts of reverse chain rule and substitution in integration through worked examples and practice questions involving trigonometric functions. Enhance your skills with interactive narration and practical exercises. Dive into the world of calculus with a silent teacher guiding you throu
0 views • 5 slides
Understanding Points of Inflection in Calculus
Points of inflection in calculus refer to points where the curve changes from convex to concave or vice versa. These points are identified by observing changes in the curve's concavity, and they are not always stationary points. A stationary point can be a point of inflection, but not all points of
0 views • 14 slides
Understanding Accumulation Problems and Definite Integrals in Applied Calculus
Explore the interpretation of definite integrals in accumulation problems, where rates of change are accumulated over time. Learn how to solve accumulation problems using definite integrals and avoid common mistakes by understanding when to use initial conditions. Discover the relation between deriv
0 views • 9 slides
Understanding Rates of Change and Calculus Concepts
Exploring the concept of rates of change through examples like finding the equation of a line passing through given points and understanding differentiation to calculate gradients and speeds. The relationship between gradients, curves, and tangents is highlighted to illustrate how calculus helps in
1 views • 21 slides
Calculus Examples and Practice
Explore various calculus problems involving finding gradients, equations of tangents and normals, and analyzing curves. Practice determining gradients at specific points, solving for coordinates, and differentiating equations to find tangent and normal lines. Understand the relationship between grad
1 views • 11 slides
Insights into the Mean Value Theorem and Its Applications
Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista
0 views • 14 slides
Overview of Vector Calculus for ECE 3317 Course
This overview provides a brief explanation of vector calculus concepts essential for the ECE 3317 course on Applied Electromagnetic Waves. It covers del operator, gradient, divergence, curl, vector Laplacian, vector identities, and their applications in electromagnetic field theory.
0 views • 24 slides
Techniques of Integration in Calculus II
Explore various techniques of integration in Calculus II such as basic integration formulas, simplifying substitutions, completing the square, expanding powers with trigonometric identities, and eliminating square roots. Examples and solutions are provided to help understand these integration method
0 views • 8 slides
Understanding Formal Semantics of Programming Languages: From Lambda Calculus to Separation Logic
Explore the foundational concepts of formal semantics in programming languages, covering Lambda Calculus, Untyped and Simply-typed languages, Imperative languages, Operational and Hoare logics, as well as Separation logic. Delve into syntax, reduction rules, typing rules, and operational semantics i
7 views • 14 slides
Understanding Continuity and Differentiability in Calculus
This module covers the concepts of continuity and differentiability in calculus, including the definition of derivatives, differentiability criteria, the Chain Rule, and derivatives of implicit functions. The content discusses the relationship between continuity and differentiability, previous knowl
0 views • 12 slides
Understanding Geometric Algebra and Calculus: A Deep Dive into Vector Derivatives and Maxwell Equations
Explore the world of geometric algebra and calculus through topics such as vector derivatives, Cauchy-Riemann equations, Maxwell equations, and spacetime physics. Unify diverse mathematical concepts to gain insights into analytic functions, differential operators, and directed integration.
0 views • 20 slides
Understanding Rolle's Mean Value Theorem in Calculus
Rolle's Mean Value Theorem states that if a function is continuous in a closed interval, differentiable in the open interval, and the function values at the endpoints of the interval are equal, then there exists at least one point where the derivative of the function is zero. This theorem is verifie
0 views • 11 slides
Understanding Predicate Calculus: Symbols, Terms, and Variables
Predicate calculus extends propositional calculus by introducing symbols like truth values, constants, variables, and functions. It allows for precise manipulation of components within assertions, enabling the creation of general statements about classes of entities. Learn how predicates define rela
1 views • 14 slides
Linear Algebra and Vector Calculus Course Details
This course covers topics in linear algebra and vector calculus, including systems of linear equations, matrices, determinants, vector operations, functions of several variables, differentiation, and optimization. Textbooks by H. Anton and Swokowski are recommended, along with additional lecture not
0 views • 13 slides
Enhancing Math Pathways for College Completion
Addressing the significance of mathematics in degree completion, the Complete College Georgia initiative focuses on aligning gateway math courses with academic programs. Recommendations include offering Quantitative Reasoning and Introduction to Mathematical Modeling for non-STEM majors. The Algebra
0 views • 20 slides
Understanding Engineering Mathematics Fundamentals
Explore the core concepts of Algebra, Geometry, Trigonometry, and Calculus in engineering mathematics. Discover the historical roots, essential properties, and real-world applications of these mathematical principles, along with the significance of calculus for engineering students. Gain insights in
0 views • 41 slides
Calculus Derivatives and Rules
Explore the fundamental concepts of calculus involving product and quotient rules, derivatives of trigonometric functions, higher-order derivatives, and applications in position, velocity, and acceleration. The homework assignments provided further reinforce learning and mastery of these topics.
0 views • 8 slides
Isaac Newton: Contributions to Mathematics and Physics
Isaac Newton, a renowned physicist and mathematician from England, was the greatest scientist of his era. Despite being described as 'idle' and 'inattentive' in school, he formulated the Three Laws of Motion and the law of Universal Gravitation. Newton's mathematical contributions include studying p
0 views • 16 slides
Applications of Calculus in Optimization Problems
Calculus plays a crucial role in solving optimization problems to find maximum or minimum values in various real-life scenarios. This content provides examples of optimizing for maximum profit, area, distance, and volume using calculus concepts. From finding optimal dimensions for fencing to maximiz
0 views • 10 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding Analysis: Insights and Challenges in Advanced Mathematics
Dive into the world of advanced calculus and real analysis with insights from Dr. Wai W. Lau’s course at SPU. Explore the challenges and rewards of mastering calculus, the importance of multiple exposures to the subject, and the skills needed to excel in mathematical proofs. Gain valuable perspect
0 views • 31 slides
Understanding the Fundamental Theorem of Calculus
Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin
0 views • 15 slides
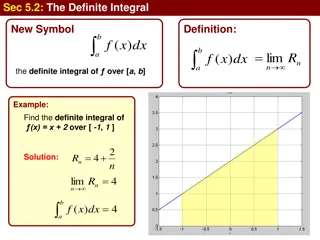
Understanding Definite Integrals in Calculus
Explore the concept of definite integrals in calculus, including their new symbol definition, area interpretation, and examples of evaluating integrals in terms of areas. Learn about the limits of integration, the procedure of integration, and how definite integrals can represent areas under curves.
0 views • 34 slides
Datalog Revival and Limitation of Relational Calculus
Datalog, a logic-based programming language, saw a revival in the 21st century with the addition of recursion to positive first-order queries. The history of Datalog traces back to the 1970s with the idea of adding recursion to FO queries. Despite the industry's initial lack of interest, Datalog fou
0 views • 45 slides
Enhancing Mathematical Understanding Through Collaborative Writing
Explore the intersection of creativity, mathematics, and education through initiatives like "Cocktail Party Calculus" where students engage in collaborative writing to enhance mathematical communication skills. Addressing the crisis of lack of understanding in mathematics, the importance of creativi
0 views • 27 slides
Understanding Related Rates Problems in Calculus
Calculus problems involving related rates often require identifying changing quantities, setting up equations, and using derivatives to find rates of change. Learn how to tackle scenarios like balloons, water tanks, inflating spheres, and pond ripples with step-by-step strategies and examples.
0 views • 11 slides
Understanding Vector Calculus II Concepts with Examples by Prof. Somesh Kr. Malhotra
Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.
0 views • 29 slides
Understanding Riemann Sums and Area Approximations in Calculus
Explore the concepts of Riemann sums, different types of approximations like left, right, and midpoint sums, trapezoidal rule, and interpreting area in real-life scenarios with examples. Learn how to apply these methods to approximate irregular areas and calculate distances and average speeds. Dive
0 views • 6 slides
Mastering Impact Calculus in Debate Rounds
Understand the importance of impacts in debate rounds, learn how to win by emphasizing impacts, compare economic suffering vs. illness during Covid-19, explore various impact comparisons like Economy vs. Environment, and grasp the significance of matters and comparisons in impacting. Practice your s
0 views • 18 slides
Understanding Dependent and Relative Motion in Dynamics
Dependent Motion and Relative Motion are fundamental concepts in Dynamics, providing the foundation for future analysis. Dependent Motion involves constraints like ropes or cables, while Relative Motion considers observers in motion. Dynamics involves applying a limited set of equations in diverse w
0 views • 18 slides
ME 130 Applied Engineering Analysis Class Fall 2018 at San Jose State University
San Jose State University's Department of Mechanical and Aerospace Engineering offers the ME 130 Applied Engineering Analysis course in Fall 2018 instructed by Dr. Tai-Ran Hsu. Prerequisite math courses include pre-calculus, calculus, and differential equations. Students are expected to have a solid
0 views • 14 slides
Understanding Related Rates in Calculus
Related rates problems in calculus involve finding the rate of change of one quantity with respect to another, utilizing concepts of implicit differentiation, chain rule, and relevant formulas. This includes scenarios such as ripples in a pond, inflating balloons, tracking airplanes, and filling tan
0 views • 9 slides