Understanding Related Rates Problems in Calculus
Calculus problems involving related rates often require identifying changing quantities, setting up equations, and using derivatives to find rates of change. Learn how to tackle scenarios like balloons, water tanks, inflating spheres, and pond ripples with step-by-step strategies and examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Related Rates 3.6
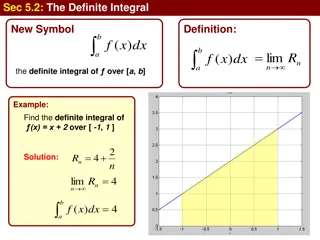
Rates of Change Since a derivative represents an instantaneous rate of change, we often see a rate of change represented as ?? ??or change in y with respect to time. y may represent distance (in which case ?? would be speed), Volume, Area, Profit, or any other unit which could be a function of time. We call ?? ??a time rate of change ??
Related Rates If you don t know the relationship between y and t (ie. y(t)) you can use the relationship between y and another variable x, IF we know ?? ??the rate of change in x with respect to time. We call ?? ??and ?? ??related rates
Run away balloon You are 150 feet away from a clown whose helium balloon that has come loose. If the balloon rises at a rate of 8 ft/sec, how fast is the distance between you an the balloon increasing when the balloon is 50 feet high?
General Strategy for Solving Related Rates Problems Step 1: Read the entire problem; identify quantities in the problem that are changing (moving). Choose clearly defined variable names for them. Draw a diagram; including labels. Step 2: Identify constants, values of functions, rates of change, and quantities that are functions of time. Identify which are given and which are to be found. Step 3: Find an equation that relates the variables whose rates of change are known to those variables whose rates of change are to be found. Step 4: Use implicit differentiation both sides of an equation with respect to time to relate the rates of the equation. Step 5: Substitute given constants, values of functions, and rates of change to solve for your rate to be found.
Water Tank Water is filling an open top conical tank at a rate of 2 cubic ft per minute. If the height of the tank is 16 feet and the radius of the opening is 4 feet, how fast is the water level rising when the water is 5 feet high? Cone Problem
Inflating Air is being pumped into a spherical balloon at a rate of 4.5 cubic feet per minute. Find the rate of change of the radius when the radius is 2 feet.
Pond Ripples A pebble is dropped into a calm pond causing ripples to form concentric circle . The radius of the outer ripple is increasing at a rate of 1 foot per second. When the radius is 4 feet, at what rate is the total area of the disturbed water changing?
Melting Ice Cream You are enjoying nice ice cream cone out in the cold which you decide to take with you into your friends car. Your friend is blasting the heat so your ice cream starts melting an drips out of the bottom of the cone at a rate of 20 cubic cm/min. Rather than trying to finish your ice cream or wiping up the mess, you decide to do some calculus instead because, hey, who wouldn t? If your cone has a height of 15 cm and base radius of 4 cm, how fast is the height of the melted ice cream dropping when the height of the melted ice cream is 5 cm?
Shuttle launch A camera tracks the launch of a spacecraft during a perfectly vertical launch. The camera is located on the ground 2 miles from the launch pad. If the rocket is 2.5 miles above ground and traveling at 700 mi/hr, at what rate is the camera angle (measured from the horizontal) changing? Give your answer in radians/s,
Hw Pg. 187 19, 23, 25, 27, 33, 35