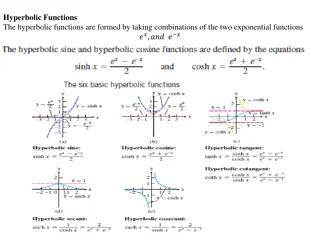
Understanding Set Theory: Infinite Sets and Functions
Delve into the world of discrete mathematics with a focus on set theory, particularly exploring infinite sets and functions. Learn about the concepts of countably infinite and uncountable sets, set equality based on bijective functions, and the properties of injective and surjective functions. Engage in mapping exercises from natural numbers to sets of positive evens and odds, grasping the essence of size and bijection in the realm of mathematics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Creative Commons License CSE 20 Discrete Mathematics Dr. Cynthia Bailey Lee Dr. Shachar Lovett Peer Instruction in Discrete Mathematics by Cynthia Leeis licensed under a Creative Commons Attribution- NonCommercial-ShareAlike 4.0 International License. Based on a work at http://peerinstruction4cs.org. Permissions beyond the scope of this license may be available at http://peerinstruction4cs.org.
2 Today s Topics: 1. Countably infinitely large sets 2. Uncountable sets To infinity, and beyond! (really, we re going to go beyond infinity)
3 Set Theory and Sizes of Sets How can we say that two sets are the same size? Easy for finite sets (count them)--what about infinite sets? Georg Cantor (1845-1918), who invented Set Theory, proposed a way of comparing the sizes of two sets that does not involve counting how many things are in each Works for both finite and infinite SET SIZE EQUALITY: Two sets are the same size if there is a bijective (injective and surjective) function mapping from one to the other Intuition: neither set has any element left over in the mapping
4 Injective and Surjective f 1 2 3 4 a Sequences of a s Natural numbers aa aaa aaaa f is: a) b) c) d) Injective Surjective Bijective (both (a) and (b)) Neither
5 Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Evens? 1 2 3 4 2 4 6 8 Positive evens Natural numbers A. Yes and my function is bijective B. Yes and my function is not bijective C. No (explain why not)
6 Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Evens? f 1 2 3 4 2 4 6 8 Positive evens Natural numbers f(x)=2x
7 Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Odds? 1 2 3 4 1 3 5 7 Positive odds Natural numbers A. Yes and my function is bijective B. Yes and my function is not bijective C. No (explain why not)
8 Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Odds? f 1 2 3 4 1 3 5 7 Positive odds Natural numbers f(x)=2x-1
9 Countably infinite size sets So | | = |Even|, even though it seems like it should be | | = 2|Even| Also, | | = |Odd| Another way of thinking about this is that two times infinity is still infinity Does that mean that all infinite size sets are of equal size?
10 It gets even weirder: Rational Numbers (for simplicity we ll do ratios of natural numbers, but the same is true for all Q) += {? ?|?,? } 1/1 2/1 3/1 4/1 5/1 6/1 1/2 2/2 3/2 4/2 5/2 6/2 1/3 2/3 3/3 4/3 5/3 6/3 1/4 2/4 3/4 4/4 5/4 6/4 1/5 2/5 3/5 4/5 5/5 6/5 1/6 2/6 3/6 4/6 5/6 6/6 ...
11 It gets even weirder: Rational Numbers (for simplicity we ll do ratios of natural numbers, but the same is true for all Q) += {? ?|?,? } 1/1 2/1 3/1 4/1 5/1 6/1 1/2 2/2 3/2 4/2 5/2 6/2 1/3 2/3 3/3 4/3 5/3 6/3 1/4 2/4 3/4 4/4 5/4 6/4 1/5 2/5 3/5 4/5 5/5 6/5 1/6 2/6 3/6 4/6 5/6 6/6 ... Is there a bijection from the natural numbers to Q+? A. Yes B. No
12 It gets even weirder: Rational Numbers (for simplicity we ll do ratios of natural numbers, but the same is true for all Q) += {? ?|?,? } 1/1 1 2/1 3 3/1 5 4/1 9 5/1 11 5/2 6/1 1/2 2 2/2 x 3/2 8 4/2 x 1/3 4 2/3 7 3/3 x 4/3 5/3 6/3 1/4 6 2/4 x 3/4 4/4 5/4 6/4 1/5 10 1/6 2/5 3/5 4/5 5/5 6/5 ... 2/6 3/6 4/6 5/6 6/6 6/2
13 Sizes of Infinite Sets The number of Natural Numbers is equal to the number of positive Even Numbers, even though one is a proper subset of the other! | | = |E+|, not | | = 2|E+| The number of Rational Numbers is equal to the number of Natural Numbers | | = | +|, not | +| | |2 But it gets even weirder than that: It might seem like Cantor s definition of same size for sets is overly broad, so that any two sets of infinite size could be proven to be the same size Actually, this is not so
14 Thm. | | != | | Proof by contradiction: Assume | | = | |, so a bijective function f exists between and . Want to show: no matter how f is designed (we don t know how it is designed so we can t assume anything about that), it cannot work correctly. Specifically, we will show a number z in that can never be f(n) for any n, no matter how f is designed. Therefore f is not surjective, a contradiction. f ? ? ? z ? 1 2 3 4 Real numbers Natural numbers
15 Thm. | | != | | Proof by contradiction: Assume | | = | |, so a bijective function f exists between and . We construct z as follows: z s nth digit is the nth digit of f(n), PLUS ONE* (*wrap to 1 if the digit is 9) Below is an example f What is z in this example? a) .244 b) .134 c) .031 d) .245 n 1 2 3 f(n) .100000 .333333 .314159
16 Thm. | | != | | Proof by contradiction: Assume | | = | |, so a bijective function f exists between and . We construct z as follows: z s nth digit is the nth digit of f(n), PLUS ONE* (*wrap to 1 if the digit is 9) Below is a generalizedf n 1 2 3 f(n) .d11d12d13d14 .d21d22d23d24 .d31d32d33d34 What is z? a) .d11d12d13 b) .d11d22d33 c) .[d11+1] [d22+1] [d33+1] d) .[d11+1] [d21+1] [d31+1]
17 Thm. | | != | | Proof by contradiction: Assume | | = | |, so a bijective function f exists between and . How do we reach a contradiction? Must show that z cannot be f(n) for any n How do we know that z f(n) for any n? a) We can t know if z = f(n) without knowing what f is and what n is b) Because z s nth digit differs from n s nth digit c) Because z s nth digit differs from f(n) s nth digit n 1 2 3 f(n) .d11d12d13d14 .d21d22d23d24 .d31d32d33d34
Thm. || != || Proof by contradiction: Assume | | = | |, so a correspondence f exists between N and . Want to show: f cannot work correctly. Let z = [z s nth digit = (nth digit of f(n)) + 1]. Note that z , but n , z != f(n). Therefore f is not surjective, a contradiction. So | | | | | | > | |
Diagonalization n 1 f(n) .d11d12d13d14d15d16d17d18d19 .d21d22d23d24d25d26d27d28d29 .d31d32d33d34d35d36d37d38d39 .d41d42d43d44d45d46d47d48d49 .d51d52d53d54d55d56d57d58d59 .d61d62d63d64d65d66d67d68d69 .d71d72d73d74d75d76d77d78d79 .d81d82d83d84d85d86d87d88d89 .d91d92d93d94d95d96d97d98d99 2 3 4 5 6 7 8 9 19
20 Some infinities are more infinite than other infinities Natural numbers are called countable Any set that can be put in correspondence with is called countable (ex: E+, +). Equivalently, any set whose elements can be enumerated in an (infinite) sequence a1,a2, a3, Real numbers are uncountable Any set for which cannot be enumerated by a sequence a1,a2,a3, is called uncountable But it gets even weirder There are more than two categories!
21 Some infinities are more infinite than other infinities | | is called 0 o |E+| = | | = 0 | | is maybe 1 o Although we just proved that | | < | |, and nobody has ever found a different infinity between | | and | |, mathematicians haven t proved that there are not other infinities between | | and | |, making | | = 2 or greater o In fact, it can be proved that such theorems can never be proven Sets exist whose size is 0, 1, 2, 3 An infinite number of aleph numbers! o An infinite number of different infinities
22 Famous People: Georg Cantor (1845-1918) His theory of set size, in particular transfinite numbers (different infinities) was so strange that many of his contemporaries hated it Just like many CSE 20 students! scientific charlatan renegade corrupter of youth utter nonsense laughable wrong disease I see it, but I don't believe it! Georg Cantor himself The finest product of mathematical genius and one of the supreme achievements of purely intellectual human activity. David Hilbert