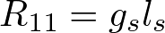Dp-branes, NS5-branes, U-duality, and M-Theory Overview
Overview of Dp-branes, NS5-branes, and U-duality derived from nonabelian (2,0) theory with Lie 3-algebra. Introduction to M-theory, including M2-branes and M5-branes in the strong coupling limit. Discussion on BLG theory, Lorentzian Lie 3-algebra, and the ABJM theory for M2-branes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Dp-branes, NS5-branes and U-duality from nonabelian (2,0) theory with Lie 3-algebra ( , KEK) arXiv: 1103.1327[hep-th]; JHEP 1104 (2011) 117 ( ,KEK) (KEK) seminar@Kyoto University, June 15, 2011
Introduction What is M-theory? 11d SUGRA at low energy [Cremmer-Julia-Sherk] Strong coupling limit of IIA superstring theory Include M2-branes and M5-branes (no strings, F-strings = wrapped M2-branes) According to the M-theory/type IIA duality, M2-branes = strong coupling limit (IR fixed point) of D2-branes (3d SYM) M5-branes = strong coupling limit (UV fixed point) of D4-branes (5d SYM) 1/26
Introduction BLG theory [Bagger-Lambert, Gustavsson] field contents: 8 scalars + Chern-Simons gauge field + fermions Novelty is the appearance of new algebraic structure, Lie 3-algebra \begin{align*} f^{abcd} \end{align*} : antisymmetric Fundamental idenity (generalization of Jacobi identity) \begin{align*} \delta X^I= \Lambda_{ab}[T^a,T^b,X^I] \end{align*} for the closure of gauge transformation This identity is highly restrictive and a few examples are known 2/26
Introduction \begin{align*} {\cal{N}}=8 \end{align*} 3d , finite dim. \begin{align*} f^{abcd}\propto \epsilon^{abcd} \end{align*} \begin{align*} A_4 \ \textrm{BLG} \end{align*} positive norm negative norm \begin{align*} \textrm{Lorentzian BLG} \end{align*} [Ho-Imamura-Matsuo][Gomis et al.] [Benvenuti et al.] Lorenrzian Lie 3-algebra \begin{align*} [u_0,T^i,T^j]=f^{ij}_{ \ \ k}T^k \nonumber \\ [T^i,T^j,T^k]=f^{ijk}v_0 \nonumber \\ \textrm{tr}(u_0,v_0)=-1, \ \ \textrm{tr}(T^i,T^j)=\delta^{ij} \end{align*} \begin{align*} v_0: \textrm{center}, \ \ u_0: \textrm{identity} \nonumber \\ T^i: \textrm{Lie algebra} \end{align*} Component associated to Lorentzian generator becomes ghosts But are Lagrange multipliers and these can be integrated out constraint equation: constant solution (VEV) 3d N=8 SYM (D2-brane) novel Higgs mechanism [Mukhi-Papageorgakis] 3/26
Introduction On the other hand, from the brane construction, the low energy effective action of arbitrarly of M2-branes is proposed ABJM theory [Aharony-Bergman-Jafferis-Maldacena] U(N) U(N) (or SU(N) SU(N)) Chern-Simons-matter theory \begin{align*} {\cal{N}}=6 \end{align*} \begin{align*} S=\int d^3x \Big[ -\textrm{tr} \{ (D_{\mu}Z^A)^{\dagger}D^{\mu}Z^A+(D_{\mu}W^A)^{\dagger}D^{\mu}W^A \} -V(Z,W) \nonumber \\ +\frac{k}{4\pi}\epsilon^{\mu\nu\lambda} \textrm{tr} \{A^{(1)}_{\mu}\partial_{\nu}A^{(1)}_{\lambda}+\frac{2i}{3}A^{(1)}_{\mu}A^{(1)}_{\nu}A^{(1)}_{\lambda}-A^{(2)}_{\mu}\partial_{\nu}A^{(2)}_{\lambda}-\frac{2i}{3}A^{(2)}_{\mu}A^{(2)}_{\nu}A^{(2)}_{\lambda} \} \Big] \end{align*} \begin{align*} \textrm{M2-brane} \end{align*} \begin{align*} {\mathbb{C}}^4/{\mathbb{Z}}_k \end{align*} \begin{align*} \frac{2\pi}{k} \end{align*} N M2-branes on an orbifold \begin{align*} {\mathbb{C}}^4/{\mathbb{Z}}_k \end{align*} (from an analysis of moduli space) \begin{align*} (y^1,y^2,y^3,y^4) \rightarrow (e^{\frac{2\pi i}{k}}y^1,e^{\frac{2\pi i}{k}}y^2,e^{\frac{2\pi i}{k}}y^3,e^{\frac{2\pi i}{k}}y^4) \end{align*} \begin{align*} \mathbb{Z}_{k} : \end{align*} Lorentzian BLG theory can be derived from ABJM theory [YH-Iso-Sumitomo-Zhang 08] 4/26
Introduction Gauge tr. of bifundamental matter field Take a linear combination of generators SU(N) trans. ( in N=2, ISO(3) ) \begin{align*} \tilde{T}^{ab}X=[T^a,T^b,X] \end{align*} Gauge structure of L-BLG \begin{align*} T^a=\{v_0,u_0,T^i \} \end{align*} \begin{align*} [\tilde{T}^{0i},\tilde{T}^{0j}]=if^{ij}_{ \ \ k}\tilde{T}^{0k}, \nonumber \\ [\tilde{T}^{0i},S^j]=if^{ij}_{ \ \ k}S^k, \nonumber \\ [S^i,S^j]=0 \end{align*} \begin{align*} v_0: \textrm{center} \nonumber \\ u_0: \textrm{identity} \nonumber \\ T^i: \textrm{Lie algebra} \end{align*} \begin{align*} [u_0,T^i,T^j]=f^{ij}_{ \ \ k}T^k \nonumber \\ [T^i,T^j,T^k]=f^{ijk}v_0 \end{align*} \begin{align*} S^i \equiv f^i_{ \ jk} \tilde{T}^{jk} \end{align*} 5/26
Introduction ABJM action \begin{align*} S=\int d^3x \Big[ -\textrm{tr} \{ (D_{\mu}Z^A)^{\dagger}D^{\mu}Z^A+(D_{\mu}W^A)^{\dagger}D^{\mu}W^A \} -V(Z,W) \nonumber \\ +\frac{k}{4\pi}\epsilon^{\mu\nu\lambda} \textrm{tr} \{A^{(1)}_{\mu}\partial_{\nu}A^{(1)}_{\lambda}+\frac{2i}{3}A^{(1)}_{\mu}A^{(1)}_{\nu}A^{(1)}_{\lambda}-A^{(2)}_{\mu}\partial_{\nu}A^{(2)}_{\lambda}-\frac{2i}{3}A^{(2)}_{\mu}A^{(2)}_{\nu}A^{(2)}_{\lambda} \} \Big] \end{align*} scaling limit \begin{align*} Z_0 \rightarrow \lambda^{-1}Z_0 \nonumber \\ B_{\mu} \equiv \frac{A_{\mu}^{(1)}-A_{\mu}^{(2)}}{2} \rightarrow \lambda B_{\mu} \nonumber \\ k \rightarrow \lambda^{-1}k \end{align*} \begin{align*} (\lambda \rightarrow 0) \end{align*} L-BLG action \begin{align*} \textrm{VEV} \ Z_0 \rightarrow \infty \ : \textrm{brane is far from origin} \nonumber \\ k \rightarrow \infty \ : {\mathbb{Z}}_k \rightarrow U(1) \textrm{identification} \nonumber \\ B_{\mu} \rightarrow 0 \ : \end{align*} \begin{align*} \frac{2\pi}{k} \end{align*} M2 \begin{align*} {\mathbb{C}}^4/{\mathbb{Z}}_k \end{align*} \begin{align*} S^1 \textrm{compactification} \end{align*} 6/26
Introduction World volume theories of M2-branes (BLG theory, ABJM theory) and their relationships has been intensely studied and generate many interesting development (AdS/CMP, integrability, localization, ) What about M5-branes? low energy dynamics of M5-brane is thought to be described by a 6D theory which has supersymmetry SO(5)R symmetry Conformal symmetry field contents are 5 scalars, a self dual 2-form and fermions [(2,0) tensor multiplet] Deriving self dual 2-form from action principle is difficult and only the abelian (single M5-brane) case is known[Aganagic et.al.][Bandos et.al.] But recently a new approach toward the nonabelianization is proposed and our work is exploration of its properties 7/26
Outline Introduction (2,0) SUSY in 6D Dp&NS5 from (2,0) theory Aspects of U-duality Conclusion and Discussion
(2,0) SUSY in 6D Abelian (2,0) theory linear SUSY transformations are Recently, N. Lambert and C. Papageorgakis generalize this to non-Abelian case with Guiding principle is the emergence of the 5D SYM SUSY transformaion under the reducion 8/26
(2,0) SUSY in 6D Introduce a new (auxiliarly) field Lie 3-algebra naturally appear once again And the proposed SUSY transformations of non-Abelian (2,0) theory are In the following discussions, we treat to be totally antisymetric This SUSY trans. respects SO(5)R and dilatation symmetry (appropriate as the M5-brane theory) 9/26
Non-Abelian (2,0) theory proposed non-Abelian (2,0) SUSY transformation closes under the following EOM and constraints We can recover 5D SYM(D4-brane) by taking a VEV (double) dimensional reduction occurs KK-tower along the M-direction doesn t appear Instantons as KK-states in 5d SYM? [Lambert-Papageorgakis-Schmidt Sommerfeld 10][Douglas 10] 10/26
Non-Abelian (2,0) theory Absence of Consider the introduction of such that Substituting VEV into the constraint we obtain On the other hand, by definition, Comparing the derivative terms leads to and nonlinear part require However, this contradicts the Jacobi identity 11/26
Dp-branes from (2,0) theory Now we start with generalized loop algebra [Ho-Matsuo-Shiba 09][Kobo-Matsuo-Shiba 09] This can be regarded as the original Lorentzian Lie 3-algebra including loop algebra ( in d=1, Kac-Moody algebra ) This central extension is crucial to realize the torus compactification This type of BLG theory can be obtained by the scaling limit of the orbifolded ABJM theory [YH-Zhang 09] 12/26
Dp-branes from (2,0) theory we apply this algebra to the nonabelian (2,0) theory with Lie 3-alebra first we expand the fields as ghost scalar field (and gauge field ) Higgs auxiliarly field auxiliarly field gauge field component EOM We choose VEV s as 13/26
Dp-branes from (2,0) theory Physical meaning of setting the VEV as M5-brane torus compactification along the I directions ( 5 M-direction) D4-brane Dp-brane (p>4) These VEVs corresponds to the moduli parameter of torus compactification radius of M-circle + moduli of and the metric of torus is determined by It is convenient to use the projection operator which determine how to decompose into and bocomes fiber direction of Dp-brane w.v. Later we will see that is actually compactified on 14/26
Dp-branes from (2,0) theory component field and constraints dimensional reduction of M-direction (M5 D4) scalar field Using projection operator , we decompose the scalar fields as (gauge field of fiber direction) Then we obtain the kinetic part of gauge field (of fiber direction) and scalar field spinor field 15/26
Kaluza-Klein mass by Higgs mechanism In this stage, we can see how the higher dim. (p>4) Dp-brane theory arise In D4-brane perspective, this theory has mass term KK-tower similar mass terms exist for all the fields with index If we define gamma matrices of new direction as , they satisfy and Therefore, through the Fourier transformation, we obtain Same procedure works out and we can construct higher dimensional fields defined by Finally we obtain D(d+4)-brane whose worldvolume is 16/26
Dp-branes from (2,0) theory gauge field self dual 2-form We substitute the EOM of gauge field and the self duality conditon into the EOM of self dual 2-form Then we obtain the EOM of the Yang-Mills gauge field 17/26
Dp-branes from (2,0) theory We finally obtain the following EOM These are precisely the EOM of (5+d)D SYM !! We derive the equations of motion of Dp-brane whose world volume is from nonabelian (2,0) theory with Lie 3-algebra 18/26
NS5-branes from (2,0) theory So far, we consider only the reduction to the Dp-brane Type IIA NS5-brane is obtained by choosing VEV s as In this case dimensional reduction by doesn t occur because of the absence of the VEV of So the world volume remains to be (1+5)D Finally we obtainded the simple copies of the free (2,0) tensor multiplet (no interaction terms) For the Type IIB NS5-brane, the dimensional reduction occurs but another direction of world volume appears and resulting theory becomes (1+5)D Moreover, in this case, we can read the string coupling from the gauge field and this enables us to check the S-duality between NS5-brane and D5-brane 19/26
IIB NS5-branes from (2,0) theory We start with Lorentzian Lie 3-algebra with Kac-Moody algebra And we choose the VEV as M5-brane compactification along 5 direction ( 10 M-direction) IIA NS5-brane IIB NS5-brane and reformulate the fields in a slightly different way from the previous case as This is because, in order to obtain IIB NS5-brane, we interchange the M-direction and T-duality direction in the D5-brane case 20/26
IIB NS5-branes from (2,0) theory Emergence of additional world volume direction For example, EOM of scalar field of 10 direction is This was an auxiliarly field in the Dp-brane case but now this becomes a gauge field on the IIB NS5-brane Together with the identification and we finally obtain the expected EOM of extra gauge field Other EOMs are similarly obtained and they are all consistent with the (1,1) vector multiplet of IIB NS5-brane 21/26
D5-brane on S^1 First we consider the simplest case, D5-branes on ( M-theory compactified on ) In this case, the U-duality group is T-duality VEV corresponds with the compactification radius of M-direction as and the radius of transverse direction T-duality acts is (in D4-brane point of view) On the other hand, we have obtained the D5-brane action given by and these are consitent with the expected T-duality relation (note that the world volume of fiber direction of D5-brane is a dual circle) 22/26
D5-brane on S^1 for the IIB NS5-brane, we can read the string coupling from the coefficient of the kimetic term of gauge field This is the inverse of the string coupling in D5-brane theory and we see that the S-transformation is represented by the rotation of VEV T-transformation automorphism of Lie 3-algebra Therefore, we can realize the SL(2,Z) transformaion as a rotation of the VEV, as expected 23/26
Dp-brane on T^(p-4) Then we consider general case, Dp-branes on ( M-theory compactified on ) In this case, we can realize the moduli parameter as In general, the U-duality group is and part of it can be realized by the transformaion of VEV s as However, we cannnot reproduce all the moduli parameters, at least in our set up 24/26
Dp-brane on T^(p-4) Realization of the moduli parameter d Background fields Parameter sp. D5 1 D6 2 D7 3 D8 4 D9 5 : NS-NS 2-form deformation of 3-algebra?? : R-R form field ?? 25/26
Conclusion and Discussion We derive Dp&NS5 from nonabelian (2,0) theory with Lie 3-algebra As a consistency check, we see that the expected U-duality relations are correctly reproduced In paricular, we realize the S-duality between IIB NS5 D5 It is known that the Lorentzian BLG theory are derived from the scaling limit of the ABJM theory and it is just conceivable that certain quiver gauge theory has a origin of nonabelian (2,0) theory with Lie 3-algebra (but in general the inverse process of scaling limit is not so easy) A M5-brane in 3-form flux can be constructed from BLG theory [Ho-Imamura-Matsuo-Shiba] It includes interaction terms like Adding flux in nonabelian (2,0) theory with Lie 3-algebra may be interesting 26/26
PST action PST action [Bandos et.al.] Fixing the additional gauge sym. as , we obtain the following non-covariant action [Aganagic et.al.] From the eom of , we get Solution : As a gauge fixing condition of we obtain