Understanding Angles and Angle Classification
Explore the world of angles with illustrations of lines, rays, and segments. Learn about acute, right, obtuse, and straight angles, as well as concepts like congruent and vertical angles. Discover how to name angles and understand their measures based on degrees in a clear and structured manner.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Draw the following: Line AB Line segment BC Ray FG
An angle is the union of two rays that share a common endpoint.
There are 4 ways to name an angle: CED DEC E 3
Acute angles have measures between 0 and 90 degrees
Right angles have measures of exactly 90 degrees (indicated by a small square)
Obtuse angles have measures between 90 and 180 degrees
Right angle Straight angle Acute angle Obtuse angle
Congruent angles are angles of the same measure(indicated by identical markings)
Similar to the ruler postulate, if point B is in the interior of AOC, then m COB+m BOA=m COA (<AOC)
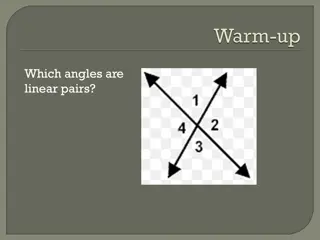
Vertical angles are opposite congruent angles created by the intersection of two lines <1 and <3 are vertical angles <2 and <4 are vertical angles
Adjacent angles are angles that share a common side, common vertex, and no common interior points. <KIH and <KIJ are adjacent angles
Complementary angles are two angles whos measures sum to 90 . <TSU and <USV are complementary angles. If m<TSU=42 , what is m<USV? <TSU is the complement of <USV
Supplementary angles are two angles whos measures sum to 180 . <TSU and <USV are supplementary angles. <TSU is the supplement of <USV. If m<TSU=120 , what is m<USV?
Use the adjacent angles below to solve the following: m<HOK = 4x-6, m <KOB=6x+2, find x and m<HOK.
Line up the bottom of the protractor with a side of the angle and center of angle with center of protractor. Extend the line of the other side and read the degree.