Understanding the Law of Sines for Finding Missing Side Lengths and Angle Measures
The Law of Sines is a fundamental concept in trigonometry that helps in finding missing side lengths and angle measures of any triangle. Through examples and explanations, this content teaches how to apply the Law of Sines to solve for unknowns in non-right triangles. It covers writing equations, substituting values, and solving for missing variables such as side lengths, angles, and the area of a triangle.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
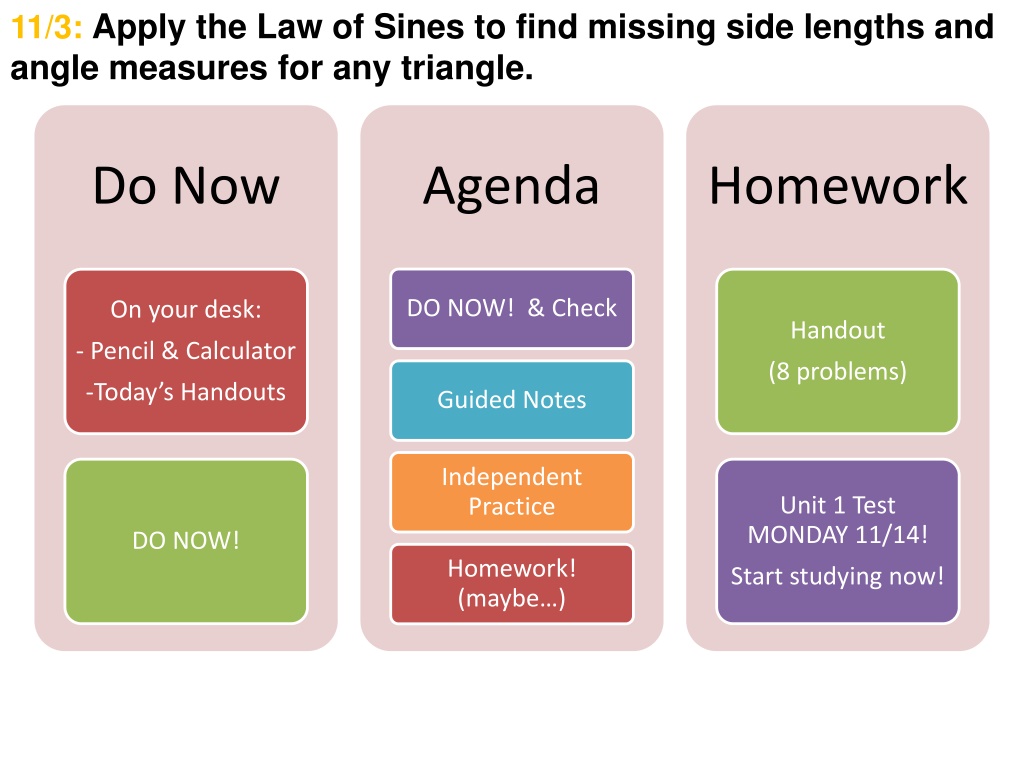
11/3: Apply the Law of Sines to find missing side lengths and angle measures for any triangle. Do Now Agenda Homework DO NOW! & Check On your desk: Handout - Pencil & Calculator (8 problems) -Today s Handouts Guided Notes Independent Practice Unit 1 Test MONDAY 11/14! DO NOW! Homework! (maybe ) Start studying now!
We will learn to Apply Law of Sines to find missing side lengths and angle measures of any triangle.
Law of Sines: sin c sin b sin a = = b C C B A A a c A C B B = = sin c sin a sin b side lengths one side one angle Law of Sines is used to find missing _____________________ when you are given _______________ and _________________. It can also be used to find missing _____________________ when you are given _______________ and _________________. two angles angle measures two sides
Example 1:Find the value of A. Round to nearest tenth. Given: NOT Right Triangle! Write Equation, Substitute, & Solve: b sin c sin a sin b = 39 = C Angle a = 45 Angle b = 39 C A B A 45 Side B= 6 a sin 39 6 6 sin 45 A A = c 6 B Finding: Side A = sin 45 sin 39 A Law of Sines?: Yes! = *sin 45 9.534 *sin 45 sin 45 A= 9.534*sin 45 A 6.7 units
Example 2:Find the value of c. Round to nearest tenth. Given: NOT Right Triangle! Angle b = 70 Write Equation, Substitute, & Solve: b sin c sin a sin b C = = 70 7 C A B A Side B= 9 Side C= 7 a sin c 7 sin 70 9 = c 9 B Finding: Angle c sin c 7 sin c 7* 0.104 *7 = Law of Sines?: Yes! 0.731 = sin-1(0.731) = c c = 46.959 c 47
Example 3:Find the area of the triangle. Round to tenth. Given: NOT Right Triangle! Angle c = 47 Write Equation, Substitute, & Solve: b C sin * side 2 * side 1 Area = A 6 2 Side A= 6 Side B= 9 47 a *9* 6 sin 47 Area c = 9 B 2 Finding: Area of Triangle Area 19.7 units2 Law of Sines?: Yes! (kinda sorta )