Understanding Rotational Kinetic Energy and Moment of Inertia
Rotational kinetic energy arises from the motion of mass in a rotating object, while moment of inertia quantifies an object's resistance to rotational motion. This concept is crucial for analyzing the energy and stability of rotating systems. The content explains the calculation of kinetic energy for rotating objects, moment of inertia for rigid bodies, and how mass distribution affects these properties. The parallel-axis theorem is also introduced to relate moments of inertia about different axes.
- Rotational Kinetic Energy
- Moment of Inertia
- Rotating Systems
- Mass Distribution
- Parallel-Axis Theorem
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
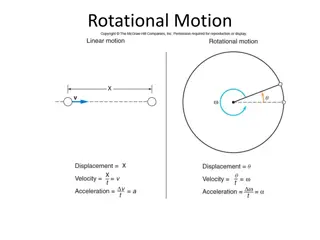
Rotational Kinetic Energy The rotating object consists of mass in motion, so it has kinetic energy Let s consider a body made up of a large number of particles with masses ?1, ?2,?3, at distances ?1, ?2,?3, from the axis of rotation Kinetic energy of an ith particle is 1 2???? 2=1 2??(????)2 Total kinetic energy is 1 2??(????)2=1 2)?2 ? = 2( ???? ? ?
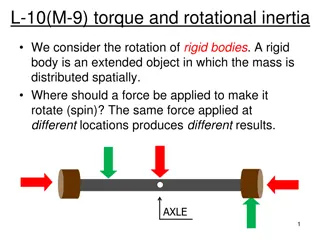
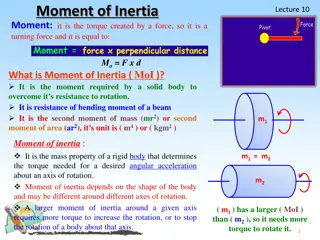
Rotational kinetic energy and moment of inertia The rotational kinetic energy of a rigid body is: ? =1 2??2 The moment of inertia, I, is obtained by multiplying the mass of each particle by the square of its distance from the axis of rotation and adding these products: 2 ? = ?1?12+ ?2?2 2+ ?3?3 2+ = ???? ? The SI unit of I is the 2 2 kilogram-meter (kg m ).
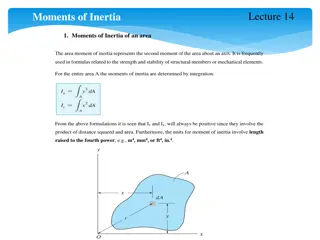
Moment of inertia of continuous distribution of mass The moment of inertia of any distribution of mass can be found by integrating over its volume: ? = ?2??? Using an infinitesimally small piece of mass to calculate the contribution to the total moment of inertia.
Moment of inertia, continued Moment of inertia depends on Mass of an object Size and shape of the object How the mass is distributed Axis of rotation
The parallel-axis theorem There is a simple relationship, called the parallel-axistheorem, between the moment of inertia of an object about an axis through its center of mass and the moment of inertia about any other axis parallel to the original axis. ??= ???+ ??2 (a) A barbell with an axis of rotation through its center; (b) a barbell with an axis of rotation through one end.