Understanding Moments of Inertia in Structural Mechanics
Moments of inertia of an area play a crucial role in determining the strength and stability of structural members and mechanical elements. This includes concepts such as area moment of inertia, parallel-axis theorem, and radius of gyration. The integration process, positive nature, and units of moment of inertia are explained along with practical examples of determining moment of inertia for different area shapes. The content also covers the application of the parallel-axis theorem and calculations related to the centroidal axis and base of shapes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
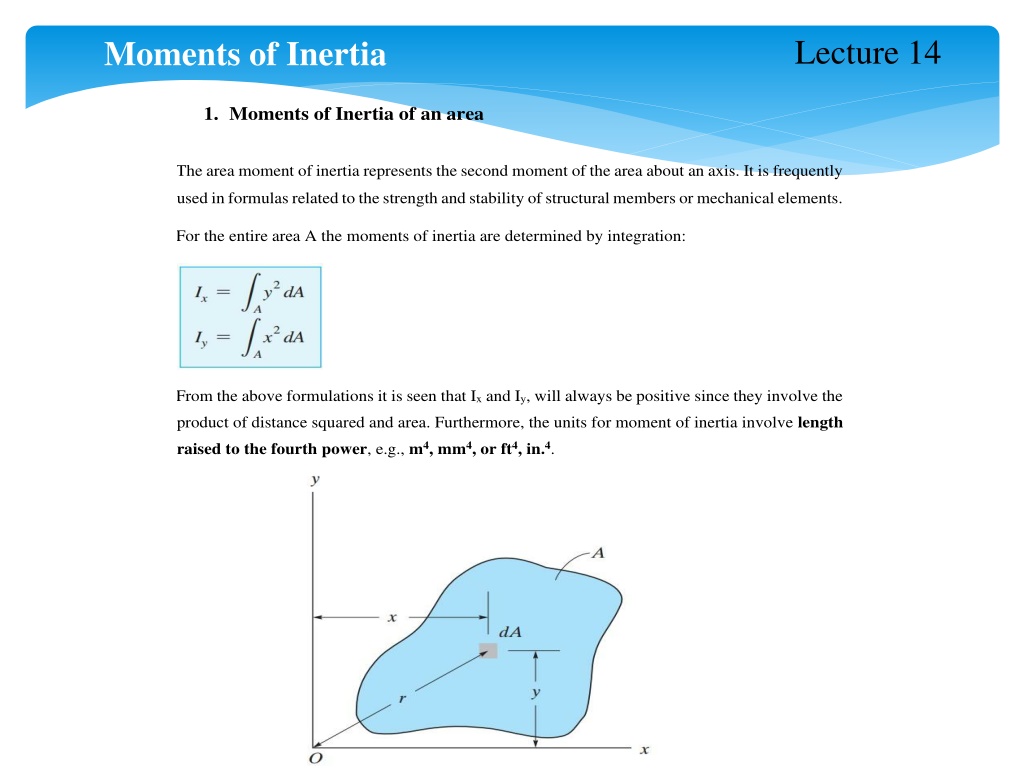
Lecture 14 Moments of Inertia 1.Moments of Inertia of an area The area moment of inertia represents the second moment of the area about an axis. It is frequently used in formulas related to the strength and stability of structural members or mechanical elements. For the entire area A the moments of inertia are determined by integration: From the above formulations it is seen that Ix and Iy, will always be positive since they involve the product of distance squared and area. Furthermore, the units for moment of inertia involve length raised to the fourth power, e.g., m4, mm4, or ft4, in.4.
1.Parallel-Axis Theorem for an Area The parallel-axis theorem can be used to find the moment of inertia of an area about any axis that is parallel to an axis passing through the centroid and about which the moment of inertia is known. ? X and? y : The first integral represents the moment of inertia of the area about the centroidal axis. A:The total area. dy and dx:The distance between the parallel x and x and y and y respectively. 2.Radius of Gyration of an Area The radius of gyration of an area about an axis has units of length and is a quantity that is often used for the design of columns in structural mechanics. Provided the areas and moments of inertia are known, the radii of gyration are determined from the formulas
EXAMPLE: Determine the moment of inertia for the rectangular area shown in Fig. 105 with respect to (a) the centroidal x axis, and (b) the axis xb passing through the base of the rectangle. SOLUTION:
EXAMPLE: Determine the moment of inertia for the shaded area shown in Fig. 106a about the x-axis. SOLUTION:
EXAMPLE: Determine the moment of inertia with respect to the x axis for the circular area shown in Fig. 10 7a.