Parallel axis theorem - PowerPoint PPT Presentation

Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati

1 views • 5 slides

The Coase Theorem, developed by economist Ronald Coase, posits that under certain conditions, bargaining related to property rights will lead to an optimal outcome regardless of the initial distribution. It provides a framework for resolving conflicts by emphasizing negotiation and efficient market

0 views • 10 slides

Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th

3 views • 25 slides

This course material covers Lami's Theorem in Engineering Mechanics taught by Ranbir Mukhya. It includes an outline of the theorem, problem scenarios involving cylinders with given weights and diameters, and the determination of reactions at various points. Detailed force diagrams and calculations a

3 views • 8 slides

Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista

1 views • 14 slides

The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex

2 views • 31 slides

Superposition theorem in electrical circuits states that the effects of multiple voltage and current sources in a network can be analyzed independently and then combined algebraically. This allows for calculating the voltage and current distribution in a network more efficiently. The theorem involve

0 views • 9 slides

Lami's Theorem is an equation that explains how the magnitudes of forces acting on a point keep an object in equilibrium. This theorem relates the forces with corresponding angles and is derived by understanding the sum of forces acting on a point. By utilizing complementary angles and the sine rule

0 views • 8 slides

The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines

0 views • 21 slides

Vertical axis wind turbines (VAWT) include Darrieus, H-Rotor, and Savonius designs, while horizontal axis wind turbines (HAWT) have advantages such as better performance at greater heights and stronger winds. VAWT face challenges like self-starting and commercial success. Both turbine types operate

1 views • 9 slides

Exploring the concepts of parallel sorting algorithms, analyzing parallel programs, divide and conquer algorithms, parallel speed-up, estimating running time on multiple processors, and understanding Amdahl's Law in parallel computing. The content covers key measures of run-time, divide and conquer

3 views • 40 slides

Introduction to Bayes Theorem in Natural Language Processing (NLP) with detailed examples and applications. Explains how Bayes Theorem is used to calculate probabilities in diagnostic tests and to analyze various scenarios such as disease prediction and feature identification. Covers the concept of

0 views • 13 slides

Explore the application of Pythagoras Theorem in solving problems related to right-angled triangles, diagonals of shapes like rectangles and rhombuses, and the height of triangles. Learn how to use Pythagoras Theorem effectively by drawing diagrams, identifying known lengths, and using the theorem t

0 views • 8 slides

The medial axis in geometry is a fascinating concept related to Voronoi diagrams and maximal empty disks. Explore how the medial axis is constructed, its significance in the study of polygons, and its applications in modeling and algorithms. Learn about associated exercises and different algorithms

0 views • 12 slides

Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m

0 views • 45 slides

Rolle's Theorem states that for a continuous and differentiable function on a closed interval with equal function values at the endpoints, there exists at least one point where the derivative is zero. The Mean Value Theorem asserts that for a continuous and differentiable function on an interval, th

0 views • 5 slides

This resource delves into key concepts such as the Mean Value Theorem, Fermat's Theorem, Rolle's Theorem, Extreme Value Theorem, local maximums, and more. It presents important results and explores proofs in the context of analysis.

1 views • 71 slides

Learn about parallel programming directives like Diretiva.parallel and #pragma omp.parallel, which allow code to be executed by multiple threads simultaneously. Explore concepts such as defining parallel regions, setting the number of threads, and utilizing OpenMP directives for parallel for loops.

0 views • 39 slides

In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,

0 views • 13 slides

The Axis Powers, composed of Italy, Japan, and Germany, were established to challenge the existing European order and expand their influence. Through alliances and shared military ambitions, they aimed to dominate different regions of the world during World War II, with Germany targeting Europe, Ita

1 views • 8 slides

This review covers essential topics from the CS260 Parallel Algorithms course by Yihan Sun, focusing on key concepts such as scheduler programs, cost models, reduce and scan techniques, PRAM models, atomic primitives, small algorithms, the master theorem, and sorting algorithms like Quicksort and Me

1 views • 25 slides

Understanding and implementing parallel structure in business communication is essential for clear, effective, and professional writing. Explore the nuances of parallelism, such as using correlative conjunctions like "not only...but also," to ensure consistency and coherence in your written work. Le

0 views • 21 slides

Binomial theorem is a powerful mathematical concept used to expand expressions involving binomials. This presentation explores the basics of binomial expansion, formulae for positive, negative, and fractional indices, along with examples demonstrating its application. By leveraging the binomial theo

1 views • 10 slides

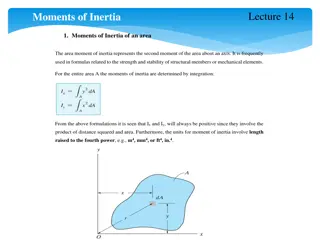
Moments of inertia of an area play a crucial role in determining the strength and stability of structural members and mechanical elements. This includes concepts such as area moment of inertia, parallel-axis theorem, and radius of gyration. The integration process, positive nature, and units of mome

0 views • 5 slides

Dive into the world of automated theorem proving in Lean with a focus on formal verification, history, and the use of logic and computational methods. Explore how programs can assist in finding and verifying proofs, as well as the significance of interactive theorem provers. Discover the evolution o

1 views • 35 slides

This lecture provides a comprehensive overview of parallel approaches for multiobjective optimization in CMPE538. It discusses the design and implementation aspects of algorithms on various parallel and distributed architectures. Multiobjective optimization problems, often NP-hard and time-consuming

0 views • 20 slides

Understanding the inequalities in triangles using the Hinge Theorem. The theorem explains how the length of the third side of a triangle relates to the included angles and congruent sides in different triangle configurations. Explore problems that involve applying the Hinge Theorem and its converse

0 views • 8 slides

This overview delves into the basics of parallel computing, covering parallel memory architectures, programming models, design issues, and parallelizing serial programs. Parallel computing involves leveraging multiple compute resources simultaneously to enhance computational efficiency and solve pro

1 views • 35 slides

Charm++ is a generalized approach to parallel programming that offers an alternative to traditional parallel programming languages like MPI, UPC, and GA. It emphasizes overdecomposition, migratability, and asynchrony to enhance parallel program performance and efficiency. The framework uses indexed

0 views • 43 slides

Dive into the innovative approaches to parallel programming as elucidated by Professor Smruti R. Sarangi from IIT Delhi. The book outlines new paradigms, strategies, and frameworks for designing and optimizing parallel programs. Readers will gain insights into cutting-edge techniques that improve pe

1 views • 52 slides

In this lesson, students will learn about parallel lines and their properties through various examples and explanations. The lesson covers the definition of parallel lines, identifying parallel and non-parallel lines, understanding the concept of transversals, and exploring angles formed by a transv

0 views • 27 slides

The Pythagoras Theorem explains the relationship between the sides of a right-angled triangle. Discover the history, visualization, and application of this fundamental mathematical concept through a detailed exploration. Uncover how to use Pythagoras Theorem to calculate the length of the hypotenuse

0 views • 14 slides

In a geometrical problem involving intersecting lines on the x-axis, we demonstrate the formation of right-angled triangles by applying Pythagoras' theorem. Through visual aids and mathematical explanations, the concept of right angles within triangles is illustrated with clarity and precision.

1 views • 12 slides

Explore the concepts of perpendicular and angle bisectors through the Perpendicular Bisector Theorem, Converse of the Perpendicular Bisector Theorem, Angle Bisector Theorem, and Converse of the Angle Bisector Theorem. Learn how these theorems are applied in geometry with illustrative examples. Get i

0 views • 7 slides

Geometry, Parallel Lines, Triangle Theorem, Angles, Triangles

0 views • 10 slides

Explore parallel prefix algorithms and the PRAM model of parallel computation in the context of turning serial processes into parallel ones. Understand the concepts of vector operations, broadcast, reduction, and examples of prefix functions. Delve into theoretical insights and practical application

0 views • 33 slides

Learn to efficiently implement matrix-vector multiplication using OpenMP for parallel computing, utilizing sparse matrix formats and comparing different parallel computing strategies to optimize performance. The content covers C++ code implementations, thread parallelism with OpenMP, and recruiting

0 views • 48 slides

Explore the world of parallel computing, where multiple processing elements collaborate to solve problems simultaneously. Learn about the key elements of parallel computers, contemporary computing systems, parallel programs, and the reasons why parallel computing is essential for large-scale applica

0 views • 36 slides

Explore the realm of parallel computing, where multiple processing elements collaborate to tackle complex problems simultaneously. Discover the significance of parallel computers in modern computing systems, from mobile devices to supercomputers, and the advantages they offer in terms of efficiency

0 views • 15 slides

Explore the concepts of matrix multiplication, solving recurrences using the Master Theorem, and applications solvable in parallel. Learn about standard iterative matrix multiplication algorithms and how to compute cells in parallel for efficient processing. Stay updated on homework deadlines and ac

0 views • 37 slides