Understanding Area Moment of Inertia and Centroidal Axis in Mechanics
Explore the concept of area moment of inertia and centroidal axis in mechanics through detailed explanations and visual representations. Learn how to determine moment of inertia, locate the centroid, and understand the principles behind mass moment of inertia. Dive into the calculation methods and practical applications of these key concepts in engineering analysis.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
ESC-S201 09-NOV MON.
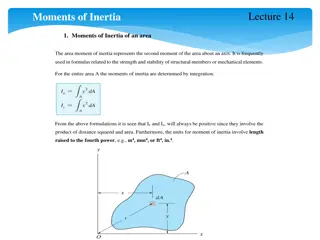
Area moment of inertia Axis o dA is area of element o r is perpendicular distance of elemental area to axis about which area moment of inertia is calculated dA Area moment of inertia ( I ) r I = Area * r2 I = dA * r2
Area moment of inertia Area moment of inertia about x-axis i = n Ixx = dAi * y2i i = 1 Area moment of inertia about x-axis i = n X IYY = dAi * x2i i = 1 Y n tends to infinity.
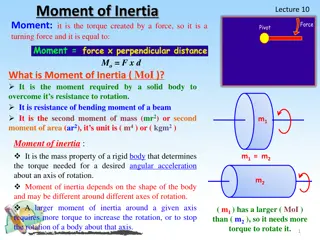
Area moment of inertia Area moment of inertia Mass moment of inertia L L M A G G Centroidal axis Centroidal axis IG = M L2 IG = A L2 12 12
Area moment of inertia Area moment of inertia Mass moment of inertia G G A M Centroidal axis Centroidal axis IG = M R2 IG = A R2 4 4
Area moment of inertia 1. Determine the moment of inertia of the section about an axis passing through the centroid and parallel to the top most fiber of the section. 140 10 140 10
Locate the centroid Axis of symmetry Locus of G Centroid lie on axis of symmetry
Locate the centroid Y- axis Section-1 xG 0 yG 70 140 Section-1 G1 70 X- axis O Centroid lie on axis of symmetry
Locate the centroid Section-2 Y- axis G2 10 xG 0 yG 145 140 Section-2 X- axis O Centroid lie on axis of symmetry
Locate the centroid Y- axis G2 Section Area (mm2) Centroid Ai * xi Ai * yi xc yc (mm) Section-1 ( mm3 ) A1 * xG1 0 ( mm3 ) (mm) I A1 xG1 0 yG1 70 A1 * yG1 9800 1400 II A2 1400 xG2 0 yG2 145 A2 * xG2 0 A2 * yG2 X- axis 203000 O xG 0 yG 70 Section-1 xG 0 yG 145 Section-2 Centroid lie on axis of symmetry
Locate the centroid Y- axis Section Area (mm2) Ai * xi Ai * yi Centroid xc yc (mm) ( mm3 ) ( mm3 ) (mm) I 1400 0 70 0 9800 II 1400 0 145 0 203000 0 2800 212800 G 6 G1 Centroid of the Section xG yG 70 0 76 X- axis O 212800 yG = 2800
Moment of inertia Y- axis G2 d2 G IG d1 6 IG1 G1 70 IG = ( IG1 + A1 d12 ) + ( IG2 + A2 d22 )
G2 d2 IG G G IG 6 IG1 G1 d1 6 L1 =140 IG1 G1 70 70 10 Section -1 A1d12 IG1 + A1d12 = 171966.67 mm4 Length width Area d1 IG1 L1 140 mm 10 mm 1400 mm2 140 mm = 1400 x 6 = 8400 mm4 (A1L12 )/12 YG YG1 = (1400* 1402 )/12 = 76 70 = 163566.67 mm4 = 6 mm IG = ( IG1 + A1 d12 ) + ( IG2 + A2 d22 )