Understanding Conservation Laws in Rotational Energy
Explore the concept of conservation laws in rotational energy, delving into the principles of mechanical energy and angular momentum conservation to solve rotational problems. Learn how to apply vector mathematics, kinetic energy formulas, and potential energy variations in frictionless systems. Master the dynamics of rotating bodies, rolling motion, and the intriguing combination of rotation and translation in rolling objects like wheels and spheres.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
CONSERVATION LAWS PHY1012F PHY1012F ROTATION II ROTATION II Gregor Leigh gregor.leigh@uct.ac.za
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROTATIONAL ENERGY Learning outcomes: At the end of this chapter you should be able to Use the laws of conservation of mechanical energy and angular momentum to solve rotational problems, including those involving rolling motion. Use vector mathematics to describe and solve problems involving rotational problems. 2
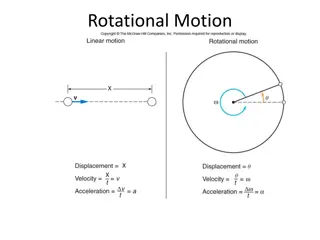
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROTATIONAL ENERGY Each particle in a rigid rotating body has kinetic energy. m2 r3 m3 r2 The sum of all the individual kinetic energies of each of the particles is the rotational kinetic energy of the body: Krot = m1v12 + m2v22+ r1 axle m1 Krot = m1r12 2 + m2r22 2+ Krot = ( m1r12) 2 Krot = I 2 3
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY CONSERVATION OF ENERGY As usual, energy is conserved (in frictionless systems). If, however, a horizontal axis of rotation does not coincide with the centre of mass, the object s potential energy will vary. axle So we write: Emech = Krot + Ug = I 2 + MgyCM K U Emech=K+U Emech=0 4
PHY1012F ROTATION OF A RIGID BODY NEWTON S LAWS ROTATION ABOUT A FIXED AXIS A 70 g metre stick pivoted freely at one end is released from a horizontal position. At what speed does the far end swing through its lowest position? pivot i= 0 rad i= 0 rad/s f2= i2 + 2 f2= 0 + 2( 15)( 0.5 ) 15 = = = 15 rad/s2 (Not constant) = = 6.8 rad/s f vt = r vt = 6.8 1 = 6.8 m/s f= 0.5 rad f= ? 7. Use rotational kinematics to find angular positions and velocities. (Not thistime!) 5
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY A 70 g metre stick pivoted freely at one end is released from a horizontal position. At what speed does the far end swing through its lowest position? y L = 1 m pivot x M = 0.07 kg yCM = 0 m 0 = 0 rad/s Before: I 02 + MgyCM 0 = I 12 + MgyCM 1 ( ( 2 3 1 0 ML = = ) ) ( ( ) ) yCM = 0.5 m 1 = ? vtip = ? After: 2 2 + + Mg L 1 1 1 2 3g L = = 1 = = = = = = v L g L 3 5.42 m/s tip 1 6
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROLLING MOTION Rolling is a combination of rotation and translation. (We shall consider only objects which roll without slipping.) As a wheel (or sphere) rolls along a flat surface 2 R each point on the rim describes a cycloid; the axle (the centre of mass) moves in a straight line, covering a distance of 2 R each revolution; the speed of the wheel is given by 2 R T = = = = R v CM 7
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY FUNNY THING ABOUT THE CYCLOID If a farmer s road surface were rutted into a cycloid form, the smoothest way to get his sheep to market would be to use a truck with SQUARE wheels! 8
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROLLING MOTION The velocity of a particle on a wheel consists of two parts: v v = = + + v i i CM , rel TRANSLATION + ROTATION = ROLLING v=2vCM =2 R R vCM v = R vCM + = 0 v = 0 R vCM P So the point, P, at the bottom of an object which rolls (without slipping) is instantaneously at rest 9
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY KINETIC ENERGY OF A ROLLING OBJECT If we regard P as an instantaneous axis of rotation, the object s motion simplifies to one of pure rotation, and thus its kinetic energy is given by: v=2 R K =Krot about P = IP 2 v = R Using the parallel axis theorem, IP = (ICM + MR2) v = 0 K = ICM 2 + M(R )2 P K = ICM 2 + M(vCM)2 K =Krot + KCM I.e. 10
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY THE GREAT DOWNHILL RACE Kf = Ui ICM 2 + M(vCM)2 = Mgh v h CM R ) ) = = ICM = cMR2 and 2 + + v ( ( 2 2 CM R = = cMR M v Mgh 1 1 CM 2 2 ) )( ( c v ) ) 2 ( ( + + = = M Mgh 1 1 CM 2 gh + + 2 1 = = v ( ( ) ) c CM I.e. The actual values of M and R do not feature, but where the mass is situatedis of critical importance. 11
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY THE GREAT DOWNHILL RACE 2 1 c + + gh = = v ( ( ) ) CM vCM2 = 0 + 2a x where x h h = = x sin ( ( ) ) x 2 gh 2 v g sin 1 + + ( ( ) ) c + + CM 2 1 = = = = = = a CM c h 2 sin a particle 1 + + = = a CM c I.e. The acceleration of a rolling body is less than that of a particle by a factor which depends on the body s moment of inertia. 12
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY VECTOR DESCRIPTION OF ROTATIONAL MOTION Using only clockwise and counterclockwise is the rotational analogue of using backwards and forwards in rectilinear kinematics. A more general handling of rotational motion requires vector quantities. The vector associated with a rotational quantity has magnitude equal to the magnitude of that quantity; has direction as given by the right-hand rule. E.g. The angular velocity vector, , of this anticlockwise-turning disc points in the positive z-direction. 13
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY THE CROSS PRODUCT F The magnitude of the torque exerted by force applied at displacement from the turning point is: rFsin r Once again, the quantity rFsin is the product of two vectors, and , at an angle to each other. This time, however, we use the orthogonal components to determine the cross product of the vectors: . i i = j j = k k = 0 ( ( r F r F y ) ) i = = k j i 1 = = j In RH system: j ( ( ( ( ) ) ) ) x i j k i j k = = = = k 1 1 z j i k k i = = = = 14
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY THE CROSS PRODUCT = = r F rF sin Notes: The more orthogonal the vectors, the greater the cross product; the more parallel, the smaller F r Since it is a vector quantity, the cross product is also known as the vector product. ( ( ) ) A B C A B A C + = + + = + . Derivative of a cross product: ( ( ) ) r p dt dp dt d dr dt = = + + p r 15
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ANGULAR MOMENTUM We have shown that in circular motion (where vt and r are perpendicular) a particle has angular momentum L = mrvt. mvt = p L = rp z = = p p mv r More generally (allowing for and to be at any angle ) p r = (mrvsin , direction from RH rule) ) ) p p r dt dt = = d dt L dL dt r p ( ( dp dr = = = = + + = = + + r v p r F net dp dt dL dt = = F I.e. (Cf. in linear motion: ) = = net net 16
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROTATIONAL MOMENTUM & ENERGY Summary of corresponding quantities and relationships: Linear Rotational Krot = I 2 KCM = MvCM2 (around an axis of symmetry) = = P Mv = = I L CM dP dt dL dt = = = = F net net P L Linear momentum, , is con- served if there is no net force Angular momentum, , is con- served if there is no net torque 17
PHY1012F CONSERVATION LAWS ROTATIONAL ENERGY ROTATIONAL ENERGY Learning outcomes: At the end of this chapter you should be able to Use the laws of conservation of mechanical energy and angular momentum to solve rotational problems, including those involving rolling motion. Use vector mathematics to describe and solve problems involving rotational problems. 18