Understanding Rotational Motion in Chapter 10
Exploring the concepts of rotational motion in a rigid object, focusing on angular displacement, velocity, acceleration, torque, and moment of inertia. Key topics include angular quantities, relationships between linear and angular motion, and applications in calculating rotational parameters. Practice problems and illustrations enhance comprehension.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Chapter 10:Rotation of a rigid object about a fixed axis Reading assignment: inertia, don t worry about integral calculation), 10.6 to 10.9 Chapter 10.1 to10.4, 10.5 (know concept of moment of Homework 10.1 (due Thursday, Nov. 1): CQ9, CQ10, AE1, 2, 6, 12 Homework 10.2 (due Thursday, Nov. 1): 15, 21 Homework 10.3 (due Thursday, Nov. 1): 27, 28 Rotational motion Angular displacement, angular velocity, angular acceleration Torque Rotational energy Moment of Inertia
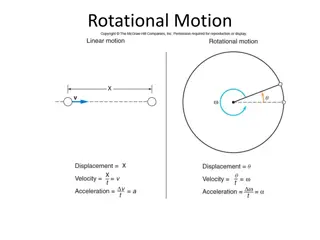
Rotational motion Look at one point P: = r s Arc length s: Thus the angle (angular position) is: s r = Planar, rigid object rotating about origin O. is measured in degrees or radians (SI unit: radian) Radian degrees 2 1 360 180 90 57.3 Full circle has an angle of 2 radians. Thus, one radian is 360 /2 =
Define quantities for circular motion (note analogies to linear motion!!) = Angular displacement: f i f i = = Average angular speed: t t t f i d = = Instantaneous angular speed: lim t dt 0 t f i = = Average angular acceleration: t t t f i d = = Instantaneous angular acceleration: lim t dt 0 t
Angular velocity is a vector Right-hand rule for determining the direction of this vector. Every particle (of a rigid object): rotates through the same angle, characterize rotational motion of entire object has the same angular velocity, has the same angular acceleration.
Rotational motion with constant rotational acceleration, Linear motion with constant linear acceleration, a. Exactly the same equations, just different symbols!! = + = + v v a t t xf xi x f i = + + = + + 1 1 ( ) ( ) x x v v t t f i xi xf f i i f 2 2 1 1 = + + = + + 2 2 x x v t a t t t f i xi x f i i 2 2 2 2 2 2 = + = + 2 ( ) 2 ( ) v v a x x xf xi x f i f i f i
Black board example 10.1 A wheel starts from rest and rotates with constant angular acceleration and reaches an angular speed of 12.0 rad/s in 3.00 s. 1. What is the magnitude of the angular acceleration of the wheel (in rad/s2)? 2. Through what angle does the wheel rotate in these 3 sec (in rad)? 3. Through what angle does the wheel rotate between 2 and 3 sec (in rad)? A. 18 A. 5 A. 0 B. 24 B. 10 B. 1 C. 30 C. 15 C. 2 D. 36 D. 20 D. 3 E. 48 E. 25 E. 4
Relation between angular and linear quantities Arc length s: = r s Tangential speed of a point P: r = tv Tangential acceleration of a point P: r = ta Note: This is not the centripetal acceleration ar This is the tangential acceleration at
Black board example 10.2 vt A fly is sitting at the end of a ceiling fan blade. The length of the blade is 0.50 m and it spins with 40.0 rev/min. a) Calculate the (tangential) speed of the fly. b) What are the tangential and angular speeds of another fly sitting half way in? c) Starting from rest it takes the motor 20 seconds to reach this speed. What is the angular acceleration? d) At the final speed, with what force does the fly (m = 0.01 kg, r = 0.50 m) need to hold on, so that it won t fall off? (Note difference between angular and centripetal acceleration).
Torque sin F F r cos F A force F is acting at an angle on a lever that is rotating around a pivot point. r is the distance between the pivot point and F. This force-lever pair results in a torque on the lever = sin r F
Black board example 10.7 i-clicker Two mechanics are trying to open a rusty screw on a ship with a big ol wrench. One pulls at the end of the wrench (r = 1 m) with a force F = 500 N at an angle = 80 ; the other pulls at the middle of wrench with the same force and at an angle = 90 . What is the net torque the two mechanics are applying to the screw? A. 742 Nm B. 750 Nm C. 900 Nm D. 1040 Nm E. 1051 Nm
Extra Slides The following slides are extra slides; unless they also appeared in the previous slides, they are no not needed for exam or MCAT
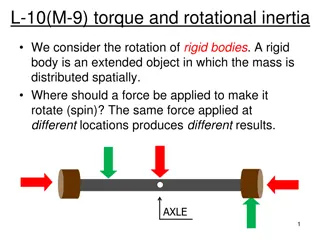
Demo: Both sticks have the same weight. Why is it so much more difficult to rotate the blue stick?
Rotational kinetic energy A rotating object (collection of i points with mass mi) has a rotational kinetic energy of 1 = 2 KR I 2 2 ir I m Where: Moment of inertia or rotational inertia i i
Black board example 10.3 2 i-clicker Four small spheres are mounted on the corners of a weightless frame as shown. 1 3 M = 5 kg; m = 2 kg; 4 a = 1.5 m; b = 1 m a) What is the rotational energy of the system if it is rotated about the z-axis (out of page) with an angular velocity of 5 rad/s b) What is the rotational energy if the system is rotated about the y-axis? i-clicker for question b): A) 281 J B) 291 J C) 331 J D) 491 J E) 582 J
Moment of inertia (rotational inertia) of an object depends on: - the axis about which the object is rotated. - the mass of the object. - the distance between the mass(es) and the axis of rotation. 2 ir I m i i
Calculation of Moments of inertia for continuous extended objects i mi 0 2 2 2 lim = = I r m r dm r dV i i Refer to Table10.2 Note that the moments of inertia are different for different axes of rotation (even for the same object) 1 = I ML 3 1 1 = I MR = I ML 2 12
Moment of inertia for some objects Page 287
Black board example 10.4 Rotational energy earth. The earth has a mass M = 6.0 1024 kg and a radius of R = 6.4 106 m. Its distance from the sun is d = 1.5 1011 m What is the rotational kinetic energy of a) its motion around the sun? b) its rotation about its own axis?
Parallel axis theorem Rotational inertia for a rotation about an axis that is parallel to an axis through the center of mass = CM+ 2 I I Mh I CM h Blackboard example 10.5 What is the rotational energy of a sphere (mass m = 1 kg, radius R = 1m) that is rotating about an axis 0.5 away from the center with = 2 rad/sec?
Conservation of energy (including rotational energy): Again: If there are no non-conservative forces energy is conserved. Rotational kinetic energy must be included in energy considerations! = E E i f + + = + + U K K U K K , , , , i linear initial rotational initial f linear final rotational final
Black board example 10.6 Connected cylinders. Two masses m1 (5.0 kg) and m2 (10 kg) are hanging from a pulley of mass M (3.0 kg) and radius R (0.10 m), as shown. There is no slip between the rope and the pulleys. (a) What will happen when the masses are released? (b) Find the velocity of the masses after they have fallen a distance of 0.5 m. (c) What is the angular velocity of the pulley at that moment?
Torque sin F F r cos F A force F is acting at an angle on a lever that is rotating around a pivot point. r is the distance between the pivot point and F. This force-lever pair results in a torque on the lever = sin r F
Black board example 10.7 i-clicker Two mechanics are trying to open a rusty screw on a ship with a big ol wrench. One pulls at the end of the wrench (r = 1 m) with a force F = 500 N at an angle = 80 ; the other pulls at the middle of wrench with the same force and at an angle = 90 . What is the net torque the two mechanics are applying to the screw? A. 742 Nm B. 750 Nm C. 900 Nm D. 1040 Nm E. 1051 Nm
Torque and angular acceleration Particle of mass m rotating in a circle with radius r. Radial force Fr to keep particle on circular path. Tangential force Ft accelerates particle along tangent. F = ma t t = I Torque acting on particle is proportional to angular acceleration :
= dW F s d Definition of work: = W F s Work in linear motion: = s d F dW Component of force F along displacement s. Angle between F and s. = = cos W F s F s Work in rotational motion: = d dW dW F s d Torque and angular displacement . = = W
Linear motion with constant linear acceleration, a. Rotational motion with constant rotational acceleration, = + = + v v a t t xf xi x f i = + + = + + 1 1 ( ) ( ) x x v v t t f i xi xf f i i f 2 2 1 1 = + + = + + 2 2 x x v t a t t t f i xi x f i i 2 2 2 2 2 2 = + = + 2 ( ) 2 ( ) v v a x x xf xi x f i f i f i
Summary: Angular and linear quantities Linear motion Rotational motion 1 1 = = 2 2 K m v KR I Kinetic Energy: Kinetic Energy: 2 2 = I = F ma Force: Torque: = p mv = I L Momentum: Angular Momentum: = W = W F s Work: Work:
Rolling motion Superposition principle: Rolling motion = Pure translation + Pure rotation Kinetic energy 1 2 1 2 = + 2 2 K Mv I CM CM of rolling motion:
Black board example 10.8 Demo A ring, a disk and a sphere (equal mass and diameter) are rolling down an incline. All three start at the same position; which one will be the fastest at the end of the incline? A. All the same B. The disk C. The ring D. The sphere