Understanding Power System Analysis: Voltage Drop Equations and Phasor Diagrams
Explore the derivation and application of voltage drop equations over transmission lines in power systems, considering inductive and capacitive loads. Learn how to draw phasor diagrams for different scenarios and understand the approximations used to analyze voltage losses.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Exercise 6 Power systems
Question 1 a) Derive the following equation for the voltage drop over a transmission line + cos sin Uloss I R I X b) Can this equation be applied in all situations? c) Draw the phasor diagrams related to the equation in cases where the reactive power is inductive and capacitive.
Question 1 Transmission line is mostly inductive reactance a) Derive the following equation for the voltage drop over a transmission line = + Z R jX = I I jI p q + cos sin Uloss I R I X = U U phase loss b) Can this equation be applied in all situations? c) Draw the phasor diagrams related to the equation in cases where the reactive power is inductive and capacitive.
Question 1 a) Derive the following equation + cos sin Uloss I R I X = I I jI = + Z R jX p q inductive = U U phase loss ) ( ) ( = = = + ; , U U Z I R jX I jI I is active current I is reactive current p q p q phase loss ( ) ( ) 2 = + = + + U RI jRI jIX j XI RI XI j IX RI p q p q p q p q loss longitunal transverse
Question 1 a) Derive the following equation + cos sin Uloss I R I X The voltage drop is typically considered as the difference between the absolute values of the phase voltage (U1,ph U2,ph). A good approximate for this can be attained by projecting the voltage phasor with the larger magnitude onto the smaller voltage phasor. We can approximate that the imaginary part of Uloss is zero (projection onto the smaller voltage phasor with angle of zero). Also, knowing that = = cos , sin I I I I p q ( ) ( ) = + + U RI XI IX j RI We get: p q p q loss 0 + cos sin , U IR IX loss is where the phase angle at the end of the line
Question 1 b) Can this equation be applied in all situations The equation + cos sin Uloss I R I X is only approximate and can be applied in a case with inductive current. For capacity current, q-component is positive: = + I I jI p q The equation in this case is ( loss jX R U + = ) ( ) ( ) ( ) 2 + = + + + = + + I jI RI jRI jIX j XI RI XI j RI IX p q p q p q p q q p
Question 1 c) Draw the phasor diagrams ( ) = + = + + U U IZ U I R jX 1 , 2 , 2 , phase phase phase Inductive load: = I I jI Uphase,1 p q XI XIp Uloss Uphase,2 RI I=Iind Iq RIq XIq Ip RIp j 90 deg. Counter-clockwise = + Z R jX Note: the figure is out of perspective
Question 1 c) Draw the phasor diagrams ( ) = + = + + U U IZ U I R jX 1 , 2 , 2 , phase phase phase Capacitive load: = + I I jI p q XI j 90 deg. Counter-clockwise (in contrast to I) Uphase,1 XIp Ip XIq I=Icap RI Iq RIq Uphase,2 RIp Note: the figure is out of perspective
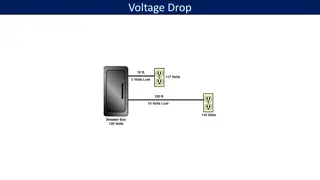
Question 2 Point 2 Point 1 10 MW of active power is transferred using a three-phase line shown in the picture. Line-to-line voltages in the both ends of the line are 110 kV. Calculate the power factor (cos ) of the load.
Question 2 Point 2 Point 1 U U P = 1 X 2 sin 10 MW of active power is transferred using a three-phase line shown in the picture. Line-to-line voltages in the both ends of the line are 110 kV. Calculate the power factor (cos ) of the load. Uph,1 Uph,2 I
Question 2 Phase voltage at point 1 and point 2 X Uphase,2 Uphase,1 = 110 kV, three phases U line B B U U 2 2 P = 1 X 2 Power angle equation for the three phase system sin U U 1 , 2 , line line U U U U 3 3 1 , 2 , phase phase 1 , 2 , line line = = = : 3 sin 3 sin sin Note P X X X The voltage amplitudes are now kept constant with voltage control: Uphase,1 = Uphase,2 The angle difference (power angle) between the voltages is: 110 kV 10 MW 168 PX = = arcsin arcsin . 7 98 110 kV U 1U 2
Question 2 Calculate the power factor of the load. To calculate the power factor of the load, we need to know Pload and Qload. Now, the resistive losses are neglected: P1=P2=Pload=P X P P Q1 Q2 Qload B B Qc/2 2 2 In order to keep the voltage level constant, a certain amount of reactive power has to flow into the line from point 2 and the shunt capacitance Reactive power angle equation for 2 2 U U U the three phase system (between voltage U1 and U2 with a reactance between) and reactive power produced by shunt capacitance (lecture 6): 1 X 2 = cos Q 2 X 2 2 = = Q YU BU c 2 2 Q U U U B 2 2 c 1 X 2 = + = + cos Q Q U 2 load 2 2 X . 4 57 Mvar
S Question 2 Calculate the power factor of the load. Q P load P 10 MW P = = = cos ( ) ( . 4 ) S 2 2 load 2 2 + + P Q 10 MW 57 MVAr load cos . 0 91 inductive , ind since Q 0 load Another way: / / 0 Uphase,2 110 kV . 7 / 98 110 kV U U U . 0 87 mS 110 kV B Uphase,1 X 1 2 2 = = I j j 2 2 3 3 3 168 j 3 jX I Ix c I B x I B Ic 2 2 = 52 6 . A 0 . 4 / 27 6 . A / 90 57 7 . A / 24 5 . I lagging 24.5 degrees to U 2 ( ) = cos cos 24 5 . . 0 91 ind
Question 3 A turbine generator is delivering 20MW at 50Hz to a local load; it is not connected to the grid. The load suddenly drops to 15MW; and the turbine governor starts to close the steam valve after a delay of 0.5s. The stored energy in the rotating parts is 80MJ at 3000rev/min. What is the generated frequency at the end of the 0.5s delay?
Question 3 A turbine generator is delivering 20MW at 50Hz to a local load; it is not connected to the grid. The load suddenly drops to 15MW; and the turbine governor starts to close the steam valve after a delay of 0.5s. The stored energy in the rotating parts is 80MJ at 3000rev/min. What is the generated frequency at the end of the 0.5s delay?
Question 3 What is the generated frequency at the end of the 0.5s delay? Generated steady-state power = 20 MW. Power usage drops to 15 MW. Excess power of 20-15 = 5 MW accelerates the generator (frequency is increased) Rotational energy is thus increased by: 6 = = s 5 . 0 = 5 10 W 5 . 2 MJ Energy P t Rotational energy now: = + = 5 . 2 + = 80 82 5 . MJ E E E 2 1 2 2 E f E f E 1 1 1 2 = = f 2 2 E f 2 1 2 and 2 50 82 5 . = = 50 775 . Hz f 2 80
Question 4 A 625-kVA 2.4 kV generator with X d= 0.20 per unit is connected to a bus through a circuit breaker, as shown in the figure below. Connected through circuit breakers to the same bus are three synchronous motors rated 250 hp, 2.4 kV, 1.0 power factor, 90% efficiency, with X d= 0.20 per unit. The motors are operating at full load, unity power factor, and rated voltage, with the load equally divided among the machines. For interrupting current, presume that transient reactance for the synchronous motors is 1.5 times the subtransient reactance. For the generator, apply the subtransient reactance. (a) Draw the impedance diagram with the impedances marked in per unit on a base of 625 kVA, 2.4 kV. (b) Find the symmetrical short-circuit current in amperes, which must be interrupted by breakers A and B for a three-phase fault at point Q. Simplify the calculations by neglecting the pre-fault current. (c) Repeat part (b) for a three-phase fault at point P.
Circuit breakers typically become active around 100ms after the fault. This equals around 5 cycles (50Hz 20ms per cycle). In this case, we are in a transient state rather than in the substransient state. Question 4 General thoughts breaker http://www.egr.unlv.edu/~eebag/Fault%20Analysis.pdf
Question 4 (a) Draw the impedance diagram marked in per unit on a base of 625kVA, 2.4kV. Base of 625kVA. Motors: Output 250hp, 2.4kV, 1.0 power factor, 90% efficiency. 250 hp W 746 P 9 . 0 hp Motor input: = = = 207 22 . kVA. S cos( ) 1 Motor subtransient reactance: S 625 kVA b = = = ' ' ' ' j 2 . 0 j . 0 603 x X pu , m d m 07.22kVA 2 S 5 . 1 = 5 . 1 = = Motor reactance in transient state: ' ' ' j . 0 603 j . 0 905 x x pu pu m m S=207.22kVA Ub=2.4kV j0.905 Motors Sb=625kVA j0.20 j0.905 R j0.905 GEN Q P
Question 4 b) Let s calculate the transient current in Q using the Thevenin s theorem Any possible fault occurs between the generator and the motors. One phase diagram (one generator, three motors): Zth=? Zg=j0.2 3 of Zm=x m=j0.905 1 1 1 1 = = = 3 . 0 302 Z pu motors Z Z motors m Zth Z Z + j . 0 302 j 2 . 0 motors gen = = = j . 0 1203 Z pu th + j . 0 302 j 2 . 0 Z Z motors gen is Thevenin v oltage voltage at the start of the fault : If Uf 0 . 1 = 0 U pu f U 1 f ' = = = j . 8 315 I pu f j . 0 1203 Z th
Question 4 b Let s calculate the transient current in Q (symmetrical short-circuit current) using the Thevenin s theorem We can calculate the value of base current and absolute value of transient current: Sb=625kVA Ub=2.4kV S 625 B = = = 150 35 . A I B 4 . 2 3 3 U B ' f = = This is current in Fault location Q . 8 315 150 35 . 1250 2 . A I I f Current of breaker A: Im Ig . 0 302 Z + 752A = = = ' j . 8 315 j 0 . 5 motors I I pu g f . 0 502 Z Z g motors Zg=j0.2 Current of breaker B: Zmotors=j0.302 0 . 5 . 8 315 1.105*150.35A=166A = = j . 1 105 Im j pu 3
Question 4 c) b) fault at point P Fault at P: In this case breaker A carries the current fed by generator as in b) Breaker B carries currents of generator and the other two motors B B Im A A Im Ig+2Im Ig Im Im Currents to be interrupted: = = = Breaker A : 0 . 5 I 752 A I I j pu g ( ) = + = + = = Breaker B : 2 0 . 5 j 2 . 1 j 105 . 7 j 21 1084 A I I pu g m