Understanding Moments and Their Effects on Rotation
Moments in physics refer to the tendency of a force to rotate an object about an axis. This content explains how forces can create moments that lead to rotation, the calculation of moments using vectors, clockwise and counterclockwise moments, zero moments, and Varignon's Theorem. Through practical examples, the concepts of moments are illustrated to enhance understanding.
Uploaded on Sep 08, 2024 | 1 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
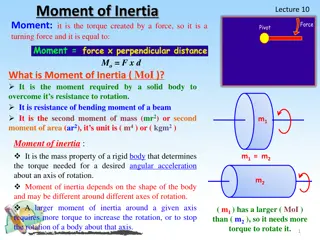
Moment In addition to the tendency to move a body in the direction of its application, a force can also tend to rotate a body about an axis. The axis may be any line which neither intersects nor is parallel to the line of action of the force. M=Fd
Moment about a Point Point of application of a force and line of action of a force are as in Fig: F line of action of a force point of application The magnitude of the moment or tendency of the force to rotate the body about the axis perpendicular to the plane of the body is proportional both to the magnitude of the force and to the moment arm d, which is the perpendicular distance from the axis to the line of action of the force.
Moment: Vector Definition In some two-dimensional and many of the three-dimensional problems to follow, it is convenient to use a vector approach for moment calculations. = = O M r F Position v ector that runs from moment the r F reference point any po to int the line of action of F A r M A d = = = Magnitude of M sin M M rF = = sin M Fr Fd O The : right - identify t to used is rule hand direction. he Direction moment the Thus of about identified be may O-O as a vector F pointing in the direction of thumb, with the fingers curled in the direction of tendency the rotate. to
Clockwise and Counterclockwise moments: If tendency of the force is to rotate its moment arm in a counter clockwise manner it is called counterclockwise moment (CCW). We will assume CCW moment as a positive moment (+). If tendency of the force is to rotate its moment arm in a clockwise manner it is called clockwise moment (CW). We will assume CW moment as a negative moment (-).
Zero moments - If line of action of the force intersects the axis of rotation, there is no moment of the force about this axis of rotation - If line of action of the force is parallel to the axis of rotation, there is no moment of the force about this axis of rotation
Varignons Theorem The moment of a force about any point is equal to the sum of the moments of the components of the force about the same point.
Problems For the figure shown below, find moment of 400 N force about point A using: 1. Scalar approach 2. vector approach. y 3 m O x 450 400 N 6 m A
Scalar Approach y 3 m O x 450 400 N 6 m A = + 0 0 400 = cos 45 6 400 sin 45 3 M A 2545 2 . (Countercl N.m ock wise) M Ans. A
Vector Approach y 3 m (-3,0) O x 450 400 N 6 m (0,-6) A i ) ) i j + = + = 0 0 400 cos 45 ( 400 sin = 45 ( 282 8 . 282 = 8 . F j ) 1 ) 1 ) 0 j 3 j = + + ( ( ( 3 0 ( ( 6 )) 6 r x x i y y j i i 2 2 i j k 0 k = = = 3 6 2545 2 . N.m M r F Ans. A 282 8 . 282 8 . 0
Alternative Solution (Using Varignons Theorem): Assuming that the counterclockwise moment is positive; MB = - Fx.(0.16m) - Fy.(0.2m) where Fx= 400 N and Fy= 693 N MB= -400N(0.16m)-693N(0.2m) = -202.6 N.m We can say MB= -203 N.m Since we assumed that the counterclockwise moment is positive and we obtained a negative moment value, this implies that the direction of MBis actually clockwise. So; the result is exactly the same as before, i.e.