Understanding Map Projections: Types and Applications
Map projection is a systematic transformation of latitudes and longitudes from a curved surface to a flat plane. There are various classifications based on construction methods, tangent surface position, view point of light, and qualities like equal area and equi-distance. Zenithal Polar Equidistance Projection is a mathematical expression for representing Earth's surface on a 2D plane with distortion. Gnomonic Zenithal Polar Projection displays great circles as straight lines with specific characteristics and distortions. Map projections are crucial for creating accurate maps despite inherent distortions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
MAP PROJECTION A map projection is a systematic transformation of the latitudes and longitudes of locations from the surface of a sphere or an ellipsoid into locations on a plane. Projections are a subject of several pure mathematical fields, including differential geometry, projective geometry, and manifolds. However, "map projection" refers specifically to a cartographic projection. Definition: A map projection is a systematic transformation of the latitudes and longitudes of locations from the surface of a sphere or an ellipsoid into locations on a plane. Maps cannot be created without map projections.
CLASSIFICATION OF MAP PROJECTION a) Based on the method of construction: 1) Perspective 2) Non - Perspective b) Based on the method of construction: 1) Conical 2) Cylindrical 3) Zenithal 4) Convectional c) Based on the position of tangent surface: 1) Equatorial 2) Polar 3) Oblique d) Based on the position of view point of light: 1) Gnomonic 2) Stereographic 3)Orthographic e) Based on the qualities: 1) Equal area 2) Equi-distance 3) Orthographic 4)Azimuthal 5)Convectional
ZENITHAL POLAR EQUIDISTANCE PROJECTION Map projection is a mathematical expression using which the three-dimensional surface of earth is represented in a two dimensional plane. The process of projection results in distortion of one or more map properties such as shape, size, area or direction. A single projection system can never account for the correct representation of all map properties for all the regions of the world. Therefore, hundreds of projection systems have been defined for accurate representation of a particular map element for a particular region of the world. The zenithal equidistant and equal-area projections are mathematical derivatives of the orthographic-stereographic-gnomonic family of true projections. In its conventional polar tangency the basic zenithal projection consists of straight meridians radiating from the pole which intersect concentric parallels at right angles. In the zenithal equidistant projection the parallel spacing is modified to show true distance along the meridians (but not in any other direction). The zenithal projections are very good for depicting polar regions (even up to 45o scale distortions are less than about +10%) and in their transverse or oblique forms they are usefully applied in other areas as well.
GOMONIC ZENITHAL POLAR PROJECTION A gnomonic map projection displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. Characteristics: 1. The pole is a point forming the center of the projection and the parallels are concentric circles. 2. The meridians are straight lines radiating from pole having correct angular distance between them. 3. The meridians intersect the parallels at right angles. 4. The parallels are unequally spaced. The distances between the parallels increase rapidly toward the margin of the projection. This causes exaggeration of the scale along the meridians. 5. The scale along the parallels increases away from the center of the projection. 6. The exaggeration and distortion of shapes increases away from the center of the projection. The exaggeration in the meridian scale is greater than that in any other zenithal projection. 7. It is neither equal area nor orthomorphic. 8. An arc on the globe which is a part of a great circle is represented as a straight line on this projection. This is because the radii from the centre of the globe are produced to meet the plane placed tangentially at the pole. 9. It is used to show great-circle paths as straight lines and thus to assist navigators and aviators in determining appropriate courses.
ZENITHAL POLAR EQUAL AREA PROJECTION Such a map projection is called equidistant. Maps are also described as equidistant when the separation between parallels is uniform (e.g., distances along meridians are maintained). No map projection maintains distance proportionality in all directions from any arbitrary point. The zenithal equal-area projection is constructed by adjusting the spacing of parallels of the basic zenithal projection so that they enclose on the map the same area as they do on the globe, thus retaining the property of equivalence. It turns out that shape distortion is also minimal (less than about +10%) within 50o of the pole as well. As in all zenithal projections, directions from the center of this projection are shown correctly as azimuths of great circles. Zenithal projections are not widely used in topographic mapping, however, because the conical do an even better job of portraying small areas.
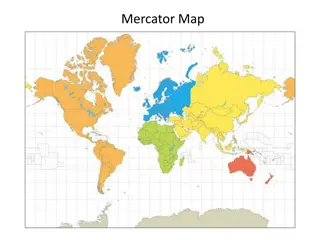
MERCATOR PROJECTION The Mercator projection is a conformal one meaning that angles and direction are preserved within a small area while distance is distorted. On some occasions the cylinder is rotated; transverse and oblique Mercator projections exist. These projections are generally used to represent specific geographic areas. Characteristics: 1.Conformal 2. Parallels unequally spaced, distance increases away from equator 3. Loxodromes or rhumb lines are straight (all straight lines on the map are lines of constant azimuth) 4. The image of the poles are at infinity 5. Used for navigation and regions near equator. Invented in 1569 by Gerardus Mercator graphically 6. Is a cylindrical projection. 7. Has the equator or two symmetrical latitudes serve as lines of contact. 8. Is conformal and represents small shapes well due to angular relationships. 9. Preserves direction and lines represent accurate compass bearings. 10. Preserves scale along equator with increasing area distortion closer to the poles, which cannot be displayed.
CYLINDRICAL EQUAL AREA PROJECTION A cylindrical projection can be imagined in its simplest form as a cylinder that has been wrapped around a globe at the equator. The points on the spherical grid are transferred to the cylinder which is then unfolded into a flat plane. The equator is the "normal aspect" or viewpoint for these projections. This family of projections are typically used to represent the entire world. When projected from the center of the globe with the normal aspect, the typical grid appearance for cylindrical projections shows parallels and meridians forming straight perpendicular lines. The spacing varies depending on the type of cylindrical projection. Characteristics: 1. Meridians are equidistant 2. Lines of latitude and longitude are parallel intersecting at 90 degrees 3. Forms a rectangular map 4. Scale along the equator or standard parallels (lines of tangency) is true 5. Can have the properties of equidistance, conformity or equal area 6. The poles are represented as lines 7. Compromise (general) distortion 8. Both meridians and parallels are equally spaced (equidistant) 9. It can be visualized as a cylinder wrapped around the globe. 10. Once the graticule is projected onto the cylinder, the cylinder is opened to get a grid like pattern of latitudes and longitudes. 11. The longitudes (meridians) and latitudes (parallels) appear as straight lines. 12. Length of equator on the cylinder is equal to the length of the equator therefore is suitable for showing equatorial regions
SIMPLE CONICAL PROJECTION In flattened form a conic projection produces a roughly semicircular map with the area below the apex of the cone at its center. When the central point is either of Earth's poles, parallels appear as concentric arcs and meridians as straight lines radiating from the center. CHARACTERISTICS 1. Lines of latitude and longitude are intersecting at 90 degrees. 2. Meridians are straight lines. 3. Parallels are concentric circular arcs. 4. Scale along the standard parallel(s) is true. 5. Can have the properties of equidistance, conformality or equal area. 6. The pole is represented as an arc or a point. 7. Equally spaced parallels Compromise. 8. It can be visualized as a cone placed on the globe, tangent to it at some parallel. 9.After projecting the graticule on to the cone, the cone is cut along one of the meridian and unfolded. 10. Parallels appear as arcs with a pole and meridians as straight lines that converge to the same point. 11. It can represent only one hemisphere, at a time, northern or southern. 12. Suitable for representing middle latitudes.
CHOICE OF MAP PROJECTION Characteristics of Map Projections Properties Projection Category Common Uses Conformal Preserves local shapes and angles Topographic maps, navigation charts, weather maps Equal Area Preserves areas Dot density maps, thematic maps Equidistant Preserves distance from one or two specified points to all other points on the map Maps of airline distances, seismic maps showing distances from an earthquake epicenter Azimuthal All directions are true from a single specified point (usually the center) to all other points on the map Navigation and route planning maps Compromise No point is completely distortion free; distortion is minimized near the center and along the equator World maps