Understanding Exponential Notation and Evaluating Expressions with Exponents
Learn about the vocabulary related to exponential notation, how to write expressions with exponents, and how to evaluate expressions with exponents both inside and outside parentheses. Practice problems included to enhance understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
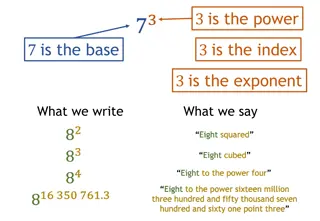
A. Vocabulary: Power Exponent multiplied Base Exponential notation with exponents Power product in which the factors are the same Exponent tells how many times the base is Base the number that is multiplied Exponential notation an expression that is written
B. Writing out an expression with exponential notation: 22 = 2 x 2 35= 3 x 3 x 3 x 3 x 3 n4= n x n x n x n y3= y x y x y 2y3= 2 x y x y x y (the exponent is only connected to the y, so that is the only thing that is expanded)
1. 54 2. b3 3. 2x3 4. 12y4
C. Writing in exponential notation: 7 x 7 x 7 x 7 = 74 n x n x n x n x n x n = n6 3 x m x m = 3m2 2 x y x y x y x y = 2y4
1. 9 x 9 x 9 2. y y y y y 3. 4 x n x n x n x n x n 4. 15 x x x x 5. 10 x b x b x b
Note: You can also evaluate problems that include exponents ex. y4+ 3 for y = 2 24+ 3 2 2 2 2 + 3 16 + 3 = 19 End of Part 1
Up until now, all exponents were connected to only one number/variable, known as the base 2y5 When an expression inside parentheses is raised to a power, everything inside the parentheses becomes the base (2y)5
A. To solve problems with exponents on the outside of the parentheses, you must connect/distribute the exponent to everything on the inside 1. (3a)4 2. (5y)3 53 y3 34 a4 81 a4 125 y3 81a4 125y3
B. You can also do this same thing with evaluating: Example: (4m)3 for m = 2 43 m3 43 23 64 8 512
1. (10y)2 2. (6m)3 3. (8n)5 for n=2 End of Part 2
C. When you have exponents both inside and outside of the parentheses: You must multiply the exponents (52)3 Multiply your exponents 56 = 15,625
1. (84)3 2. (k7)5 3. (3a2)5
A. If you have the same base in the top and bottom of the fraction, and they have exponents, you can simplify B. As long as they are the same base, you will take the top exponent and subtract the bottom exponent 35 33 Take the exponents and subtract 5 3 = 2 32
1. 78 2. b12 b4 x3 3. x 75
C. If you do not have the same base, you cannot subtract the exponents m3 t5 D. If there are multiple bases, combine your like bases and leave the rest where they were x3y2 z4 x6y2 = x3z4 Here are your like bases subtract the exponents
1. 126145 2. a3b8 b2c9 3. 3xy 12y 124