Understanding Exponents and Rules
Exponents are a shortcut for repeated multiplication. Learn how to write expressions using exponents, evaluate expressions containing exponents, and apply rules for dealing with exponents. Explore examples and see how to write expressions in exponential form, evaluate them using calculators, and simplify them. Understand the importance of signs and parentheses when evaluating exponents. Master multiplying powers with the same base and practice expanding expressions into factored and simplified exponential forms.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Exponent Rules Standard: 8.EE.1
Today What are Exponents? How do you write an expression using exponents? How do you evaluate an expression that contains exponents? What RULES do we have for dealing with exponents?
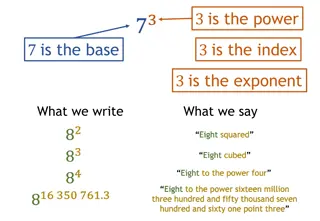
What is an Exponent? Exponents are a short-cut way of writing repeated multiplication.
How do you Write an expression using exponents? Expressions can be written in two different forms. Factored Form Exponential Form 8 8 2 2 2 8 2 5 9 5 5 5 5 9
How do you Evaluate an expression that contains exponents? To find 54 on my calculator I type in: = 625
How do you Evaluate an expression that contains exponents? To find 34 2 on my calculator I type in: = 2,592
Write the expression in Exponential Form. 6 6 3 4 6 3 = 6 3 4 Now, evaluate your expression using the ^ button on your calculator. 7,776
When evaluating exponents you must watch the sign and the parenthesis! 5 = (5 5) 5 = 5 5 = 25 = 25 ( 5) = ( 5) ( 5) = 25
Use your calculator. Be sure to enter the ( ) where indicated. Evaluate. 16 1. ( 4) -16 2. 4 -16 3. (4) 16 4. 4
Multiplying Powers with the Same Base RULE 1
8 8- -37. 37. Complete the table below. Expand each expression into factored form and then rewrite it in a simplified exponential form as shown in the example.
8 8- -37a. 37a. Work with your team to compare the bases and exponents of the original form to the base and exponent of the simplified exponent form. Write a statement to describe the relationships you see. Original Form Simplified Form The base is the same in both forms. 52 5 =5 The simplified exponent can be determined by adding (+) the original exponents together. 2 2 = 26 3 3 = 3
RULE for Multiplying Powers with the Same Base Step 1 Step 2 ADD the Exponents Step 3 Evaluate if needed Keep the Base 52 5 = 5 = 5 or 78,125 2 2 =2 = 26or 64 3 3 = 3 = 3 or 19,683
Step 1 Step 2 ADD the Exponents Step 3 Evaluate if needed Keep the Base 8 8- -37b. 37b. Write the expression in simplified exponential form. Use your new exponent rule! You do not have to evaluate it. 20 = 20 (20 )(20 ) =
8 8- -37c. 37c. One study team rewrote the expression 10 5 as 50 . Is their simplification correct? Explain your reasoning. NO it is not correct. 103 54= 625,000 , while 507= 781,250,000,000 The BASES have to be the SAME! On this one One of the bases is 10 and the other base is 5.
Find SET 1 on your practice sheet. You will have a set amount of time to complete these problems. Then we will review them.
Dividing Powers with the Same Base RULE 2
If you ADD (+) the exponents when multiplyingpowers with the same base . What do you think you are supposed to do when dividing powers with the same base?
RULE for Dividing Powers with the Same Base Step 1 Step 2 Subtract the Exponents Step 3 Evaluate if needed Keep the Base 65 6 = 6 = 6 or 216
Why does subtracting the exponents work? 6 6 6 6 6 6 6 65 62 = = 63
Step 1 Step 2 Subtract the Exponents Step 3 Evaluate if necessary Keep the Base Write the expression in simplified exponential form. Use your new exponent rule! You do not have to evaluate them. 7 7 = 7 = 7 1) ?? ? 2) = 9 = 9 ?? ?? = 2 = 2 3)
Find SET 2 on your practice sheet. You will have a set amount of time to complete these problems. Then we will review them.
Power of a Power RULE 3
8 8- -61. 61. When a number is raised to a power, and then raised to a power again, the result follows a consistent pattern. Complete the table below. Expand each expression into factored form and then rewrite it with new exponents as shown in the example.
8 8- -61a. 61a. Work with your team to describe the pattern between the exponents in the original form and the exponents in the simplified exponential form. Original Form Simplified Form The exponents in the simplified form are the product of the exponent inside the parentheses and the exponent outside the parentheses. (52) =5 (2 ) = 2 (3 ) = 3
RULE for a Power of a Power Step 1 Step 2 Evaluate if needed Multiply the exponent inside the ( ) by the exponent on the outside. (52) =5 =9,765,625 (2 ) = 2 = 256 (3 ) = 3 = 4,782,969
8 8- -61b. 61b. Visualize (20 ) written in factored form. What would it look like? How many 20 s would be written down? the factored form would look like 8 sets of 20 20 20. There would be 24 of the 20 s. Now, write the express (20 ) in simplified exponential form. You do not have to evaluate it. Use your new rule! (20 ) =20
Find SET 3 on your practice sheet. You will have a set amount of time to complete these problems. Then we will review them.
Look at this example of how to find a Power of a Product. (2 3 ) =2 3 Write this in simplified Exponential form. (7 2 ) = 7 2
Find SET 4 on your practice sheet. You will have a set amount of time to complete these problems. Then we will review them.