Understanding Angles: Definitions, Examples, and Postulates
Explore the world of angles with definitions of angle parts, types of angles, angle pairs, Angle Addition Postulate, and more. Dive into examples and classwork exercises to enhance your understanding of angles in geometry.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
1-4: Measuring Angles
Parts of an Angle Formed by the union of two rays with the same endpoint. Called sides of the angle Called the vertex of the angle 3 ways to name BAC or CAB A (Vertex) 1 B Exterior Interior 1 A C
Types of Angles Acute Obtuse Right Straight x x x x x = x = 90 90 180 180 0 90 x x Congruent Angles Angles with the same measure A B A m A = m B B A B
Example 1: , 1, ZXY , X YXZ 1). Name the angle below. Name the sides and the vertex of the angle. , XZ XY X Y 1 X Z 2). Label the 3 points on the figure below so that the angle has sides KQ and KN. Q K N
Protractor Postulate A Consider and a point on one side of . Every ray of the form can be paired one to one with a real number 0 to 180. OB OB OA A O B
45 135 D A a d m AOD Example 2: What is ? m AOD = a d m AOD = 135 45 m AOD = 45 135 m AOD = m AOD = = = 90 90 90 90
Postulate 1-8: Angle Addition Postulate AOC m AOC If point B is in the interior of , then: m AOB m BOC + = B A O C Example 3: If , what are and ? 175 m ABC = 5 4 10 175 x x + + = 10 5 175 x+ = 10 170 x = 17 x = m CBD m ABD m CBD m ABD = = 6(17) 5 6 97 m ABD D A (6x-5) m CBD = = + 4(17) 10 (4x+10) B C 78
1-5: Exploring Angle Pairs
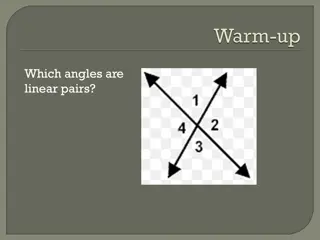
Types of Angle Pairs Adjacent Angles Two coplanar angles with a: _______________, ________________, _______________________________ no common interior points 1 2 common side common vertex 3 4 Vertical Angles 3 1 2 Two angles whose sides are __________ ______ opposite rays 4 B Complementary Angles Two angles whose measures have a sum of _______ 90 43 47 1 2 A Supplementary Angles Two angles whose measures have a sum of _______ 180 4 3
Example 1: Use the diagram below. Is each statement true? Explain. L M P A 74 106 O N a. and are adjacent angles. PAL LAM Yes, they have a common side b. and are vertical angles. PAO NAM No, they don t share two pairs of opposite rays c. and are supplementary. PAO NAO Yes, the sum of the angles is 180
Assumptions About Angles Assumptions you can make: 1. Angles are adjacent 2. Angles are adjacent and supplementary 3. Angles are vertical angles Assumptions you can t make: 1. Angles or segments are congruent 2. An angle is a right angle 3. Angles are complementary
Postulate 1-9: Linear Pair Postulate A Linear Pair of angles are angles that are both supplementary and adjacent. ABC DBC Ex 2 What are the measures of and ? C x+ x 3 19 7 9 + 19 7 + 10 9 180 = 10 180 x+ 10 x = x = 3 x x A B D = m ABC = + = 3(17) 19 70 170 17 m DBC = = 7(17) 9 110
Theorem 2-1: Vertical Angle Theorem Vertical angles are congruent and 1 3 2 1 4 4 2 3 Example 3: What is the value of x? What are the angle measures? 2 42 3 10 x x + = 2 52 3 x x + = 52 x = 2(52) 42 3(52) 10 x+ (2 42) x (3 10) + = = 146 146
Angle Bisector two ray A ________ which divides an angle into ______ _______________ angles. congruent X A Y AY is an angle bisector. Z JLN m JLM = 42 LM Example 4: bisects . If , what is ? 2(42) = m JLN J 84 42 L M N