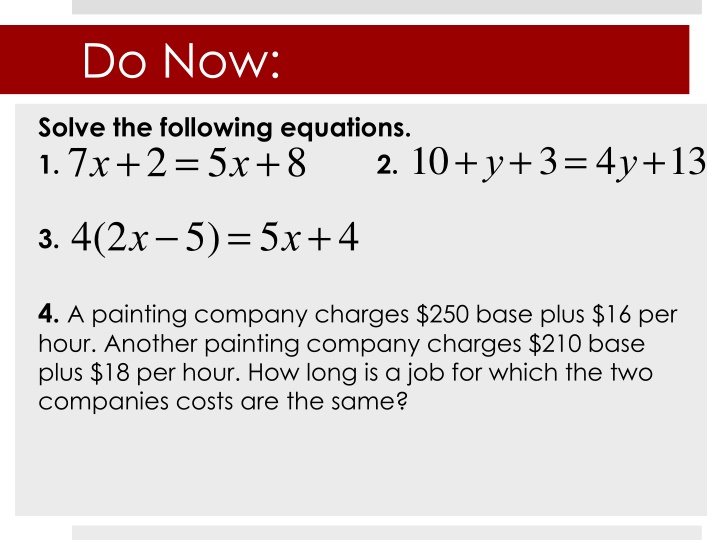Equations and Painting Costs Analysis
In this lesson, students will solve equations involving variables on both sides to determine the number of solutions. Additionally, a comparison is made between two painting companies based on their pricing structures to find the point where their costs are equal. Various examples and concepts related to identities and contradictions in equations are explored, helping students develop their problem-solving skills. The lesson also includes steps for solving multi-step equations and determining solutions for different scenarios.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Do Now: Solve the following equations. 1. 7x+2= 5x+8 4(2x-5)= 5x+4 10+y+3= 4y+13 2. 3. 4. A painting company charges $250 base plus $16 per hour. Another painting company charges $210 base plus $18 per hour. How long is a job for which the two companies costs are the same?
Objective: Students will be able to solve equations to determine the number of solutions.
Lesson 6.2 Equations with Variables on Both Sides Identities and Contradictions Identity When solving an equation, if you get an equation that is always true, the original equation is an identity, and it has infinitely many solutions. 2 + 1 = 2 + 1 3 = 3 WORDS NUMBERS 2 + x = 2 + x ALGEBRA x x 2 = 2
Lesson 6.2 Equations with Variables on Both Sides Identities and Contradictions Contradiction When solving an equation, if you get a false equation, the original equation is a contradiction, and it has no solutions. 1 = 1 + 2 1 = 3 WORDS NUMBERS x = x + 3 ALGEBRA x x 0 = 3
Lesson 6.2 Equations with Variables on Both Sides Let s Review .. Steps on solving Multi-Step Equations Don t call me after midnight 1. D= Distributive property 2. C= combine like term 3. M = move variable to one side 4. A = addition/subtraction 5. M = Multiplication/division
Lesson 6.2 Equations with Variables on Both Sides Example 1: Solve the following equations. Then check your solution. a.) 10-5x+1= 7x+11-12x
Lesson 6.2 Equations with Variables on Both Sides Example 1: Solve the following equations. Then check your solution. b.) 12x-3+x =5x-4+8x
Lesson 6.2 Equations with Variables on Both Sides Example 1: Solve the following equations. Then check your solution. c.) 4y+7 y = 10+3y 2c+7+c= 14+3c+21 d.)
Lesson 6.2 Equations with Variables on Both Sides Example 2: Determine whether the following have one solution, No Solution or infinitely many. If it has one solution, find it. a.) 12q 15= 3(4q +3)
Lesson 6.2 Equations with Variables on Both Sides Example 2: Determine whether the following have one solution, No Solution or infinitely many. If it has one solution, find it. b.) 4(3x+1) 7x = 6+5x 2
Lesson 6.2 Equations with Variables on Both Sides Example 2: Determine whether the following have one solution, No Solution or infinitely many. If it has one solution, find it. c.) 4(-2x+5)= -32x-28 ( )-4 8x+4(4x+3)= 4 6x+4 d.)
Lesson 6.2 Equations with Variables on Both Sides Guided Practice: Determine whether the following have one solution, No Solution or infinitely many. If it has one solution, find it. 1.) 2.) 2(3x + 2) = 6x + 4 8x 3 = 15 + 5x 3.) 4x + 16 = 2x 4.) 7x x + 2 = 8x 8