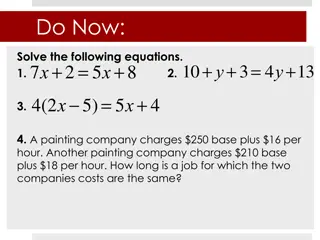Solving Application Problems with Systems of Equations

Learn to set up and solve application problems involving multiple variables using systems of equations. This involves defining variables, writing equations, and step-by-step solutions for scenarios like work schedules, math tests, and inventory management. Practice examples like determining work hours at different pay rates, distributing question types in a test, and allocating inventory quantities based on costs.

• Math Problems
• Systems of Equations
• Application Scenarios
• Variable Definitions
• Problem Solving

ando_a Follow

Uploaded on Feb 20, 2025 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Solving An Application Problems 1. Define variables 2. Write as a system of equations 3. Solve showing all steps 4. State your solution (in words!)

2. Setting Up Application Problems 1. Define variables 2. Write as a system of equations

3. Example 1: Work Schedule You worked 18 hours last week and earned a total of $124 before taxes. Your job as a lifeguard pays $8 per hour, and your job as a cashier pays $6 per hour. How many hours did you work at each job? x = hours as lifeguard x + y = 18 8x + 6y = 124 y = hours as cashier

4. Solve Define variables: 00:30 Percent Complete 100% IRESPOND QUESTION MASTER System of equations: A.) Response A B.) Response B State your solution(s): C.) Response C D.) Response D E.) Response E

5. Example 2: Math Test A math test is to have 20 questions. The test format uses multiple choice worth 5 points each and problem solving worth 6 points each. The test has a total of 100 points. Write a system to determine how many of each type of question are used. x = MC ? s x + y = 20 5x + 6y = 100 y = Problem solving ? s

6. Solve Define variables: 00:30 Percent Complete 100% IRESPOND QUESTION MASTER System of equations: A.) Response A B.) Response B State your solution(s): C.) Response C D.) Response D E.) Response E

7. Example 3: Hair Salon A hair salon receives a shipment of 84 bottles of hair conditioner to use and sell to customers. The two types of conditioners received are Type A, which is used for regular hair, and Type B, which is used for dry hair. Type A costs $6.50 per bottle and Type B costs $8.25 per bottle. The hair salon s invoice for the conditioner is $588. How many of each type are in the shipment? x = # Type A bottles x + y = 84 y = # Type B bottles 6.5x + 8.25y = 588

8. Solve Define variables: 00:30 Percent Complete 100% IRESPOND QUESTION MASTER System of equations: A.) Response A B.) Response B State your solution(s): C.) Response C D.) Response D E.) Response E

9. Example 4 : Solve - Ticket Sales You sell tickets for admission to your school play and collect a total of $104. Admission prices are $6 for adults and $4 for children. You sold 21 tickets. How many adult tickets and how many children tickets did you sell? x + y = 21 10 adult tickets and 11 children tickets 6x + 4y = 104

10. Solve Define variables: 00:30 Percent Complete 100% IRESPOND QUESTION MASTER System of equations: A.) Response A B.) Response B State your solution(s): C.) Response C D.) Response D E.) Response E

11. Example 5 : Solve Pizza Hut Casey orders 3 pizzas and 2 orders of breadsticks for a total of $29.50. Rachel orders 2 pizzas and 3 orders of breadsticks for a total of $23. How much does pizza cost? 3x + 2y = 29.50 2x + 3y = 23 $8.50 for pizza

12. Solve Define variables: 00:30 Percent Complete 100% IRESPOND QUESTION MASTER System of equations: A.) Response A B.) Response B State your solution(s): C.) Response C D.) Response D E.) Response E

13. Closing Chickens and Pigs A farmer saw some chickens and pigs in a field. He counted 60 heads and 176 legs. Find out exactly how many chickens and how many pigs he saw.

14. Warm up Solve the given system by substitution: ( ) 1) y = 2x 7 2, 3 3x + 3y = - 3 Solve the given system by elimination: ( ) 0, 1 2) -3x + 4y = -4 3x 6y = 6

15. What is the Best Method for the following? 1 2 2 1. y = 4x 3 5x 2y = 6 = + 3. 3 y x = 2 y x 2. 4x 5y = 13 2x + 5y = 5

16. What is the Best Method for the following? 2 3 x = 5. 3x 2y = 6 y = 2x 4 4. 2 y x = + 3 y 6. x + y = 4 2x + 3y = 7