Quadratic Equations and Applications in Real Life

Explore various quadratic equations and their applications through graphing, solving, and real-world scenarios. Topics include finding zeros, solving word problems, analyzing football height trajectory, determining plot areas, and calculating horizon distances. Discover the relationship between quadratic equations and their graphs, and delve into practical problem-solving methods using math.

• Quadratic Equations
• Real Life Applications
• Graphing Calculator
• Problem Solving
• Mathematics

kat_sil Follow

Uploaded on Sep 09, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

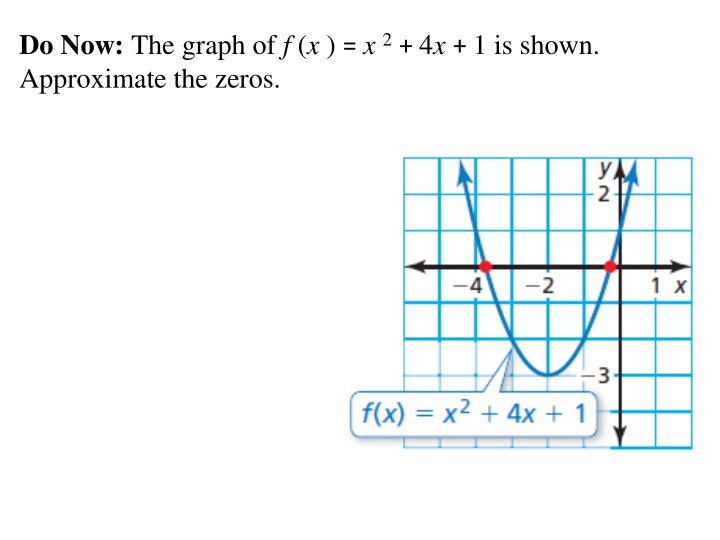
1. Do Now: The graph of f (x ) = x 2+ 4x + 1 is shown. Approximate the zeros.

2. Word Problems

3. Solve using the graphing calculator -2x2 2= 4x

4. Solve using the graphing calculator 1) x2 x 2 = 0 3) x2+ 7x = -10 3) x2+ x = 12

5. A football player kicks a football 2 feet above the ground with an initial vertical velocity of 75 feet per second. The function h = 16t 2+ 75t + 2 represents the height h (in feet) of the football after t seconds. (a) Find the height of the football each second after it is kicked. (b) Use the results of part (a) to estimate when the height of the football is 50 feet. (c) Using a graph, after how many seconds is the football 50 feet above the ground?

6. A farmer plants a rectangular pumpkin patch in the northeast corner of a square plot of land. The area of the pumpkin patch is 600 square meters. What is the area of the square plot of land?

7. The distance d (in miles) that you can see to the horizon with your eye level h feet above the water is given by the equation written below. How far can you see when your eye level is 5 feet above the water? 3h d = 2

8. Closing: When a quadratic equation has two solutions, what do you know about the graph of its related function? One solution? No solution?

9. Homework: None