Equations of Motion in Normal and Tangential Coordinates
Equations of motion can be expressed in terms of normal, tangential, and binormal directions. The normal and tangential components play crucial roles in describing the motion of an object. Through scalar equations and component representations, these equations help analyze forces and acceleration in a coordinate system. Explore the detailed approach in solving problems related to TNB (Tangential-Normal-Binormal) systems in the provided classroom practice examples.
Uploaded on Sep 27, 2024 | 2 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
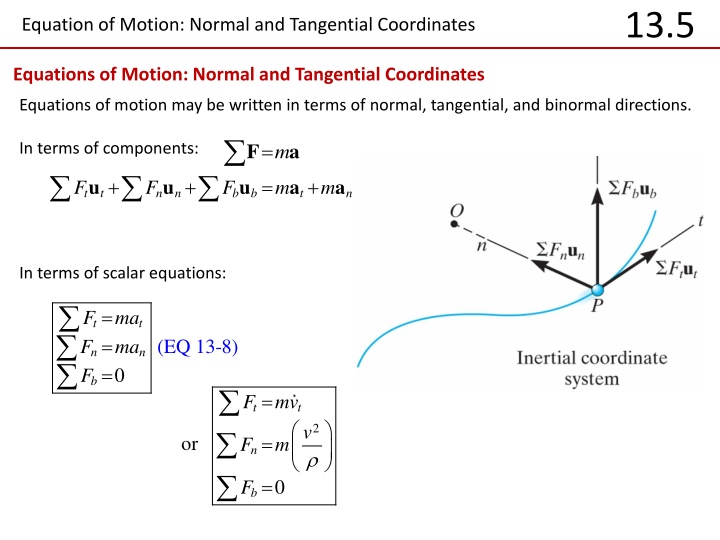
13.5 Equation of Motion: Normal and Tangential Coordinates Equations of Motion: Normal and Tangential Coordinates Equations of motion may be written in terms of normal, tangential, and binormal directions. F F u = a m In terms of components: + + = + u u a a F F m m t t n n b b t n In terms of scalar equations: = = = F F F ma ma t t (EQ 13-8) n n 0 b = F mv t t v 2 = or F m n = 0 F b
In-Class Practice Problem 1 Wait .is this a TNB problem? Confirm the coordinate system as drawn FBD of a passenger
In-Class Practice Problem 2 Wait .is this a TNB problem? Awesome? Or Lame? Coilovers don t go between a-arms https://www.youtube.com/watch?v=ntygfUZFxu8 FBD of a passenger
In-Class Practice Problem 3 https://www.youtube.com/watch?v=T8FOc9RSAUU