Regression Lines and Predictions
In this lesson, learn how to make predictions using regression lines, interpret residuals, and understand the importance of a regression line in data analysis. Explore the calculation and interpretation of a residual, the slope and y-intercept of a regression line, and how to determine the equation of a least-squares regression line. Discover the process of calculating the least squares regression line and using a graphing calculator to find specific values. Understand the significance of a regression line in modeling the relationship between quantitative variables and making accurate predictions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
LESSON 3.2 PREDICTIONS, RESIDUALS, AND INTERPRETING A REGRESSION LINE
OBJECTIVES Make predictions using regression lines, keeping in mind the dangers of extrapolation. Calculate and interpret a residual. Interpret the slope and y intercept of a regression line. Determine the equation of a least-squares regression line using technology or computer output.
TO CALCULATE THE LEAST SQUARES REGRESSION LINE Follow the exact steps to find your correlation (r- value) with one more step Enter all data into L1 and L2 Stat- Calc - LinReg(a+bx) But BEFORE you hit enter a second time . After LinReg(a+bx) comes on your screen we must enter L1,L2,Y1 after it and then hit enter To get to L1- 2nd1 To get to L2 2nd2 To get to Y1 VARS-Y-VARS-Function Y1 Zoom #9
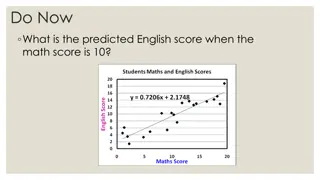
You can also use your graphing calculator to find a specific value Hit 2ndTRACE Enter for value Enter the x value you are looking for into x= Hit enter
REGRESSION LINE When the relationship between two quantitative variables is linear, we can use a regression line to model the relationship and make predictions A regression line is a line that describes how a response variable y changes as an explanatory variable x changes.
LINEAR REGRESSION EQUATION ? = ? + ?? ? = y-hat means predicted y ? = y-intercept ? = slope
RESIDUAL A residual is the difference between an actual value of y and the value of y predicted by the regression line. That is,
TO INTERPRET A RESIDUAL The actual y-context was residual higher/lower than the predicted for x = # Fill in the underlines with your data from the problem
EXTRAPOLATION The prediction we make using the regression line is called an extrapolation Extrapolation is the use of a regression line for prediction far outside the interval of x values used to obtain the line. Such predictions are often not accurate.
Y-INTERCEPT When we use 0 rubberbands the predicted distance traveled is 25.33
Y-INTERCEPT When x = 0 context, the predicted y- context is y-intercept. Fill in the underlines with your data from the problem
SLOPE When we add 1 rubberband, the predicted distance traveled increases by 7.464cm.
SLOPE With each additional x-context, the predicted y-context increases/decreases by slope. Fill in the underlines with your data from the problem