MO Diagrams for Boron Trifluoride
M
O
D
i
a
g
r
a
m
s
f
o
r
M
o
r
e
C
o
m
p
l
e
x
M
o
l
e
c
u
l
e
s
Chapter 5
Wednesday, October 14, 2015
B
o
r
o
n
t
r
i
f
l
u
o
r
i
d
e
1
.
P
o
i
n
t
g
r
o
u
p
D
3
h
2
.
3
.
M
a
k
e
r
e
d
u
c
i
b
l
e
r
e
p
s
f
o
r
o
u
t
e
r
a
t
o
m
s
4
.
G
e
t
g
r
o
u
p
o
r
b
i
t
a
l
s
y
m
m
e
t
r
i
e
s
b
y
r
e
d
u
c
i
n
g
e
a
c
h
Γ
Γ
2
s
=
A
1
’
+
E
’
Γ
2
p
z
=
A
2
’
’
+
E
’
’
Γ
2
p
x
=
A
2
’
+
E
’
Γ
2
p
y
=
A
1
’
+
E
’
x
y
z
x
y
z
x
y
z
B
o
r
o
n
t
r
i
f
l
u
o
r
i
d
e
Γ
2
s
=
A
1
’
+
E
’
Γ
2
p
z
=
A
2
’
’
+
E
’
’
Γ
2
p
x
=
A
2
’
+
E
’
Γ
2
p
y
=
A
1
’
+
E
’
W
h
a
t
i
s
t
h
e
s
h
a
p
e
o
f
t
h
e
g
r
o
u
p
o
r
b
i
t
a
l
s
?
2
s
:
A
1
’
E
’
(
y
)
?
?
E
’
(
x
)
T
h
e
p
r
o
j
e
c
t
i
o
n
o
p
e
r
a
t
o
r
m
e
t
h
o
d
p
r
o
v
i
d
e
s
a
s
y
s
t
e
m
a
t
i
c
w
a
y
t
o
f
i
n
d
h
o
w
t
h
e
A
O
s
s
h
o
u
l
d
b
e
c
o
m
b
i
n
e
d
t
o
g
i
v
e
t
h
e
r
i
g
h
t
g
r
o
u
p
o
r
b
i
t
a
l
s
(
S
A
L
C
s
)
.
Which combinations of the
three AOs are correct?
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
A
1
’
=
F
a
+
F
b
+
F
c
+
F
a
+
F
c
+
F
b
+
F
a
+
F
b
+
F
c
+
F
a
+
F
c
+
F
b
F
a
I
n
t
h
e
p
r
o
j
e
c
t
i
o
n
o
p
e
r
a
t
o
r
m
e
t
h
o
d
,
w
e
p
i
c
k
o
n
e
A
O
i
n
e
a
c
h
s
e
t
o
f
i
d
e
n
t
i
c
a
l
A
O
s
a
n
d
d
e
t
e
r
m
i
n
e
h
o
w
i
t
t
r
a
n
s
f
o
r
m
s
u
n
d
e
r
e
a
c
h
s
y
m
m
e
t
r
y
o
p
e
r
a
t
i
o
n
o
f
t
h
e
p
o
i
n
t
g
r
o
u
p
.
F
b
F
c
T
h
e
g
r
o
u
p
o
r
b
i
t
a
l
w
a
v
e
f
u
n
c
t
i
o
n
s
a
r
e
d
e
t
e
r
m
i
n
e
d
b
y
m
u
l
t
i
p
l
y
i
n
g
t
h
e
p
r
o
j
e
c
t
i
o
n
t
a
b
l
e
v
a
l
u
e
s
b
y
t
h
e
c
h
a
r
a
c
t
e
r
s
o
f
e
a
c
h
i
r
r
e
d
u
c
i
b
l
e
r
e
p
r
e
s
e
n
t
a
t
i
o
n
a
n
d
s
u
m
m
i
n
g
t
h
e
r
e
s
u
l
t
s
.
A
1
’
=
4
F
a
+
4
F
b
+
4
F
c
A
1
’
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
A
2
’
=
F
a
+
F
b
+
F
c
–
F
a
–
F
c
–
F
b
+
F
a
+
F
b
+
F
c
–
F
a
–
F
c
–
F
b
F
a
I
n
t
h
e
p
r
o
j
e
c
t
i
o
n
o
p
e
r
a
t
o
r
m
e
t
h
o
d
,
w
e
p
i
c
k
o
n
e
A
O
i
n
e
a
c
h
s
e
t
o
f
i
d
e
n
t
i
c
a
l
A
O
s
a
n
d
d
e
t
e
r
m
i
n
e
h
o
w
i
t
t
r
a
n
s
f
o
r
m
s
u
n
d
e
r
e
a
c
h
s
y
m
m
e
t
r
y
o
p
e
r
a
t
i
o
n
o
f
t
h
e
p
o
i
n
t
g
r
o
u
p
.
F
b
F
c
T
h
e
g
r
o
u
p
o
r
b
i
t
a
l
w
a
v
e
f
u
n
c
t
i
o
n
s
a
r
e
d
e
t
e
r
m
i
n
e
d
b
y
m
u
l
t
i
p
l
y
i
n
g
t
h
e
p
r
o
j
e
c
t
i
o
n
t
a
b
l
e
v
a
l
u
e
s
b
y
t
h
e
c
h
a
r
a
c
t
e
r
s
o
f
e
a
c
h
i
r
r
e
d
u
c
i
b
l
e
r
e
p
r
e
s
e
n
t
a
t
i
o
n
a
n
d
s
u
m
m
i
n
g
t
h
e
r
e
s
u
l
t
s
.
A
2
’
=
0
There is no
A
2
’ group orbital!
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
E
’
=
2
F
a
–
F
b
–
F
c
+
0
+
0
+
0
+
2
F
a
–
F
b
–
F
c
+
0
+
0
+
0
F
a
I
n
t
h
e
p
r
o
j
e
c
t
i
o
n
o
p
e
r
a
t
o
r
m
e
t
h
o
d
,
w
e
p
i
c
k
o
n
e
A
O
i
n
e
a
c
h
s
e
t
o
f
i
d
e
n
t
i
c
a
l
A
O
s
a
n
d
d
e
t
e
r
m
i
n
e
h
o
w
i
t
t
r
a
n
s
f
o
r
m
s
u
n
d
e
r
e
a
c
h
s
y
m
m
e
t
r
y
o
p
e
r
a
t
i
o
n
o
f
t
h
e
p
o
i
n
t
g
r
o
u
p
.
F
b
F
c
T
h
e
g
r
o
u
p
o
r
b
i
t
a
l
w
a
v
e
f
u
n
c
t
i
o
n
s
a
r
e
d
e
t
e
r
m
i
n
e
d
b
y
m
u
l
t
i
p
l
y
i
n
g
t
h
e
p
r
o
j
e
c
t
i
o
n
t
a
b
l
e
v
a
l
u
e
s
b
y
t
h
e
c
h
a
r
a
c
t
e
r
s
o
f
e
a
c
h
i
r
r
e
d
u
c
i
b
l
e
r
e
p
r
e
s
e
n
t
a
t
i
o
n
a
n
d
s
u
m
m
i
n
g
t
h
e
r
e
s
u
l
t
s
.
E
’
=
4
F
a
–
2
F
b
–
2
F
c
E
’
(
y
)
Γ
2
s
=
A
1
’
+
E
’
Γ
2
p
z
=
A
2
’
’
+
E
’
’
Γ
2
p
x
=
A
2
’
+
E
’
Γ
2
p
y
=
A
1
’
+
E
’
W
h
a
t
i
s
t
h
e
s
h
a
p
e
o
f
t
h
e
g
r
o
u
p
o
r
b
i
t
a
l
s
?
2
s
:
A
1
’
E
’
(
y
)
?
?
E
’
(
x
)
W
e
c
a
n
g
e
t
t
h
e
t
h
i
r
d
g
r
o
u
p
o
r
b
i
t
a
l
,
E
’
(
x
)
,
b
y
u
s
i
n
g
n
o
r
m
a
l
i
z
a
t
i
o
n
.
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
Normalization condition
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
nine terms, but the six
overlap (
S
) terms are zero.
A
1
’ wavefunction
Normalization condition for group orbitals
So the normalized
A
1
’ GO is:
L
e
t
’
s
n
o
r
m
a
l
i
z
e
t
h
e
A
1
’
g
r
o
u
p
o
r
b
i
t
a
l
:
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
nine terms, but the six
overlap (
S
) terms are zero.
E’
(
y
) wavefunction
So the normalized
E’
(
y
) GO is:
N
o
w
l
e
t
’
s
n
o
r
m
a
l
i
z
e
t
h
e
E
’
(
y
)
g
r
o
u
p
o
r
b
i
t
a
l
:
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
So the normalized
E
’(
x
) GO is:
Γ
2
s
=
A
1
’
+
E
’
Γ
2
p
z
=
A
2
’
’
+
E
’
’
Γ
2
p
x
=
A
2
’
+
E
’
Γ
2
p
y
=
A
1
’
+
E
’
W
h
a
t
i
s
t
h
e
s
h
a
p
e
o
f
t
h
e
g
r
o
u
p
o
r
b
i
t
a
l
s
?
2
s
:
A
1
’
E
’
(
y
)
?
E
’
(
x
)
N
o
w
w
e
h
a
v
e
t
h
e
s
y
m
m
e
t
r
i
e
s
a
n
d
w
a
v
e
f
u
n
c
t
i
o
n
s
o
f
t
h
e
2
s
G
O
s
.
B
F
3
-
P
r
o
j
e
c
t
i
o
n
O
p
e
r
a
t
o
r
M
e
t
h
o
d
W
e
c
o
u
l
d
d
o
t
h
e
s
a
m
e
a
n
a
l
y
s
i
s
t
o
g
e
t
t
h
e
G
O
s
f
o
r
t
h
e
p
x
,
p
y
,
a
n
d
p
z
o
r
b
i
t
a
l
s
(
s
e
e
n
e
x
t
s
l
i
d
e
)
.
notice the GOs are
orthogonal (
S =
0).
The content explores MO diagrams for Boron Trifluoride, focusing on point group transformation, reducible reps for outer atoms, and group orbital symmetries. The Projection Operator Method is utilized to determine the shape of group orbitals and how atomic orbitals combine to form the correct group orbitals.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
MO Diagrams for More Complex Molecules Chapter 5 Wednesday, October 14, 2015
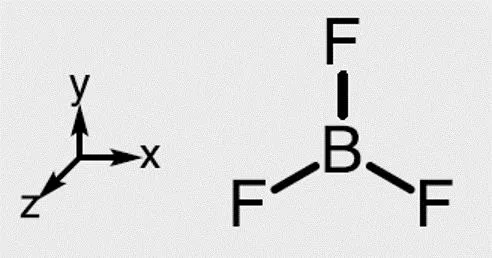
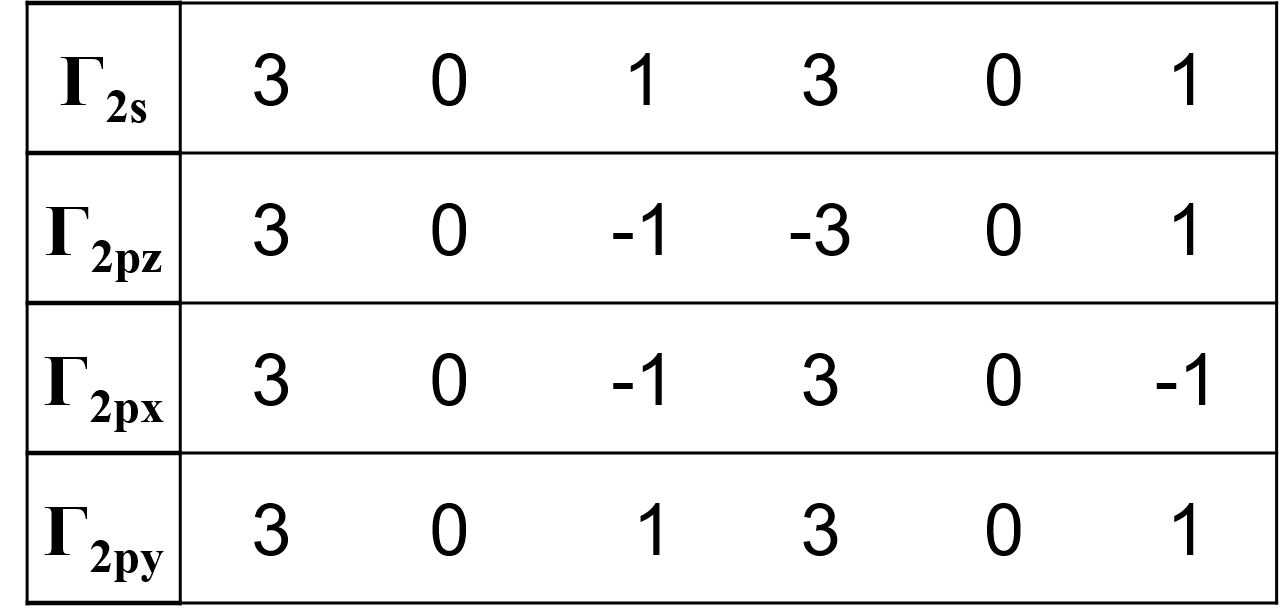
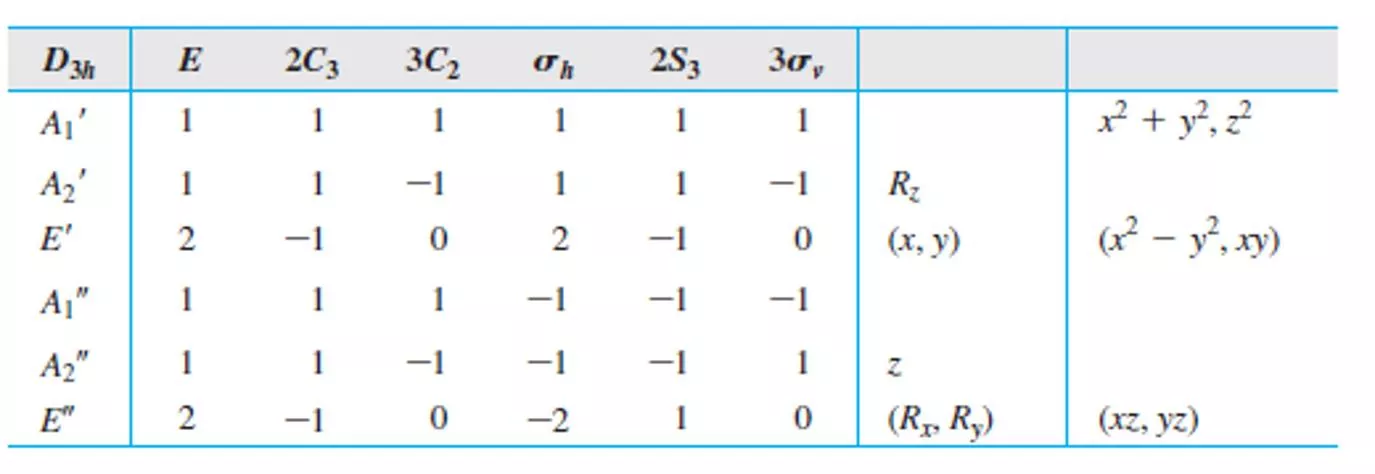
Boron trifluoride 1. Point group D3h 3. Make reducible reps for outer atoms z 2. x y x z y y z x 3 0 1 3 0 1 2s 3 0 -1 -3 0 1 2pz 3 0 -1 3 0 -1 2px 3 0 1 3 0 1 2py 4. Get group orbital symmetries by reducing each 2s = A1 + E 2pz = A2 + E 2px = A2 + E 2py = A1 + E
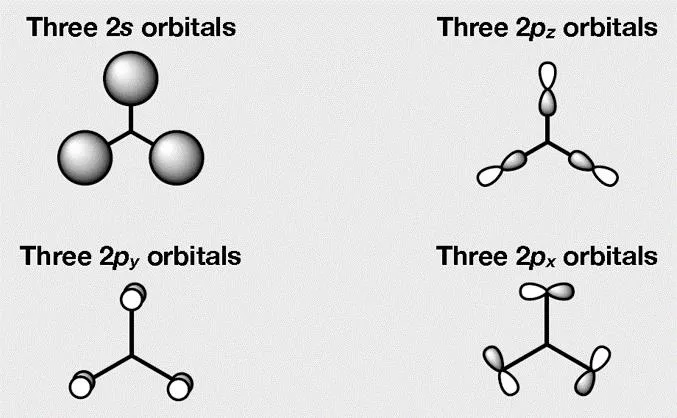
Boron trifluoride 2s = A1 + E 2pz = A2 + E 2px = A2 + E 2py = A1 + E What is the shape of the group orbitals? ? ? 2s: A1 E (y) E (x) Which combinations of the three AOs are correct? The projection operator method provides a systematic way to find how the AOs should be combined to give the right group orbitals (SALCs).
BF3 - Projection Operator Method In the projection operator method, we pick one AO in each set of identical AOs and determine how it transforms under each symmetry operation of the point group. Fa E C3 C32C2(a)C2(b)C2(c) S3 S32 v(a) AO h v(b) v(c) Fa Fa Fb Fc Fa Fc Fb Fa Fb Fc Fa Fc Fb Fb Fc 1 1 1 1 1 1 1 1 1 1 1 1 A1 A1 = Fa + Fb + Fc + Fa + Fc + Fb + Fa + Fb + Fc + Fa + Fc + Fb A1 = 4Fa + 4Fb + 4Fc A1 The group orbital wavefunctions are determined by multiplying the projection table values by the characters of each irreducible representation and summing the results.
BF3 - Projection Operator Method In the projection operator method, we pick one AO in each set of identical AOs and determine how it transforms under each symmetry operation of the point group. Fa E C3 C32C2(a)C2(b)C2(c) S3 S32 v(a) AO h v(b) v(c) Fa Fa Fb Fc Fa Fc Fb Fa Fb Fc Fa Fc Fb Fb Fc 1 1 1 -1 -1 -1 1 1 1 -1 -1 -1 A2 A2 = Fa + Fb + Fc Fa Fc Fb + Fa + Fb + Fc Fa Fc Fb A2 = 0 There is no A2 group orbital! The group orbital wavefunctions are determined by multiplying the projection table values by the characters of each irreducible representation and summing the results.
BF3 - Projection Operator Method In the projection operator method, we pick one AO in each set of identical AOs and determine how it transforms under each symmetry operation of the point group. Fa E C3 C32C2(a)C2(b)C2(c) S3 S32 v(a) AO h v(b) v(c) Fa Fa Fb Fc Fa Fc Fb Fa Fb Fc Fa Fc Fb Fb Fc 0 0 0 2 0 0 0 2 -1 -1 -1 -1 E E = 2Fa Fb Fc + 0 + 0 + 0 + 2Fa Fb Fc + 0 + 0 + 0 E = 4Fa 2Fb 2Fc E (y) The group orbital wavefunctions are determined by multiplying the projection table values by the characters of each irreducible representation and summing the results.
BF3 - Projection Operator Method 2s = A1 + E 2pz = A2 + E 2px = A2 + E 2py = A1 + E What is the shape of the group orbitals? ? ? 2s: A1 E (y) E (x) We can get the third group orbital, E (x), by using normalization. ?2?? = 1 Normalization condition
BF3 - Projection Operator Method Let s normalize the A1 group orbital: A1 wavefunction ??1 = ?a[?(2?Fa) + ?(2?Fb) + ?(2?Fc)] Normalization condition for group orbitals ?2?? = 1 nine terms, but the six overlap (S) terms are zero. 2 [?(2?Fa) + ?(2?Fb) + ?(2?Fc)]2?? = 1 ?a 2 ?2(2?Fa)?? + ?2(2?Fb)?? + ?2(2?Fc)?? = 1 ?a 1 21 + 1 + 1 = 1 ?a= ?a 3 1 So the normalized A1 GO is: ??1 = 3[?(2?Fa) + ?(2?Fb) + ?(2?Fc)]
BF3 - Projection Operator Method Now let s normalize the E (y) group orbital: E (y) wavefunction ?? (?)= ?a[2?(2?Fa) ?(2?Fb) ?(2?Fc)] nine terms, but the six overlap (S) terms are zero. 2 [2?(2?Fa) ?(2?Fb) ?(2?Fc)]2?? = 1 ?a 24 ?2(2?Fa)?? + ?2(2?Fb)?? + ?2(2?Fc)?? = 1 ?a 1 24 + 1 + 1 = 1 ?a ?a= 6 1 So the normalized E (y) GO is: ?? (?)= 6[2?(2?Fa) ?(2?Fb) ?(2?Fc)]
BF3 - Projection Operator Method 1 ??1 = 3[?(2?Fa) + ?(2?Fb) + ?(2?Fc)] 1 ?? (?)= 6[2?(2?Fa) ?(2?Fb) ?(2?Fc)] ? ?? the probability of finding an electron in ?? in a group orbital, ?= ? for a normalized group orbital. ?? so ?? 1 So the normalized E (x) GO is: ?? (?)= 2[?(2?Fb) ?(2?Fc)]
BF3 - Projection Operator Method 2s = A1 + E 2pz = A2 + E 2px = A2 + E 2py = A1 + E What is the shape of the group orbitals? notice the GOs are orthogonal (S = 0). ? 2s: A1 E (y) E (x) Now we have the symmetries and wavefunctions of the 2s GOs. We could do the same analysis to get the GOs for the px, py, and pz orbitals (see next slide).
