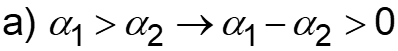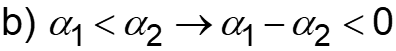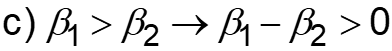Maximizing Selectivity and Yield in Chemical Reactions
Review: Multiple Rxns & Selectivity
2) Series rxns
3) Complex rxns
1) Parallel / competing rxns
Maximize selectivity / yield to maximize production of desired product
Review: Maximizing S
D/U
for
Parallel Rxns
What reactor conditions and
configuration maximize selectivity?
a) If E
D
> E
U
Specific rate of desired reaction k
D
increases:
Use higher temperature
b) If E
D
< E
U
less rapidly with increasing T
Use lower temperature(not so low
that the reaction rate is tiny)
more rapidly with increasing T
To favor production of the desired product
Now evaluate concentration:
→
Use large C
A
→
Use small C
A
→
Use large C
B
→
Use small C
B
High C
B
favors
desired
product
formation
High C
B
favors
undesired
product
formation
(
keep C
B
low
)
High C
A
favors desired
product formation
High C
A
favors
undesired
product formation
(
keep C
A
low
)
The reactor V (for a given
0
) and
that maximizes C
B
occurs when dC
B
/dt=0
so
opt
Review: Reactions in Series: C
j
& Yield
(desired)
(undesired)
Time
is the key factor here!!!
Spacetime
for a flow reactor
Real time t
for a batch reactor
To maximize the production of D, optimize the time (batch) or spacetime (flow)
L10: Nonelementary Reaction Kinetics
•
Nonelementary reaction kinetics: no direct correspondence between
reaction order and stoichiometry
–
Nonelementary kinetics
–
Pseudo-steady-state hypothesis (PSSH)
–
Chain reactions: cracking ethane or polymerizations
–
Enzymatic reactions (covered in CHBE 471)
–
Bioreactors (covered in CHBE 471)
In practice, knowledge of the reaction mechanism helps use to design better
catalyst, trouble shoot, aid in troubleshooting poor reactor performance
•
Rate law is typically determined from experimental data
•
Goal: Use the experimental rate law to postulate a reaction mechanism
•
Elementary
: the reaction orders and stoichiometric coefficients are
identical
Review (L4): Reversible Reactions
K
C
: concentration equilibrium constant (capital K)
A
t
e
q
u
i
l
i
b
r
i
u
m
,
t
h
e
r
e
a
c
t
i
o
n
r
a
t
e
i
s
z
e
r
o
,
r
A
=
0
Rate of disappearance of A (forward rxn):
Rate of generation of A (reverse reaction):
Thermodynamic equilibrium relationship
consumed
generated
Determining Mechanism to Describe
Nonelementary Reaction Kinetics
•
If the reaction were elementary, the reaction kinetics would follow:
•
Instead experiments show that the kinetics are:
•
N
o
n
e
l
e
m
e
n
t
a
r
y
k
i
n
e
t
i
c
s
a
r
e
t
h
e
r
e
s
u
l
t
o
f
m
u
l
t
i
p
l
e
e
l
e
m
e
n
t
a
r
y
r
e
a
c
t
i
o
n
s
t
e
p
s
a
n
d
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
s
(
a
n
i
n
t
e
r
m
e
d
i
a
t
e
t
h
a
t
i
s
s
o
r
e
a
c
t
i
v
e
i
t
i
s
c
o
n
s
u
m
e
d
a
s
f
a
s
t
a
s
i
t
i
s
f
o
r
m
e
d
)
N
o
n
e
l
e
m
e
n
t
a
r
y
How do we determine the mechanism?
•
Postulate a reaction mechanism that is
a series of elementary reactions
•
Derive a rate equation for the postulated mechanism
•
Is the rate equation for the postulated mechanism consistent with the
experimental results?
For example…
Postulating a Reaction Mechanism
1.
I
f
C
B
a
p
p
e
a
r
s
i
n
t
h
e
d
e
n
o
m
i
n
a
t
o
r
o
f
t
h
e
r
a
t
e
l
a
w
,
t
h
e
n
o
n
e
e
l
e
m
e
n
t
a
r
y
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
A
*
is a reactive intermediate
2.
I
f
t
h
e
d
e
n
o
m
i
n
a
t
o
r
c
o
n
t
a
i
n
s
a
c
o
n
s
t
a
n
t
t
h
a
t
i
s
n
o
t
m
u
l
t
i
p
l
i
e
d
b
y
a
c
o
n
c
e
n
t
r
a
t
i
o
n
,
t
h
e
n
o
n
e
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
3.
I
f
t
h
e
n
u
m
e
r
a
t
o
r
c
o
n
t
a
i
n
s
a
s
p
e
c
i
e
s
c
o
n
c
e
n
t
r
a
t
i
o
n
,
t
h
e
n
o
n
e
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
Apply:
C
N
O
i
n
d
e
n
o
m
i
n
a
t
o
r
:
NO collides with reactive intermediate, NO
3
C
N
O
&
C
O
2
i
n
n
u
m
e
r
a
t
o
r
:
NO and O
2
produce NO
3
in one reaction step
C
o
n
s
t
a
n
t
i
n
d
e
n
o
m
i
n
a
t
o
r
:
NO
3
produces NO and O
2
(reverse of previous?)
A Reaction Mechanism for
Observed Kinetics?
Apply:
C
NO
in denominator:
C
NO
& C
O2
in numerator:
Constant in numerator:
Postulated mechanism:
Does this add up to
the overall reaction?
+
Now derive a rate equation for the postulated mechanism and check if
it describes the experimentally observed rate equation
Postulated Mechanism for
Nonelementary Reaction Kinetics
Nonelementary kinetics, result of
multiple elementary rxns & active
intermediates
Postulated mechanism:
•
-r
NO
is in terms of C
NO3
, which is not measurable species because it is a
reactive intermediate
(so reactive it is consumed as fast as it is formed)
•
Need to get C
NO3
in terms of measurable species and plug into -r
NO
Consumption of NO:
(change signs)
Write –r
NO
for the postulated reaction mechanism
Pseudo-Steady State Hypothesis
Postulated mechanism
Reactive intermediate,
must replace C
NO3
in
the rate equation
1)
Write
r
NO3
2)
Rearrange to get
C
NO3
in terms of measurable species
3)
plug eq for
C
NO3
back into -r
NO
C
NO3
is very small, and NO
3
is assumed to be so reactive that it is consumed
as fast as it is formed, so
P
s
e
u
d
o
-
S
t
e
a
d
y
S
t
a
t
e
H
y
p
o
t
h
e
s
i
s
:
N
e
t
f
o
r
m
a
t
i
o
n
o
f
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
≈
0
Factor out to simplify
Concentration of Reactive Intermediate
Postulated mechanism
Reactive
intermediate
Now we will rearrange and simplify to see if it matches the experimental data
Observed rate equation
(nonelementary)
P
l
u
g
C
N
O
3
i
n
t
o
-
r
N
O
Solve for
C
NO3
in
terms of other species
Rearranging the Postulated Rate Eq.
Plug in C
NO3
Factor out
Common
denominator
Add fraction
Multiply
Postulated mechanism
Reactive
intermediate
Comparison Between Postulated
and Experimental Rate Equation
Compare rate eq for postulated mechanism to the experimental rate eq
Postulated mechanism
Reactive
intermediate
Rate equation for
postulated mechanism
Experimentally observed
rate equation
Clicker Q: Are these rate equations the same?
a)
Yes
b)
No
Y
e
s
,
t
h
e
s
e
a
r
e
t
h
e
s
a
m
e
→
p
o
s
t
u
l
a
t
e
d
r
a
t
e
l
a
w
e
x
p
l
a
i
n
s
t
h
e
e
x
p
e
r
i
m
e
n
t
a
l
d
a
t
a
Chain Reaction
•
A chain reaction consists of the following sequence:
–
Initiation
•
formation of an active intermediate (
radicals
)
–
Propagation or chain transfer
•
interaction of an active intermediate with the
reactant or product to produce another active
intermediate (
a radical species
)
–
Termination
•
deactivation of the active intermediate
Common in radical polymerizations and cracking of ethane
Free Radical Polymerizations (4 steps)
monomer
polymer
1
.
I
n
i
t
i
a
t
i
o
n
:
2
.
P
r
o
p
a
g
a
t
i
o
n
:
3
.
C
h
a
i
n
t
r
a
n
s
f
e
r
:
4
a
.
T
e
r
m
i
n
a
t
i
o
n
b
y
a
d
d
i
t
i
o
n
:
Initiator (I) decomposes to 2 free radicals
Chain elongation, new
monomers add to chain
“Live” polymer chain transfers radical to monomer.
Polymer chain is no longer reactive (dead). Can also
transfer to solvent or other species
4
b
.
T
e
r
m
i
n
a
t
i
o
n
b
y
d
i
s
p
r
o
p
o
r
t
i
o
n
a
t
i
o
n
:
PSSH Applied to Thermal Cracking
of Ethane
The thermal decomposition of ethane to
ethylene
, methane, butane and
hydrogen is believed to proceed in the following sequence:
I
n
i
t
i
a
t
i
o
n
:
P
r
o
p
a
g
a
t
i
o
n
:
T
e
r
m
i
n
a
t
i
o
n
:
(
a
)
U
s
e
t
h
e
P
S
S
H
t
o
d
e
r
i
v
e
a
r
a
t
e
l
a
w
f
o
r
t
h
e
r
a
t
e
o
f
f
o
r
m
a
t
i
o
n
o
f
e
t
h
y
l
e
n
e
(
b
)
C
o
m
p
a
r
e
t
h
e
P
S
S
H
s
o
l
u
t
i
o
n
i
n
P
a
r
t
(
a
)
t
o
t
h
a
t
o
b
t
a
i
n
e
d
b
y
s
o
l
v
i
n
g
t
h
e
c
o
m
p
l
e
t
e
s
e
t
o
f
O
D
E
m
o
l
e
b
a
l
a
n
c
e
The rate of formation of ethylene
T
h
e
n
e
t
r
a
t
e
s
o
f
r
e
a
c
t
i
o
n
o
f
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
s
C
2
H
5
•
,
C
H
3
•
,
H
•
a
r
e
:
Goal: replace
C
C2H5•
C
2
H
5
•
w
a
s
f
o
r
m
e
d
i
n
r
x
n
s
2
&
4
,
a
n
d
c
o
n
s
u
m
e
d
i
n
r
x
n
s
3
&
5
:
C
H
3
•
w
a
s
f
o
r
m
e
d
i
n
r
x
n
1
a
n
d
c
o
n
s
u
m
e
d
i
n
r
x
n
2
:
H
•
w
a
s
f
o
r
m
e
d
i
n
r
x
n
3
a
n
d
c
o
n
s
u
m
e
d
i
n
r
x
n
4
:
P
l
u
g
r
a
t
e
e
q
s
i
n
t
o
e
q
a
b
o
v
e
,
a
s
s
u
m
e
r
a
t
e
=
0
(
P
S
S
H
)
&
s
o
l
v
e
f
o
r
r
e
a
c
t
i
v
e
s
p
e
c
i
e
s
Need to replace
C
CH3•
and
C
H•
D
o
t
h
e
s
a
m
e
f
o
r
C
H
•
The rate of formation of ethylene
The net rates of reaction of active intermediates C
2
H
5
•, CH
3
•, H• are (PSSH):
Goal: replace
C
C2H5•
C
2
H
5
• was formed in rxns 2 & 4, and consumed in
rxns 3 & 5:
CH
3
• was formed in rxn 1 and consumed in rxn 2:
H• was formed in rxn 3 and consumed in rxn 4:
Plug rate eqs into eq above, assume rate=0 (PSSH) & solve for reactive species
Plug in expressions for
C
CH3•
and C
H•
into
C
2
H
5
•
rate eq for
C
2
H
5
•
& solve for
C
2
H
5
•
assuming rate = 0 (PSSH)
The rate of formation of ethylene
The net rates of reaction of active intermediates C
2
H
5
•, CH
3
•, H• are (PSSH):
Goal: replace
C
C2H5•
C
2
H
5
• was formed in rxns 2 & 4, and consumed in
rxns 3 & 5:
CH
3
• was formed in rxn 1 and consumed in rxn 2:
H• was formed in rxn 3 and consumed in rxn 4:
Plug rate eqs into eq above, assume rate=0 (PSSH) & solve for reactive species
The rate of formation of ethylene
The net rates of reaction of active intermediates C
2
H
5
•, CH
3
•, H• are (PSSH):
Goal: replace
C
C2H5•
C
2
H
5
• was formed in rxns 2 & 4, and consumed in
rxns 3 & 5:
CH
3
• was formed in rxn 1 and consumed in rxn 2:
H• was formed in rxn 3 and consumed in rxn 4:
Plug expressions for
reactive species into eq
for r
C2H4
above
T
h
e
C
C
2
H
4
d
e
p
e
n
d
s
o
n
C
C
2
H
6
.
H
o
w
d
o
e
s
C
C
2
H
6
c
h
a
n
g
e
w
i
t
h
t
i
m
e
?
N
e
e
d
t
o
e
l
i
m
i
n
a
t
e
t
h
e
r
e
a
c
t
i
v
e
s
p
e
c
i
e
s
Rate of disappearance
of ethane:
The net rates of reaction of active intermediates
CH
3
•
,
C
2
H
5
•,
H•
are (PSSH):
Purpose: replace [CH
3
•] and [H•]
From the previous slide:
F
o
r
a
c
o
n
s
t
a
n
t
-
v
o
l
u
m
e
b
a
t
c
h
r
e
a
c
t
o
r
:
F
o
r
g
i
v
e
n
i
n
i
t
i
a
l
c
o
n
c
e
n
t
r
a
t
i
o
n
o
f
C
2
H
6
a
n
d
t
e
m
p
e
r
a
t
u
r
e
,
t
h
e
s
e
t
w
o
e
q
u
a
t
i
o
n
c
a
n
b
e
s
o
l
v
e
d
s
i
m
u
l
t
a
n
e
o
u
s
l
y
(
i
.
e
.
,
u
s
e
P
o
l
y
m
a
t
h
)
Providing the concentration - time relationship using the PSSH
Other methods can also be used - solve the complete set of ODE mole balances
1.
Mole balances:
C
2
H
6
CH
3
•
CH
4
C
2
H
5
•
C
2
H
4
2.
Rate laws for each species:
(
Batch)
H
2
H•
C
4
H
10
All these O.D.Es can be
solved simultaneously
The comparisons of the results
obtained from the two methods are
shown on page 391 of textbook.
T
h
e
t
w
o
r
e
s
u
l
t
s
a
r
e
i
d
e
n
t
i
c
a
l
,
i
n
d
i
c
a
t
i
n
g
t
h
e
v
a
l
i
d
i
t
y
o
f
t
h
e
P
S
S
H
u
n
d
e
r
t
h
e
s
e
c
o
n
d
i
t
i
o
n
s
Ozone (O
3
) Example Problem
When ozone decomposes in the presence of an inert gas, M, the
following kinetics are observed:
Postulate a reaction mechanism that is consistent with this rate law
This is provided as an extra example that can be skipped if
there isn’t enough time to cover it in class.
S
i
n
c
e
o
n
e
o
x
y
g
e
n
a
t
o
m
i
s
l
o
s
t
f
r
o
m
t
h
e
o
z
o
n
e
m
o
l
e
c
u
l
e
(
O
3
)
,
o
x
y
g
e
n
r
a
d
i
c
a
l
s
(
O
•
)
a
r
e
l
i
k
e
l
y
t
h
e
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
:
Postulating Mechanism for O
3
Decomposition (Step 1)
1.
I
f
C
B
a
p
p
e
a
r
s
i
n
t
h
e
d
e
n
o
m
i
n
a
t
o
r
o
f
t
h
e
r
a
t
e
l
a
w
,
t
h
e
n
o
n
e
e
l
e
m
e
n
t
a
r
y
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
2.
I
f
t
h
e
d
e
n
o
m
i
n
a
t
o
r
c
o
n
t
a
i
n
s
a
c
o
n
s
t
a
n
t
t
e
r
m
,
t
h
e
n
o
n
e
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
3.
I
f
t
h
e
n
u
m
e
r
a
t
o
r
c
o
n
t
a
i
n
s
a
s
p
e
c
i
e
s
c
o
n
c
e
n
t
r
a
t
i
o
n
,
t
h
e
n
o
n
e
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
Apply:
C
O
2
,
C
M
&
C
O
3
i
n
d
e
n
o
m
i
n
a
t
o
r
,
s
o
O
2
,
M
,
a
n
d
O
3
m
u
s
t
e
a
c
h
c
o
l
l
i
d
e
a
w
i
t
h
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
.
W
h
a
t
i
s
t
h
e
r
e
a
c
t
i
v
e
i
n
t
e
r
m
e
d
i
a
t
e
?
C
M
i
s
m
u
l
t
i
p
l
i
e
d
b
y
C
O
2
i
n
t
h
e
d
e
n
o
m
i
n
a
t
o
r
,
s
o
c
o
m
b
i
n
e
P
R
3
w
i
t
h
P
R
1
Postulating Mechanism for O
3
Decomposition (Step 1 continued)
1.
If C
B
appears in the denominator of the rate law, then one elementary rxn
step is probably:
Apply:
C
O2
, C
M
& C
O3
in denominator;
they must collide with reactive intermediate
O
•
W
a
i
t
,
M
i
s
i
n
e
r
t
,
s
o
i
t
c
a
n
n
o
t
r
e
a
c
t
w
i
t
h
O
•
t
o
c
r
e
a
t
e
a
n
e
w
c
h
e
m
i
c
a
l
s
p
e
c
i
e
s
•
A
n
i
n
e
r
t
m
o
l
e
c
u
l
e
c
a
n
p
r
o
v
i
d
e
k
i
n
e
t
i
c
e
n
e
r
g
y
i
n
a
n
o
t
h
e
r
r
e
a
c
t
i
o
n
→
M
m
u
s
t
p
a
r
t
i
c
i
p
a
t
e
i
n
o
n
e
o
f
t
h
e
o
t
h
e
r
r
e
a
c
t
i
o
n
s
W
h
i
c
h
o
n
e
?
Postulating Mechanism for O
3
Decomposition (Steps 2 & 3)
1.
If C
B
appears in the denominator of the rate law, then one elementary rxn
step is probably:
2.
I
f
t
h
e
d
e
n
o
m
i
n
a
t
o
r
c
o
n
t
a
i
n
s
a
c
o
n
s
t
a
n
t
t
e
r
m
,
t
h
e
n
o
n
e
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
3.
I
f
t
h
e
n
u
m
e
r
a
t
o
r
c
o
n
t
a
i
n
s
a
s
p
e
c
i
e
s
c
o
n
c
e
n
t
r
a
t
i
o
n
,
t
h
e
n
o
n
e
r
x
n
s
t
e
p
i
s
p
r
o
b
a
b
l
y
:
Apply:
D
e
n
o
m
i
n
a
t
o
r
d
o
e
s
n
’
t
c
o
n
t
a
i
n
a
c
o
n
s
t
a
n
t
,
s
o
s
t
e
p
2
i
s
n
’
t
i
n
o
u
r
m
e
c
h
a
n
i
s
m
B
o
t
h
C
O
3
a
n
d
C
M
a
p
p
e
a
r
i
n
t
h
e
n
u
m
e
r
a
t
o
r
,
s
o
o
n
e
r
e
a
c
t
i
o
n
s
t
e
p
m
a
y
b
e
:
Note that PR4 is the reverse of PR1
Postulated Mechanism for
Ozone Decomposition
Apply:
C
M
and C
O2
in denominator:
C
O3
in denominator:
C
O3
and C
M
in numerator:
Postulated mechanism:
Does this add up to
the overall reaction?
+
Now derive a rate equation for the postulated mechanism and check if
it describes the experimentally observed rate equation
Postulated Mechanism for
Nonelementary Reaction Kinetics
Nonelementary kinetics, result of
multiple elementary rxns & active
intermediates
Postulated mechanism:
•
-r
O3
is in terms of C
O
•
, which is not measurable species because it is a
reactive intermediate
(so reactive it is consumed as fast as it is formed)
•
Need to get C
O
•
in terms of measurable species and plug into –r
O3
Write –r
O3
for the postulated reaction mechanism
Pseudo-Steady State Hypothesis
Postulated mechanism:
Reactive intermediate,
must replace C
O
•
in the
rate equation
1)
Write
r
O
•
2)
Rearrange to get
C
O
•
in terms of measurable species
3)
plug eq for
C
O
•
back into –r
O3
C
O
•
is very small, and O
•
is so reactive that it is consumed as fast as it is
formed, so apply
pseudo-steady state hypothesis:
Factor out to simplify
Concentration of Reactive O
•
Postulated mechanism:
Now we will rearrange and simplify to see if it matches the experimental data
Observed rate equation
(nonelementary)
P
l
u
g
C
O
•
i
n
t
o
–
r
O
3
Solve for
C
O
•
in terms
of other species
Reactive intermediate,
must replace C
O
•
in the
rate equation
Rearranging the Postulated Rate Eq.
Plug in C
O
•
Multiply out
brackets
Get common
denominator
Postulated mechanism:
Reactive intermediate,
must replace C
O
•
in the
rate equation
Conventional to
remove constant
from 1
st
term
Comparison Between Postulated
and Experimental Rate Equation
Compare
rate eq for postulated mechanism
to the
experimental rate eq
Rate equation for
postulated mechanism
Experimentally observed
rate equation
T
h
e
s
e
a
r
e
t
h
e
s
a
m
e
→
p
o
s
t
u
l
a
t
e
d
r
a
t
e
l
a
w
e
x
p
l
a
i
n
s
t
h
e
e
x
p
e
r
i
m
e
n
t
a
l
d
a
t
a
Postulated mechanism:
Reactive intermediate,
cannot appear in the
rate equation
Factors affecting selectivity and yield in chemical reactions is crucial for optimizing production processes. Explore the concepts of parallel, series, and complex reactions, as well as reactor conditions that influence selectivity. Learn how to maximize desired product formation by manipulating reaction rates, concentrations, and reactor configurations.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
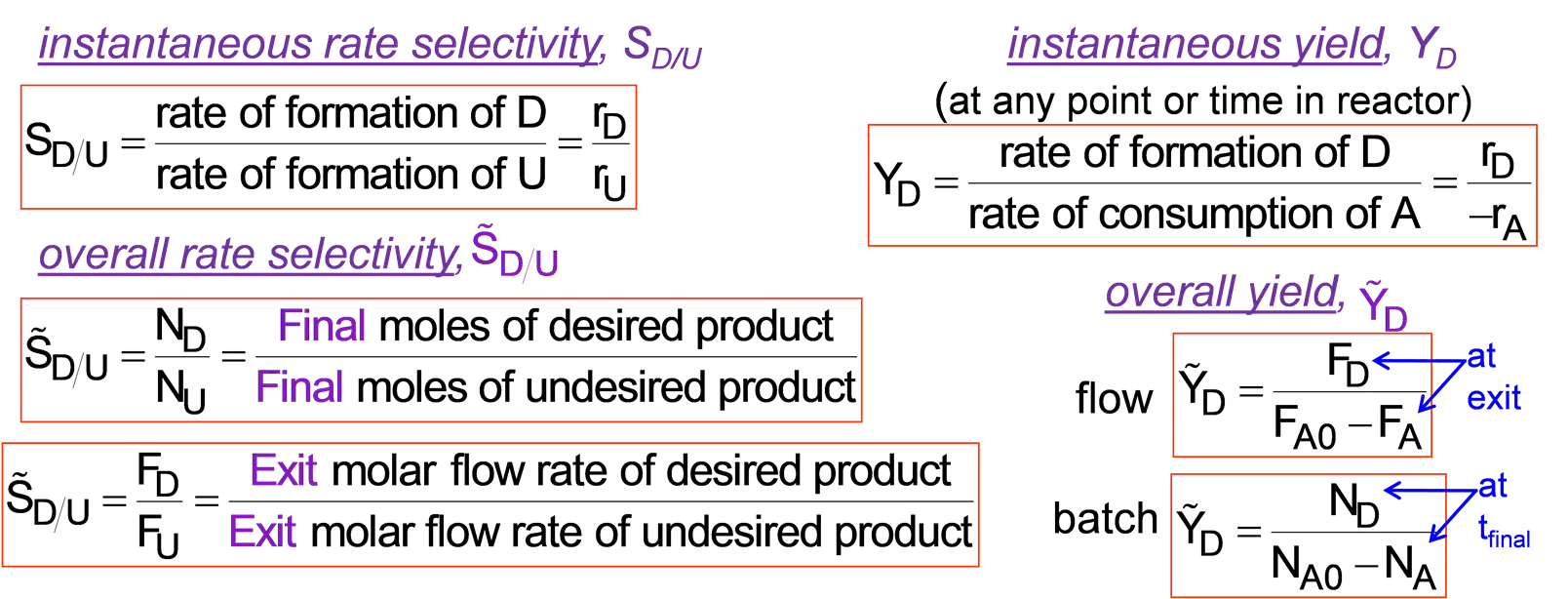
L10-1 Review: Multiple Rxns & Selectivity 1) Parallel / competing rxns k1 k2 2) Series rxns A C B B k1 Desired product A k1 k2 3) Complex rxns A+B C+D A+C E k2 C instantaneous rate selectivity, SD/U rate of formation of D S rate of formation of U instantaneous yield, YD (at any point or time in reactor) D r r = = D r r rate of formation of D rate of consumption of A D U = = Y U D A S overall rate selectivity, D U overall yield, Y N N D Fi nal nal moles of desired product moles of undes D = = D U S F at exit D = Fi ir ed pr od ct u Y flow U D F F A0 A F F Exit E x molar flow rate of desired product molar flow rate of undesir D at tfinal = = D U S N batch D = Y it ed pr oduct D U N N A0 A Maximize selectivity / yield to maximize production of desired product Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Review: Maximizing SD/U for Parallel Rxns ( ) ( A B U A Specific rate of desired reaction kD increases: L10-2 E E D RT U What reactor conditions and configuration maximize selectivity? ) A D 1 2 1 2 = D U S e C C a) If ED > EU b) If ED < EU more rapidly with increasing T less rapidly with increasing T Use lower temperature(not so low that the reaction rate is tiny) Use higher temperature To favor production of the desired product Now evaluate concentration: a) 0 b) 0 1 2 1 2 1 2 1 2 Use large CA Use small CA c) 0 d) 0 1 2 1 2 1 2 1 2 Use large CB Use small CB Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
kD L10-3 D High CA favors undesired product formation (keep CA low) High CA favors desired product formation A+B kU U PFR/PBR Side streams feed low CA Semi-batch reactor slowly feed A to large amt of B CA CSTRs in series Batch reactor High CB favors desired product formation CA When CA & CB are low (end time or position), all rxns will be slow High CB PFR/PBR CA CA High P for gas-phase rxn, do not add inert gas (dilutes reactants) CA 0 CB CA0 0 CB0 0 CSTR PFR/PBR w/ side streams feeding low CB CB Semi-batch reactor, slowly feed B to large amount of A CB CSTRs in series High CB favors undesired product formation (keep CB low) High CA PFR/PBR w/ high recycle PFR/PBR CB CB Dilute feed with inerts that are easily separated from product Low P if gas phase Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign. B consumed before leaving CSTRn
L10-4 Review: Reactions in Series: Cj & Yield Time is the key factor here!!! Spacetime for a flow reactor Real time t for a batch reactor k1 k2 A U D (desired) (undesired) To maximize the production of D, optimize the time (batch) or spacetime (flow) k1 = C C e B A A0 C A 1 k k 2 e e k = C 1 A0 k C B k 2 1 = C C C C C A0 A B opt The reactor V (for a given 0) and that maximizes CB occurs when dCB/dt=0 ( 1 2 1 d k k V ) 1 A0 k C dC k k B 1 2 = k e + = k e 0 2 k k 1 = 1 = 0 opt V = so ln opt opt k k 0 1 2 2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-5 L10: Nonelementary Reaction Kinetics In practice, knowledge of the reaction mechanism helps use to design better catalyst, trouble shoot, aid in troubleshooting poor reactor performance Rate law is typically determined from experimental data Goal: Use the experimental rate law to postulate a reaction mechanism Elementary: the reaction orders and stoichiometric coefficients are identical Nonelementary reaction kinetics: no direct correspondence between reaction order and stoichiometry Nonelementary kinetics Pseudo-steady-state hypothesis (PSSH) Chain reactions: cracking ethane or polymerizations Enzymatic reactions (covered in CHBE 471) Bioreactors (covered in CHBE 471) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-6 Review (L4): Reversible Reactions kA kA Rate of disappearance of A (forward rxn): + + aA b B c C d D a A b B a A b B = k C C = fA r k C C fA r A A c C D C C d = Rate of generation of A (reverse reaction): bA r r + k A = = A,net r r fA r A a A bA b B c C D C C d k C C = consumed generated + r k A A A At equilibrium, the reaction rate is zero, rA=0 a A b B c C D C C d = k C C = + r 0 k A A A a A b B c C D C C d = k C C k A A c C D a A C C d Thermodynamic equilibrium relationship C C k k A = = K C b B KC: concentration equilibrium constant (capital K) A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-7 Determining Mechanism to Describe Nonelementary Reaction Kinetics Overall Reaction: 2NO If the reaction were elementary, the reaction kinetics would follow: r k C = + O 2NO 2 2 2 C NO 1 O NO 2 Instead experiments show that the kinetics are: 2 i NO kC 1 k C + C O Nonelementary 2 NO r = ii NO Nonelementary kinetics are the result of multiple elementary reaction steps and reactive intermediates (an intermediate that is so reactive it is consumed as fast as it is formed) How do we determine the mechanism? Postulate a reaction mechanism that is a series of elementary reactions Derive a rate equation for the postulated mechanism Is the rate equation for the postulated mechanism consistent with the experimental results? For example Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-8 Postulating a Reaction Mechanism 1. If CB appears in the denominator of the rate law, then one elementary rxn step is probably: * B A Collision products + 2. If the denominator contains a constant that is not multiplied by a concentration, then one rxn step is probably: * A Decomposition products 3. If the numerator contains a species concentration, then one step is probably: species C other species? + 2 i NO O NO ii NO 1 k C + overall reaction : 2NO CNO in denominator: NO collides with reactive intermediate, NO3 A* is a reactive intermediate * + A other products? kC C Experimentally observed rate equation for Apply: 2 = r ( ) + O 2NO 2 2 + NO NO 2NO 3 2 CNO & CO2 in numerator: NO and O2 produce NO3 in one reaction step + NO O NO 2 3 Constant in denominator:NO3 produces NO and O2 (reverse of previous?) + NO NO O 3 2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-9 A Reaction Mechanism for Observed Kinetics? 2 i NO O NO ii NO 1 k C + overall reaction : 2NO kC C Experimentally observed rate equation for Apply: 2 = r ( ) + O 2NO 2 2 + + NO NO 2NO CNO in denominator: CNO & CO2 in numerator: Constant in numerator: 3 2 Reactive intermediate NO NO O NO O + 2 3 NO 3 2 k1 k1 k2 + NO O NO Postulated mechanism: 2 3 Does this add up to the overall reaction? + + NO NO 2NO 3 2 + 2NO O 2NO yes 2 2 Now derive a rate equation for the postulated mechanism and check if it describes the experimentally observed rate equation Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-10 Postulated Mechanism for Nonelementary Reaction Kinetics 2 i NO O NO ii NO 1 k C + intermediates Nonelementary kinetics, result of multiple elementary rxns & active kC C 2 = r Reactive intermediate k 1 + Postulated mechanism: NO O NO 2 3 k k 1 2 + NO NO 2NO 3 2 Write rNO for the postulated reaction mechanism ( ) ( ) = NO r rxns that form NO - rxns that consume NO = NO r 1 NO k C 1 NO O k C C 2 NO k C C NO 3 k C 2 k C 3 = + NO r C 2 NO k C C Consumption of NO: (change signs) 1 NO O 1 NO NO 2 3 3 -rNO is in terms of CNO3, which is not measurable species because it is a reactive intermediate (so reactive it is consumed as fast as it is formed) Need to get CNO3 in terms of measurable species and plug into -rNO Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-11 Pseudo-Steady State Hypothesis Postulated mechanism 2 1.) NO O + k Reactive intermediate, must replace CNO3 in the rate equation 1 NO 3 k C k ( + 2 1 k + 2 2.) NO k NO + 3 C 2NO C 3 2 = NO r 1 NO O k C C C Factor out to simplify ) 3 NO 1 k C 1 NO 2 NO k C NO 2 3 = NO r k C 1 NO O 2 NO Write rNO3 Rearrange to get CNO3 in terms of measurable species plug eq for CNO3 back into -rNO = 2 3 NO 1 NO O 1 CNO3 is very small, and NO3 is assumed to be so reactive that it is consumed as fast as it is formed, so NO3 Pseudo-Steady State Hypothesis: Net formation of reactive intermediate 0 = = 2 3 1 NO O NO 1) 2) 3) r k C C k C k 2 N C C NO O N O 3 3 r 0 r 0 k C C k C k C C 1 NO 2 NO NO 3 3 Solve for concentration of reactive intermediate NO3 in terms of other species Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-12 Concentration of Reactive Intermediate + Reactive intermediate k 1 1.) NO O NO Postulated mechanism 2 3 k 1 k + 2 2.) NO NO 2NO 3 2 2 i NO kC 1 k C + C Observed rate equation (nonelementary) O 2 NO r = ii NO ( ) = + NO r 1 NO k C C k C k C O 2 NO 1 NO 2 3 Solve for CNO3 in terms of other species = = NO r 0 1 NO O k C C k C k C C 1 NO 2 NO NO 3 2 3 3 ( ) + = + = k C k C C 1 NO O k C C C k 2 N k C k C C 1 NO 2 NO NO NO 1 O 1 N O O 3 3 2 3 2 1 NO k C k C O 2 = C Plug CNO3 into -rNO NO + 2 NO k C 3 1 1 NO k k C C O ( ) 2 = + NO r 1 NO k C C 2 NO k C k O 1 + 2 N k C 2 1 O Now we will rearrange and simplify to see if it matches the experimental data Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-13 Rearranging the Postulated Rate Eq. Reactive intermediate k Postulated mechanism 1 + 1.) NO O NO 2 3 k 1 k + 2 2.) NO NO 2NO 3 2 1 NO k k C C C O ( ) 2 = + NO r 1 N k C C 2 NO k C k Plug in CNO3 O O 1 + k 2 1 Common denominator 2 N O C 2 NO k C k k ( ) Factor out 1 NO O k C 1 = + NO r 1 NO k C C 1 O C + k 2 1 2 NO 2 + + k k 2 NO k C k C 2 NO k C k k ( ) 1 1 = + NO r 1 NO O k C C Add fraction + 2 NO k C 2 1 2 NO 1 2 ( 1 2 NO 2k k C k C 2 NO 2k C k C + ( ) Multiply O = NO r 1 NO k C C 2 = NO r O k 2 + 2 NO k C 1 2 NO 1 Conventional to reduce the additive constant in the numerator to 1 ) 2 2k k k C C 1 2 1 + 1 k NO C O 2 = NO r ( ) k 2 1 NO Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-14 Comparison Between Postulated and Experimental Rate Equation Reactive intermediate k Postulated mechanism 1 + 1.) NO O NO 2 3 k 1 k + 2 2.) NO NO 2NO 3 2 Compare rate eq for postulated mechanism to the experimental rate eq ( ) 2 2 2k k k C C i NO kC 1 k C + C 1 2 1 + 1 k NO C O O 2 2 = NO r = NO r ( ) k 2 1 NO ii NO Rate equation for postulated mechanism Experimentally observed rate equation Clicker Q: Are these rate equations the same? a) Yes b) No 1 k Yes, these are the same postulated rate law explains the experimental data 2k k k k 1 2 2 = = k k i ii 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-15 Chain Reaction A chain reaction consists of the following sequence: Initiation formation of an active intermediate (radicals) Propagation or chain transfer interaction of an active intermediate with the reactant or product to produce another active intermediate (a radical species) Termination deactivation of the active intermediate Common in radical polymerizations and cracking of ethane Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-16 Free Radical Polymerizations (4 steps) M monomer M M M polymer M-M-M M M n k0 1. Initiation: Initiator (I) decomposes to 2 free radicals 2I 2I ki Radical (1) + I M R 1 kp 2. Propagation: + kp R M R Chain elongation, new monomers add to chain 1 2 + R M R+ j j 1 km 3. Chain transfer: + + R M P R j j 1 Live polymer chain transfers radical to monomer. Polymer chain is no longer reactive (dead). Can also transfer to solvent or other species kadd j k R R + 4b. Termination by disproportionation: 4a. Termination by addition: R+ j k kdis + + R R R R j k j k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-17 PSSH Applied to Thermal Cracking of Ethane The thermal decomposition of ethane to ethylene, methane, butane and hydrogen is believed to proceed in the following sequence: 1,C H r = k1 1 C H k C Initiation: 2 6 C H 2CH 2 6 2 6 3 k2 2,C H r = 2 CH k C C Propagation: + + CH 2 6 C H CH 2 5 C H C H 2 6 2 6 3 3 4 k3 = 3,C H r 3 C H k C + 2 5 C H 2 4 C H H 2 4 2 5 k4 4,C H r = 4 H k C C ( 5 H C H + + 2 5 C H H C H 2 6 2 6 2 6 2 ) 2 k5 2C H 4 10 C H Termination: 5,C H r = k C 2 5 C H 2 5 2 5 (a) Use the PSSH to derive a rate law for the rate of formation of ethylene (b) Compare the PSSH solution in Part (a) to that obtained by solving the complete set of ODE mole balance Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-18 = r k 3 C C The rate of formation of ethylene Goal: replace CC2H5 C H 2 H 4 2 5 The net rates of reaction of reactive intermediates C2H5 , CH3 , H are: C2H5 was formed in rxns 2 & 4, and consumed in rxns 3 & 5: r r r r 1,C H r = 1 C H k C 2 6 2 6 = + + 5,C H r 2,C H r = 2 CH k C C C H 2 5 2,C H 3,C H 4,C H 2 6 2 4 2 6 2 5 C H 2 6 2 6 3 CH3 was formed in rxn 1 and consumed in rxn 2: C = 3,C H -r r -k C H 2 5 3 = + 2 4 CH r H was formed in rxn 3 and consumed in rxn 4: 1,C H 2r 2,C H r 3 2 6 2 6 = 4 H k C C ( 5 4,C H C H 2 6 2 6 ) 2 5,C H r = k C = + H r 3,C H r 4,C H r C H 2 5 2 5 2 4 2 6 Plug rate eqs into eq above, assume rate = 0 (PSSH) & solve for reactive species r C C k C k ( ) 2 = + = k C C k C 0 C H 2 CH3 C H 2 6 3 C H 2 5 4 H C H 2 6 5 C H 2 2 5 5 Need to replace CCH3 and CH = = = CH r 0 1 C H 2k C k C C 1 C H 2k C k 2 C C C 2 CH C H 2 H C H 2 3 2 6 3 6 2 6 3 6 1 C H k C k C k C H C 2k k 3 2 6 1 2 5 = = C C = C Do the same for CH H CH3 CH 4 C H k C 3 2 C H 2 2 6 2 6 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-19 = r k 3 C C The rate of formation of ethylene Goal: replace CC2H5 C H 2 H 4 2 5 The net rates of reaction of active intermediates C2H5 , CH3 , H are (PSSH): C2H5 was formed in rxns 2 & 4, and consumed in rxns 3 & 5: r r r r r 1,C H r = 1 C H k C 2 6 2 6 = + + 2,C H r = 2 CH k C C C H 2 5 2,C H 3,C H 4,C H 5,C H 2 6 2 4 2 6 2 5 C H 2 6 2 6 3 CH3 was formed in rxn 1 and consumed in rxn 2: C = 3,C H -r r -k C H 2 5 3 = + 2 4 CH r H was formed in rxn 3 and consumed in rxn 4: 1,C H 2r 2,C H r 3 2 6 2 6 = 4 H k C C ( 5 4,C H C H 2 6 2 6 ) 2 5,C H r = k C = + H r 3,C H r 4,C H r C H 2 5 2 5 2 4 2 6 Plug rate eqs into eq above, assume rate=0 (PSSH) & solve for reactive species ( ) 2 = + = C r k C C k C k C C k C 0 H 2 CH3 C H 2 6 3 C H 2 5 4 H C H 2 6 5 C H 2 2 5 5 Plug in expressions for CCH3 and CH into C2H5 rate eq for C2H5 & solve for C2H5 assuming rate = 0 (PSSH) k C H C 2k k 3 2 5 = C 1 = CH C H 4 C H k C 3 2 2 6 k k C ( ) 2k k 2 3 C H 2 5 C 1 = + = r k C k C k C k C 0 C H 2 5 2 C H 2 6 3 C H 2 5 4 C H 2 6 5 C H 2 5 2 4 C H 2 6 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-20 = r k 3 C C The rate of formation of ethylene Goal: replace CC2H5 C H 2 H 4 2 5 The net rates of reaction of active intermediates C2H5 , CH3 , H are (PSSH): C2H5 was formed in rxns 2 & 4, and consumed in rxns 3 & 5: r r r r r 1,C H r = 1 C H k C 2 6 2 6 = + + 2,C H r = 2 CH k C C C H 2 5 2,C H 3,C H 4,C H 5,C H 2 6 2 4 2 6 2 5 C H 2 6 2 6 3 CH3 was formed in rxn 1 and consumed in rxn 2: C = 3,C H -r r -k C H 2 5 3 = + 2 4 CH r H was formed in rxn 3 and consumed in rxn 4: 1,C H 2r 2,C H r 3 2 6 2 6 = 4 H k C C ( 5 4,C H C H 2 6 2 6 ) 2 5,C H r = k C = + H r 3,C H r 4,C H r C H 2 5 2 5 2 4 2 6 Plug rate eqs into eq above, assume rate=0 (PSSH) & solve for reactive species k C H C 2k k ( ) 3 2 2 5 1 = C = CH C = + = C r k C C k C k C C k C 0 H H 2 CH3 C H 2 6 3 C H 2 5 4 H C H 2 6 5 C H 2 4 C H k C 3 2 5 5 2 2 6 k C ( ) 2 k k 2 3 C H 2 5 1 + = k C k C k C k C 0 2 C H 2 3 C H 2 5 4 C H 2 5 C H 2 5 6 6 4 C H k C ( C H 2 5 2 2 6 ) ( ) 2 2 = 1 C H 2k C k C + = 1 C H 2k C k C k C k C 0 5 C H 2 5 3 C H 2 5 3 C H 2 5 5 2 6 2 6 1 C H 2k C k 1 C H 2k C k 2 2 6 = C 2 6 = C C H 2 5 C H 2 5 5 5 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-21 = r k 3 C C The rate of formation of ethylene Goal: replace CC2H5 C H 2 H 4 2 5 The net rates of reaction of active intermediates C2H5 , CH3 , H are (PSSH): C2H5 was formed in rxns 2 & 4, and consumed in rxns 3 & 5: r r r r r 1,C H r = 1 C H k C 2 6 2 6 = + + 2,C H r = 2 CH k C C C H 2 5 2,C H 3,C H 4,C H 5,C H 2 6 2 4 2 6 2 5 C H 2 6 2 6 3 CH3 was formed in rxn 1 and consumed in rxn 2: C = 3,C H -r r -k C H 2 5 3 = + 2 4 CH r H was formed in rxn 3 and consumed in rxn 4: 1,C H 2r 2,C H r 3 2 6 2 6 = 4 H k C C ( 5 4,C H C H 2 6 2 6 ) 2 5,C H r = k C = + H r 3,C H r 4,C H r C H 2 5 2 5 2 4 2 6 Plug expressions for reactive species into eq for rC2H4 above k C H C 2k k 1 C H 2k C k 3 1 2 5 = = C CH C 2 6 = C H C H 2 5 4 C H k C 3 2 5 2 6 0.5 The CC2H4 depends on CC2H6. How does CC2H6 change with time? 2kC k 1 = r k 3 C C r = k C H 2 H 2 4 C H 3 2 6 C H 4 2 5 5 Need to eliminate the reactive species -r 1 C H = k C +k C C +k C C 2 6 C H 2 CH 2 6 C H 4 H 2 6 C H 2 6 3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-22 Rate of disappearance -r 1 C H =k C 2 CH +k C C +k C C of ethane: 2 6 C H 2 6 C H 4 H 2 6 C H 2 6 3 Purpose: replace [CH3 ] and [H ] The net rates of reaction of active intermediates CH3 , C2H5 , H are (PSSH): r r r = + = 4,C H r 5,C H r 0 C H 2 5 2r 2,C H 3,C H 2 6 2 4 2 6 r 2 5 = + = = + = 3,C H r 4,C H r 0 CH r 2,C H r 0 H 1,C H 2 4 2 6 3 2 6 2 6 From the previous slide: 12 k C H C 3 2k k = 2 5 CH C 2k k = C 1 = C C 1 2 H 3 4 C H k C 2 5 C H 2 6 C H 5 2 6 12 k k 2 k k 1 3 1 = C H 0.5 C 4 5 2 6 C H 2k k -r 1 C H = k C +k C C +k C C 2 6 C H 2 CH 2 6 C H 4 H 2 6 C H 2 6 3 1 = CH C 3 2 0. 5 C k k 2k k 2k k 2 6 C H 3 1 1 -r 1 C H = k C +k C + k 2 6 C H 2 2 6 C H 4 0.5 2 6 C 2 4 5 2 6 C H 0.5 0.5 2k k 2k k 1 1 -r = 3k C +k C -r 1 C H = k C +2k C +k C 2 6 C H 1 C H 3 2 6 C H 2 6 C H 1 C H 3 2 6 C H 2 6 2 6 2 6 5 5 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-23 12 12 2k k 2k k 1 1 r = k C -r = 3k C +k C 2 4 C H 3 2 6 C H 2 6 C H 1 C H 3 2 6 C H 2 6 5 5 For a constant-volume batch reactor : 12 12 d C H C dt dC 2k k 2k k C H dt 1 1 2 6 2 4 = k C - = 3k C +k C H C 3 2 6 C H 1 C H 3 2 6 2 6 5 5 For given initial concentration of C2H6 and temperature, these two equation can be solved simultaneously ( i.e., use Polymath) Providing the concentration - time relationship using the PSSH Other methods can also be used - solve the complete set of ODE mole balances Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-24 k1 C H 2CH 2 6 3 H C H + + k4 C H H 2 6 2 5 2 + + k2 CH C H CH C H 3 2 6 4 2 5 k5 2C H C H 2 5 4 10 + k3 C H C H H 2 5 2 4 1. Mole balances: (Batch) 2. Rate laws for each species: dC dt dC dt 1 1 r = -k C -k C C -k C C = r 1 C2H6 1 1 2 1 2 4 1 6 2 = r r = 2k C -k C C All these O.D.Es can be solved simultaneously CH3 2 2 1 1 2 2 1 dC dt dC dt dC dt dC dt = r 2 1 2 k C C 3 = r 3 CH4 3 2 r =k C C -k C +k C C -k C 4 =r C2H5 4 2 1 2 3 4 4 1 6 5 4 4 r = k C 5 = r C2H4 The comparisons of the results obtained from the two methods are shown on page 391 of textbook. The two results are identical, indicating the validity of the PSSH under these conditions 5 3 4 5 r = k C -k C C 6 = r H 6 3 4 4 1 6 6 dC dt dC dt r = k C C 7 H2 = r 7 4 1 6 1 k C 2 7 2 C4H10 8 r = = r 8 5 4 8 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-25 Ozone (O3 ) Example Problem Overall Reaction for Ozone Decomposition: 2O 3O 3 2 When ozone decomposes in the presence of an inert gas, M, the following kinetics are observed: 2 kC C C k'C O M 3 = O r + C 3 O M O 2 3 Postulate a reaction mechanism that is consistent with this rate law This is provided as an extra example that can be skipped if there isn t enough time to cover it in class. Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Postulating Mechanism for O3 Decomposition (Step 1) 1. If CB appears in the denominator of the rate law, then one elementary rxn step is probably: * B A Collision products + 2. If the denominator contains a constant term, then one rxn step is probably: * A Decomposition products 3. If the numerator contains a species concentration, then one rxn step is probably: species C other species? + L10-26 reactive intermediate * + A other products? 2 kC C C k'C Experimentally observed rate equation for O M Apply: 3 = O r ( ) + overall reaction : 2O 3O C 3 3 2 O M O 2 3 CO2, CM & CO3 in denominator, so O2, M, and O3 must each collide a with reactive intermediate. What is the reactive intermediate? Since one oxygen atom is lost from the ozone molecule (O3), oxygen radicals (O ) are likely the reactive intermediate: + 2 O O n 1) 3 O + + + M O M ? (PR3) O 3 (Possible Rx O 2O (PR2) 2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Postulating Mechanism for O3 Decomposition (Step 1 continued) L10-27 1. If CB appears in the denominator of the rate law, then one elementary rxn step is probably: * B A Collision products + reactive intermediate 2 kC C C k'C Experimentally observed rate equation for O M Apply: 3 = O r ( ) + overall reaction : 2O 3O C 3 3 2 O M O 2 3 CO2, CM & CO3 in denominator; they must collide with reactive intermediate O + 2 O O O n 1) + 3 O O 3 (possible rx 2O (PR2) + + M O M ? (PR3) 2 Wait, M is inert, so it cannot react with O to create a new chemical species An inert molecule can provide kinetic energy in another reaction M must participate in one of the other reactions Which one? CM is multiplied by CO2 in the denominator, so combine PR3 with PR1 + + + M O O O M (P R1b) 2 3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Postulating Mechanism for O3 Decomposition (Steps 2 & 3) 1. If CB appears in the denominator of the rate law, then one elementary rxn step is probably: * B A Collision products + 2. If the denominator contains a constant term, then one rxn step is probably: * A Decomposition products 3. If the numerator contains a species concentration, then one rxn step is probably: species C other species? + L10-28 reactive intermediate * + A other products? 2 kC C C k'C + M Experimentally observed rate equation for O M Apply: 3 = O r ( ) + overall reaction : 2O + 3 O 3O PR2) C O 3 3 2 ( O 2 O M O O (P 2 3 + + M O R1b) O 2 2 3 Denominator doesn t contain a constant, so step 2 isn t in our mechanism Both CO3 and CM appear in the numerator, so one reaction step may be: + + 3 O M M O Note that PR4 is the reverse of PR1 + O ( PR4) 2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-29 Postulated Mechanism for Ozone Decomposition 2 O M O O M O C C k'C kC C Experimentally observed rate equation for Apply: 3 = r ( ) overall reaction : 2O 3O + 3 3 2 2 3 + + + + + M O O O M CM and CO2 in denominator: CO3 in denominator: CO3 and CM in numerator: 2 3 O + O M 2O O Reactive intermediate 3 2 + O M O 3 2 k1 k1 + + + Postulated mechanism: O M M O O 3 2 Does this add up to the overall reaction? + k2 + O O 2O 3 2 2O 3O yes! 3 2 Now derive a rate equation for the postulated mechanism and check if it describes the experimentally observed rate equation Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-30 Postulated Mechanism for Nonelementary Reaction Kinetics 2 O M O O M O C C k'C intermediates k1 3 k1 + 3 O O Write rO3 for the postulated reaction mechanism Nonelementary kinetics, result of multiple elementary rxns & active kC C 3 = r + 3 2 3 Reactive intermediate + + + Postulated mechanism: O M M O O 2 k2 2O 2 ( ) ( ) = O r rxns that consume O - rxns that form O 3 3 3 = + O r 1 O k C C 1 M O k C C C k C C M O 2 O O 3 3 2 3 -rO3 is in terms of CO , which is not measurable species because it is a reactive intermediate (so reactive it is consumed as fast as it is formed) Need to get CO in terms of measurable species and plug into rO3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-31 Pseudo-Steady State Hypothesis k 3 k + 3 2.) O O = 3 3 2 O 1 O M 1 M O O ( 3 3 O 1 O M Reactive intermediate, must replace CO in the rate equation 1 + + + 1.) O M M O O Postulated mechanism: 2 1 k 2 2O 2 + r k C C k C C C 2 O k C C Factor out to simplify ) 2 1 M O O O 3 = + r k C C 2 O k C k C C C 3 Write rO Rearrange to get CO in terms of measurable species plug eq for CO back into rO3 = 3 O 1 O M 1 M CO is very small, and O is so reactive that it is consumed as fast as it is formed, so apply pseudo-steady state hypothesis: 1) 2) 3) r k C C k C C C k C C O O 2 O O 2 3 O r 0 ( ) = O r = + 0 1 O k C C C 1 M O k C C k C M O 2 O 3 2 3 Put concentration of reactive intermediate O in terms of other species Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-32 Concentration of Reactive O Postulated mechanism: + 3 1.) O M Reactive intermediate, must replace CO in the rate equation k 1 + + M O O 2 k 1 k + 2 2.) O O 2O 3 2 2 kC C C k'C Observed rate equation (nonelementary) O M 3 = O r + C 3 O M O 2 3 ( ) = + O r 1 O k C C 2 O k C k C C C M 1 M O O 3 3 3 2 ( ) Solve for CO in terms of other species = O r = + ) 0 1 O k C C C 1 M O k C C k C M ( O 2 O 3 2 3 + = 1 M O k C C 2 O k C C 1 O k C C O M 2 3 3 1 O k C C M k C 3 = C Plug CO into rO3 O + 1 M O k C C 2 O 2 3 1 O k C C ( ) M k 3 = + O r 1 O k C C k C k 1 M C C M 2 O O + 1 M O k C C C 3 3 3 2 2 O 2 3 Now we will rearrange and simplify to see if it matches the experimental data Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-33 Rearranging the Postulated Rate Eq. Postulated mechanism: k + 3 2.) O O Reactive intermediate, must replace CO in the rate equation k 1 + + + 1.) O M M O O 3 2 1 k 2 2O 2 1 O k C C ( ) M k C 3 = + O r 1 O k C C k C 1 M O k C C Plug in CO M 2 O + 1 M O k C C 2 O C k C 3 3 3 2 2 O 2 3 2 1 2 k k C C 1 1 M k k C C Multiply out brackets Get common denominator O k C C ) 3 O M O 3 2 3 = + O r 1 O k C C M + 3 3 1 M O 2 O 2 3 ( 2 2 + 1 O k C C k C C k C 1 2 k k C C 1 1 M k k C C C M 1 M O k C 2 O k C C M O O 3 2 3 2 3 = + O r + + 1 M O k C C C k C 3 2 2 O 1 M O 2 M C 2 O 2 2 3 2 k k C 3 C 2 + + k k C C k k C C 1 2 k k C k C 1 1 M O O 1 2 O M O 1 1 M O O 2 3 3 3 2 3 = O r + k C C C 3 1 M O 2 O 2 3 2 2k k C C k C ( ) 2 Conventional to remove constant from 1st term 2k k C C k C C C 1 2 O M 3 = 1 2 1 k O M O r 3 = O r + k M O C C 3 ( ) + k 3 1 2 O 2 3 M O 2 1 O 2 3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L10-34 Comparison Between Postulated and Experimental Rate Equation Postulated mechanism: k + 3 2.) O O Reactive intermediate, cannot appear in the rate equation k 1 + + + 1.) O M M O O 3 2 1 k 2 2O 2 Compare rate eq for postulated mechanism to the experimental rate eq ( ) 2 2 kC C C k'C 2k k k C C C O M 1 2 1 k O M 3 3 = = O r O r ( ) + + C M O C C k 3 3 O M O 2 1 O 2 3 2 3 Rate equation for postulated mechanism Experimentally observed rate equation 2k k k k k 1 2 2 = = k k' 1 1 These are the same postulated rate law explains the experimental data Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
